Многоспиральные вихри

Коллективом ученых из Института теплофизики им. С.С. Кутателадзе СО РАН и Технического университета Дании впервые показаны и экспериментально исследованы устойчивые конфигурации самоорганизующихся вихревых мультиплетов в закрученном потоке жидкости, генерируемом в полости цилиндра его вращающимся торцом

Исследование поведения равновесных когерентных конфигураций нескольких вихрей (вихревых мультиплетов) ведется в фундаментальных и прикладных целях с XIX в. Сегодня вопрос о структуре подобных образований имеет принципиальное значение как для развития вихревой концепции теории турбулентности, так и для анализа сложных процессов в интенсивно закрученных потоках, возникающих в природе и различных технических устройствах.

Теория точечных вихрей предсказывает существование до семи вихрей в равновесных круговых конфигурациях; ее обобщение на винтовые вихри снижает прогноз до шести.

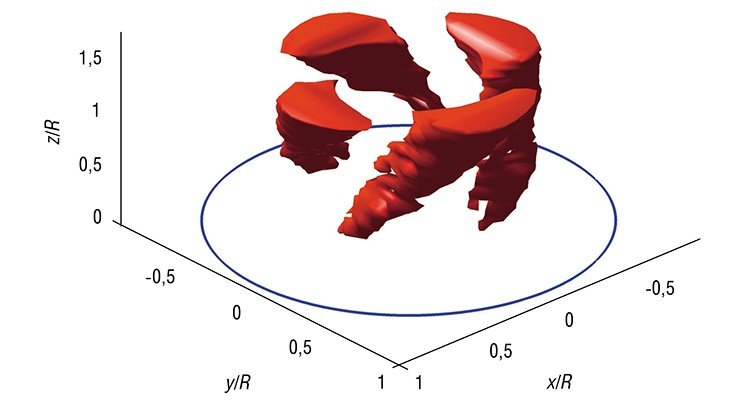
Однако определить пространственные структуры вращающихся вихревых мультиплетов в реальных условиях очень сложно: до недавнего времени удалось получить экспериментальные данные только о структуре дуплетов (двуспиральных или двойных вихрей). Визуализировать более сложные мультиплеты не удавалось. Исключением можно считать трассировку концевых вихрей, сходящих с лопастей вращающейся турбины или пропеллера.

Вихревые мультиплеты образутся при распаде одиночного вихря. Поэтому экспериментальное изучение этого процесса важно не только для понимания природы самого явления, но и для исследования различных вихревых конфигураций. Именно таким образом ранее были исследованы вихревые дуплеты.

Визуализировать процесс распада вихря, образующегося в сосуде с жидкостью, можно в условиях лабораторного опыта с помощью красителя. Распад концентрированного вихря характеризуется резким замедлением скорости по его оси, иногда приводящим к образованию зоны обратного течения (рециркуляции). Этот процесс можно отследить благодаря захваченному вихрем красящему веществу, которое первоначально распределено строго вдоль вихревой оси.

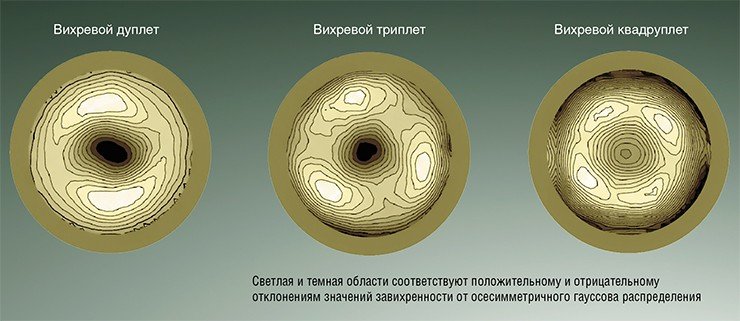
В рамках совместной работы сибирских и датских ученых была проведена серия экспериментов, направленная на выявление пространственной структуры устойчивых мультиплетных форм распада вихря. В работе были использованы две однотипные экспериментальные установки, представляющие собой круговые цилиндры с вращающимся торцом и отличающиеся только размерами и рабочими жидкостями. Характеристики закрученного потока, получаемого в них при вращении торца, определяются двумя режимными параметрами: отношением высоты цилиндра к радиусу основания и числом Рейнольдса, связанным с угловой скоростью вращения торца и вязкостью рабочей жидкости. В экспериментах были использованы цилиндры с диаметрами 5,6 и 30 см, содержащие дистиллированную воду и 75 %-ю водно-глицериновую смесь соответственно.

Прямое сопоставление визуальных картин течения, полученных на обеих установках, позволило установить, что при одинаковых значениях режимных параметров в них реализуются одни и те же режимы распада вихря с устойчиво воспроизводимыми вихревыми мультиплетами. Неслучайный характер полученных визуализаций подтверждается и исследованием трехмерного поля скорости, построенном с помощью стереоскопической системы цифровой трассерной визуализации 3D PIV на режимах получения устойчивых вихревых образований. Это исследование позволило не только определить начало перехода от осесимметричного течения к режиму с равновесно вращающимися мультиплетами, но и четко идентифицировать возникающую вихревую структуру.

С прикладной точки зрения, важность существования такого явления, как распад вихря с образованием вихревых мультиплетов, весьма велика. Оно может стать отправной точкой для описания отдельных режимов работы вихревых установок, создания концепции многоячеистого облакообразования в центре интенсивных тропических циклонов, а также моделирования торнадо с мультивихревой структурой ядра.

К. т. н. И. В. Наумов (Институт теплофизики
им. С. С. Кутателадзе СО РАН, Новосибирск),
д. ф.-м. н. В. Л. Окулов (Технический университет Дании, Копенгаген)

Литература

Okulov, V. L. On the stability of multiple helical vortices // J. Fluid Mech. 2004. V. 521. P. 319—342.

Окулов В. Л., Наумов И. В., Соренсен Ж. Н. Самоорганизующиеся вихревые мультиплеты в закрученном течении // Письма в ЖТФ. 2008. Т. 34, № 15. С. 89—95.

Наумов И. В., Окулов В. Л., Соренсен Ж. Н. Применение 3D PIV для диагностики самоорганизующихся вихревых мультиплетов // Оптические методы исследования потоков: Труды 10-й Международной научно-технической конференции. Москва, 23—26 июня 2009 г. М.: Изд. МЭИ, 2009. С. 342—345.