: 25 апр 2013 , Полеты в виртуальности и наяву , том 49, №1

Обратные задачи естествознания и компьютерное моделирование

С точки зрения соотношения причина-следствие, все задачи математического моделирования условно делятся на два больших класса: прямые задачи и обратные. В первом случае при известных причинах требуется определить следствия, во втором случае, естественно, наоборот: найти причины, приведшие

к тем или иным следствиям. Первые публикации по обратным и некорректным задачам, появившиеся в середине XX века, были связаны с различными разделами естествознания: физикой (квантовой теорией рассеяния, электродинамикой, акустикой), геофизикой (электроразведкой, сейсмикой, магниторазведкой), астрономией и др. С появлением же мощных ЭВМ область приложений обратных и некорректных задач охватила практически все научные дисциплины, где используются математические методы, включая медицинскую и промышленную томографию, дефектоскопию и т. п.

Прежде чем говорить об обратных задачах, необходимо определить, что такое прямые задачи. В прямых задачах математической физики исследователи стремятся найти (в явной форме или приближенно) функции, описывающие различные физические явления (например, распространение звука, сейсмических колебаний, электромагнитных волн и т. п.). Эти функции являются решениями уравнений математической физики, для которых необходимо задать коэффициенты уравнения, начальные и граничные условия.

Однако свойства среды на практике довольно часто сами являются неизвестными. А это означает, что нужно формулировать и решать обратные задачи, где требуется определить либо коэффициенты уравнений, либо неизвестные начальные или граничные условия, либо местоположение, границы и другие свойства области, в которой идет исследуемый процесс.

Ясно, что для решения обратной задачи необходимо иметь дополнительную информацию (например, значения решения внутри области или на ее границе, спектральные либо кинематические характеристики процесса и т. п.). Эти задачи в большинстве случаев некорректны, т. е. в них нарушено хотя бы одно из трех свойств корректности – условие существования, единственности и устойчивости решения по отношению к малым вариациям данных задачи.

Искомыми функциями в обратных задачах являются, как правило, плотность, электропроводность, теплопроводность, скорость распространения волн и другие важные свойства исследуемой среды. В некоторых обратных задачах требуется найти местоположение, форму и структуру включений, дефектов либо источников тепла, колебаний, напряжения, загрязнения и т. п. Неудивительно, что при таком широком наборе приложений теория обратных и некорректных задач с момента своего появления стала одной из наиболее стремительно развивающихся областей современной науки.

Об определении обратных задач

Каждый человек в своей повседневной жизни ежеминутно решает обратные и некорректные задачи. И делает это, как правило, быстро и эффективно.

Возьмем, к примеру, зрительное восприятие. Установлено, что за минуту мы фиксируем лишь конечное число точек окружающего мира. Мозг, как мощный персональный компьютер, по этим точкам восполняет (интерполирует и экстраполирует) все, что глаз не успел зафиксировать. И, несмотря на сильную некорректность (неединственность и неустойчивость решения) этой обратной задачи, мозг решает ее довольно быстро. Ясно, что воссоздать таким способом истинную картину, да еще объемную и цветную, можно лишь в случае, если мы с ней уже более-менее знакомы: мозг использует богатый опыт (априорную информацию).

Вообще, если мы хотим понять что-то достаточно сложное – решить задачу, вероятность ошибки в которой достаточно велика, мы, как правило, приходим к неустойчивой (некорректной) задаче. Каждый знает, как легко ошибиться, пытаясь восстановить прошлое по некоторым фактам из настоящего: проследить мотивы и детали преступления по имеющимся уликам, понять причины зарождения болезни по результатам обследования и т. п. Или заглянуть в будущее – предвидеть жизненный путь ребенка, направление развития страны и другие сложные процессы. Так же трудно проникнуть в зону недоступности и понять, что, к примеру, происходит во внутренних органах человека, или где находится месторождение полезных ископаемых и т. д. В сущности, любая попытка расширить границы непосредственного (чувственного, зрительного, слухового и т. п.) восприятия окружающего мира приводит к некорректным задачам.

Обратные и некорректные задачи объединяет одно важное свойство – неустойчивость решения по отношению к малым ошибкам измерений данных. В большинстве интересных случаев обратные задачи являются некорректными, а некорректные задачи, как правило, можно сформулировать как обратные по отношению к некоторым прямым (корректным) задачам. Но поскольку исторически обратные и некорректные задачи формулировались и изучались довольно часто независимо и параллельно, сейчас в научной литературе используются оба этих термина.

Суммируя вышеизложенное, можно сказать, что специалисты по обратным и некорректным задачам занимаются исследованием свойств и методов регуляризации неустойчивых задач, создают и изучают устойчивые методы приближения неустойчивых отображений.

В высшем образовании теория обратных и некорректных задач становится одним из наиболее эффективных средств изложения естественно-научных дисциплин по ряду причин.

Во-первых, эта теория наиболее полно отвечает принципу интеграции наук, объединяя на основе математических уравнений все основные направления естествознания, что позволяет эффективно использовать в образовании междисциплинарный подход. Студенты, изучая курс обратных и некорректных задач, заново «проходят» практически все изученные ранее дисциплины, глубже проникают в их математические особенности и взаимосвязи. Во-вторых, изучение теории обратных и некорректных задач приводит к новому пониманию роли математики в обществе, а также внутреннего единства и красоты самой математики. Наконец, изучение этой теории позволяет глубже осознать роль моделирования в процессе познания человеком окружающего его мира.

Немного истории

Многие математические понятия и задачи возникали в результате исследования тех или иных физических процессов или явлений, и это особенно справедливо для обратных и некорректных задач. Философское утверждение Платона о том, что человеку в процессе познания доступны только тени на стене пещеры и эхо (данные обратной задачи), стало предвестником решенной Аристотелем задачи восстановления формы Земли по ее тени на Луне (обратной задачи проективной геометрии).

Введение физического понятия мгновенной скорости привело Ньютона к открытию производной, а проблема неустойчивости (некорректности) задачи численного дифференцирования функции, заданной приближенно, актуальна и по сей день. Исследования лорда Рэлея по акустике побудили его сформулировать вопрос о возможности нахождения плотности неоднородной струны по ее звучанию (обратная задача акустики), что предвосхитило развитие сейсморазведки, с одной стороны, и развитие теории спектральных обратных задач, с другой. Изучение движения небесных тел и задача оценки неизвестных величин по результатам измерений, содержащим случайные ошибки, привело Лежандра и Гаусса к переопределенным системам алгебраических уравнений и к созданию метода наименьших квадратов. Коши предложил метод наискорейшего спуска для нахождения минимума функции нескольких переменных. В 1948 г. Л. В. Канторович обобщил, развил и применил эти идеи к операторным уравнениям в гильбертовых пространствах.

Но хотя отдельные обратные и некорректные задачи с давних пор и были объектом внимания самых разных исследователей, математические особенности некорректных задач были сформулированы Адамаром лишь вначале XX века. Пример некорректности задачи Коши для уравнения Лапласа, приведенный Адамаром, породил сомнения в целесообразности исследования некорректных задач. Тезис о том, что «некорректных задач нет, а есть задачи плохо поставленные», одних исследователей охлаждал, а других, напротив, побуждал искать новые пути к их решению.

Например, в середине прошлого века Р. Курант исследовал некорректную задачу восстановления функции по ее сферическим средним. А выдающийся отечественный математик С. Л. Соболев стал научным консультантом докторской диссертации В. К. Иванова «Исследования по обратной задаче теории потенциала», давшей теоретическое обоснование решения обратной задачи гравиразведке, используемой для исследования литосферы и поиска полезных ископаемых.

Невозможно рассказать обо всех аспектах теории обратных задач и ее приложений. Упомянем лишь два направления, существенный вклад в зарождение и развитие которых внесли ученые, работавшие в новосибирском Академгородке – В. Е. Захаров и А. Б. Шабат (метод обратной задачи рассеяния), А. С. Алексеев и С. В. Гольдин (обратные задачи геофизики). Метод обратной задачи рассеяния был применен для решения нелинейных уравнений математической физики (уравнение Кортевега-де Фриза, нелинейное уравнение Шредингера, уравнение Кадомцева-Петвиашвили и др.) и стимулировал новые исследования в различных областях математики и физики (спектральная теория дифференциальных операторов, классическая алгебраическая геометрия, релятивистские струны и др.). Метод обратной задачи рассеяния называют жемчужиной математической физики ХХ века. Результаты А. С. Алексеева и С. В. Гольдина по применению в геофизике спектральной теории обратных задач и интегральной геометрии стали теоретической основой многих геофизических методов (обратные кинематические и динамические задачи сейсмики). Отметим, что признанные успехи нынешнего поколения сибирских геофизиков во многом определены их высокой математической подготовкой на геолого-геофизическом факультете НГУ. Автору статьи посчастливилось работать на кафедре геофизики в те годы, когда там был создан творческий союз преподавателей геофизиков (С. В. Гольдин, Л. А. Табаровский, М. И. Эпов, Ю. А. Дашевский и др.) и математиков (М. М. Лаврентьев, А. С. Алексеев, В. Г. Романов, Т. А. Годунова и др.). Обсуждения того, как надо математику и в каком объеме давать геофизикам, регулярно проводились на собраниях преподавателей, а споры часто напоминали дискуссии на научных конференциях.

Огромный вклад в создание основ теории обратных и некорректных задач внесли наши всемирно признанные соотечественники А. Н. Тихонов, В. К. Иванов и М. М. Лаврентьев. Одна из главных идей состояла в том, что при исследовании некорректных задач необходимо сузить класс возможных решений. При этом важнейшую роль играет выбор множества (множество корректности), в котором ищется приближенное решение. Чаще всего такое множество выбирают компактным, что дает возможность обосновать сходимость регуляризирующих алгоритмов, помогает выбрать параметр регуляризации и оценить уклонение приближенного решения от точного решения некорректной задачи.

Компьютерное моделирование дыхания и торнадо, кровообращения и цунами

Сегодня область применения теории обратных задач крайне широка – при вводе ключевых слов «inverse problems» поисковая системе Google выдает 10 млн ссылок! В качестве примера приведем лишь некоторые из направлений работ сотрудников отдела математических задач геофизики Института вычислительной математики и математической геофизики СО РАН, которые проводятся совместно с научными коллективами из ряда институтов СО РАН, а также с исследователями из Москвы, Астаны, Алматы и Семипалатинска.

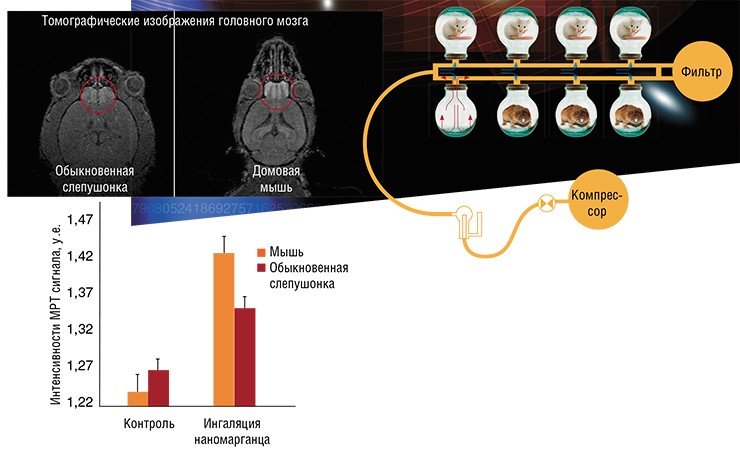
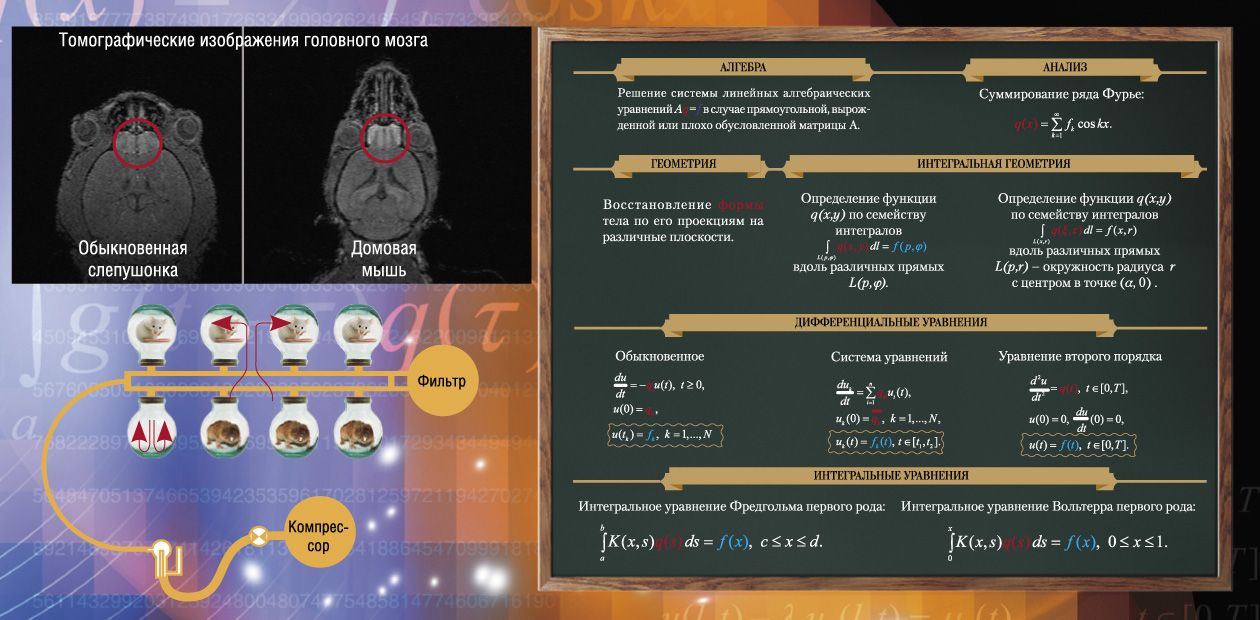
Среди этих работ – исследования двух, на первый взгляд, очень далеких друг от друга процессов: распространения смерча в урочище Медео (Алматы, 17 мая 2011 г.) и процесс поступления наночастиц из носовой полости в мозг при их вдыхании в эксперименте на лабораторных мышах. В первом случае нужно выявить причины возникновения небывалого по мощности смерча, который как спички повалил огромные ели на всем протяжении ущелья. Пока имеются только предположения, что большую роль в его появлении сыграло уникальное сочетание погодных условий, а также возведение каскада высотных зданий, перекрывших естественное движение холодного воздуха вниз по ущелью. Во втором случае мы имеем дело с важной проблемой, связанной с созданием массовых производств нанопрепаратов. Изучение млекопитающих, в разной степени приспособленных к вдыханию пыли, является перспективным подходом к исследованию природных механизмов защиты организма от наноаэрозолей.

Опасной аномалией сосудов головного мозга является артериовенозная мальформация – непосредственное соединение артериальной сети с венозной в виде хаотического клубка перерожденных сосудов. На этом участке кровеносной сети отсутствуют капилляры, поэтому мозг «обкрадывается» – он не снабжается кислородом и питательными веществами. Происходит нарушение параметров кровотока: скорость крови в сосудах резко повышается (до 1,5 м/с), давление в артерии падает, а в вене повышается. Эти процессы могут привести к кровоизлиянию из аномального сосуда.

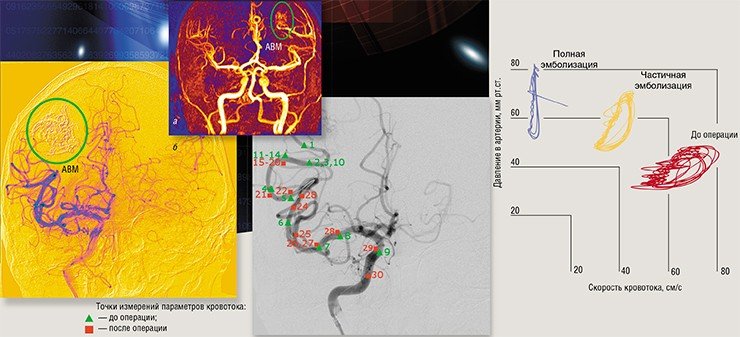
Современный метод лечения артериовенозной мальформации – эмболизация (заклейка). Врач подводит катетер по сети сосудов, стартуя с бедренной артерии, и подает в нее специальный клей, заполняя им хаотический сосудистый клубок Тем самым восстанавливается нормальный кровоток по здоровым сосудам в обход «выключенного» патологического узла.
Сегодня появилась возможность виртуального моделирования хода операции и активного использования хирургами результатов моделирования в реальном режиме времени, непосредственно во время операции. Построение такой модели церебральной гемодинамики при наличии сосудистых аномалий является новым приложением теории обратных задач.
Решить эту задачу удалось в результате совместных усилий медиков из нейрохирургического центра Новосибирского НИИ патологии кровообращения им. акад. Е. Н. Мешалкина и ученых Института гидродинамики СО РАН (Новосибирск). На основе клинических данных по измерениям давления и скорости кровотока в сосудах головного мозга была построена математическая модель – дифференциальное уравнение, описывающее процесс операции

Современные методы вычислений позволяют моделировать оба эти процесса. Правильно задав начальные и граничные условия для соответствующих уравнений газовой динамики, можно приступать к решению обратных задач – восстановления формы источника торнадо, обнаружения мест возможного скопления наночастиц и т. п.

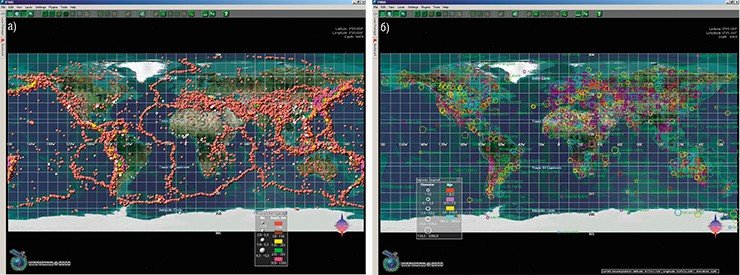
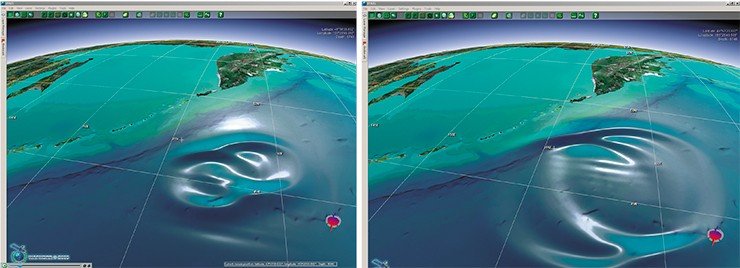
В СО РАН накоплен также большой опыт применения математического моделирования для исследования цунами – одного их самых катастрофических природных явлений, прежде всего в ИВТ СО РАН (Ю. И. Шокин, Л. Б. Чубаров) и ИВМиМГ (В. К. Гусяков, Ан. Г. Марчук). Проблема моделирования этих процессов очень важна, поскольку число таких разрушительных катастроф увеличивается с каждым десятилетием. Особенно значимы задачи оперативного прогнозирования, благодаря которому можно уменьшить число человеческих жертв.

В отделе математических задач геофизики ИВМиМГ разработана специализированная система ITRIS для предупреждения, анализа, оценки риска и последствий природных и техногенных катастроф. Концепция ITRIS базируется на принципах ГИС-технологий и объединяет в своем составе специализированные базы данных, программные компоненты для моделирования опасных природных явлений, инструменты для обработки и анализа геологических данных, включая спутниковые снимки, цифровые модели суши и морского дна, материалы дистанционного зондирования, базы данных по катастрофам, населению и инфраструктуре крупных городов.

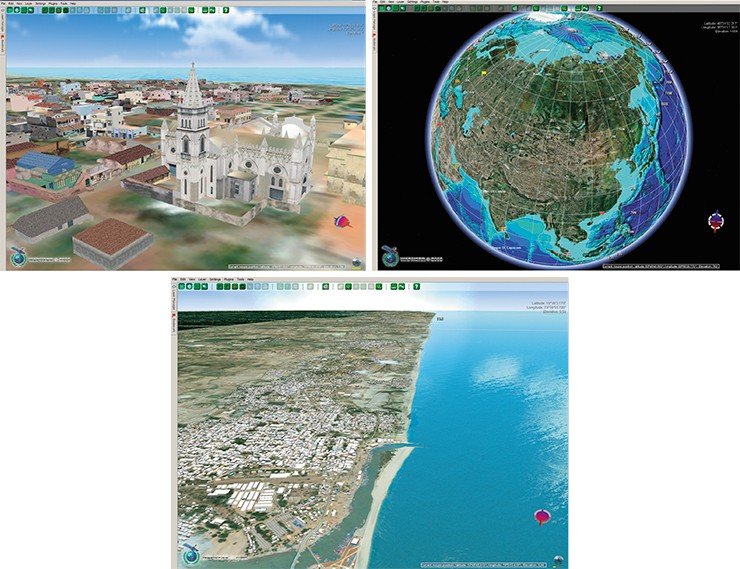
Главное достоинство этой системы – возможность пополнения новыми данными, численными моделями и алгоритмами. Другими словами, система ITRIS позволяет подключать различные модули, реализующие математические модели природных и техногенных катастроф, а также любых других физических процессов.

Без права на ошибку

Популярность обратных задач растет пропорционально мощности компьютеров, поскольку одним из самых доступных и понятных прикладникам методов решения обратных задач является метод подбора (метод палеток). Имея надежный численный метод решения прямой задачи (а значит, достаточно адекватную модель изучаемого явления), исследователь может решать обратную задачу, целенаправленно меняя интересующие его параметры модели. С появлением суперкомпьютеров открываются возможности использовать градиентные методы, стохастические алгоритмы, изучать и применять генетические алгоритмы и нейронные сети.

С появлением ЭВМ математика, по словам основоположника отечественного математического моделирования А. А. Самарского, приобрела свойство экспериментальной науки. Это свойство становится особенно важным благодаря активному вторжению суперкомпьютерных технологий в нашу жизнь. Уже сейчас можно хранить в «облаке», а при определенном навыке и обрабатывать свои файлы, имея при себе лишь небольшой персональный компьютер с выходом в интернет. Мы можем не только покупать практически любые товары и получать любые консультации, включая юридические и медицинские, но и оперативно решать большие задачи по математическому моделированию.

Но наряду с неограниченным ростом «цифровых» возможностей увеличивается и вероятность появления ошибок. По мнению известного отечественного математика С. К. Годунова, в компьютерном моделировании надвигается «экологическая катастрофа». Дело в том, что при выполнении даже элементарных машинных операций (умножения, деления) результат содержит ошибку вычисления, которая возрастает с увеличением количества машинных команд в алгоритме. А, к примеру, моделирование образования только одного белка методами молекулярной динамики потребуется около 10²⁵ машинных команд!

Научиться контролировать ошибки в вычислениях жизненно важно. Поэтому уже сейчас ведутся работы по оптимизации моделей, созданию специальных алгоритмов для архитектуры параллельных систем, по учету и анализу ошибок вычислений. Например, в Японии при создании 10-петафлопсного суперкомпьютера одновременно создавался компьютер-дублер на графических платах, на котором должны отрабатываться программное обеспечение и исследоваться особенности параллельных алгоритмов.

Для отечественной науки наступило время серьезных перемен, которые диктуются не только изменяющимися экономическими условиями, но и внутренней логикой развития системы накопления и преумножения знаний человечества об окружающем мире, о внутреннем строении материи и сознания. Одной из важнейших становится задача сохранить и передать новому поколению накопленный «золотой фонд» российской науки. Одним из путей выхода из кризиса является концентрация усилий и средств на наиболее перспективных направлениях, естественно вытекающих из достижений советских ученых.

Основы теории обратных и некорректных задач были заложены в СССР еще в середине XX в., однако последние десятилетия российская школа стала утрачивать лидирующие позиции в этой области. Много наших способных специалистов, особенно молодых, теперь работают за рубежом. И если в мире издано уже свыше 14 тыс. книг, в названии которых стоит словосочетание «обратные задачи», то в России такие книги появляются не так часто. Тем не менее теория и численные методы решения обратных и некорректных задач естествознания и теперь являются одним из наиболее приоритетных направлений российской науки.

Если государство не сможет поддержать развитие всех направлений, то рано или поздно ему придется выбирать. В этом отношении у специалистов по обратным задачам очень хорошие перспективы. С одной стороны, есть большая и активная когорта маститых ученых, которые уже внесли весомый вклад в развитие теории и создание практических приложений в этой области. С другой – как показывает опыт проведения ежегодной молодежной школы-конференции в новосибирском Академгородке, в нее вовлекается все больше молодых российских математиков, физиков, химиков, геофизиков, биологов и представителей других естественно-научных дисциплин. И это закономерно, ведь стремительно растущие вычислительные мощности превращают обратные задачи в необходимый инструмент не только для исследования уже существующих математических моделей, но и для создания новых моделей, для вывода новых уравнений и закономерностей и для исследования их устойчивости и адекватности.

Литература

Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. Третье изд. М.: Наука, 1986.

Лаврентьев М. М., Романов В. Г., Шишатский С. П. Некорректные задачи математической физики и анализа. Новосибирск: Наука, Сиб. отд-ние, 1980.

Иванов В. К., Васин В. В., Танана В. П. Теория линейных некорректных задач и ее приложения. М.: Наука, 1978.

Кабанихин С. И. Обратные и некорректные задачи. Новосибирск: Сиб. науч. изд-во, 2008.

Koptyug I. V. , Kabanikhin S. I., Sagdeev R. Z. , Parmon V. N. et al. A quantitative NMR imaging study of mass transport in porous solids during drying // Chemical Engineering Science. Pergamon 2000. V. 55. P.1559—1571.

M. P. Moshkin, I. V. Koptyug, R. Z. Sagdeev V. V. Fomin V. M. et al. Adaptation to underground life protects lung and brain from inhaled dust. (to appear).

Эпов М. И., Миронов В. Л., Музалевский К. В., Кабанихин С. И. Применение метода дискретных источников для расчёта полей СШП импульсного электромагнитного дипольного зонда в средах нефтегазового коллектора // Изв. вузов. Физика, 2010. №9/3. С. 257—262.

А. П. Чупахин, А. А. Черевко, А. К. Хе, Н. Ю. Телегина, А. Л. Кривошапкин, К. Ю. Орлов, В. А. Панарин, В. И. Баранов. Измерения и анализ церебральной гемодинамики у больных с сосудистыми мальформациями головного мозга // Патология кровообращения и кардиохирургия. 2012. № 4. С. 27—31.

Ilyin A., Kabanikhin S. I., Nurseitov D. B. et al. Analysis of ill-posedness and numerical methods of solving a nonlinear inverse problem in pharmacokinetics for the two-compartmental model with extravascular drug administration // Journal of Inverse and Ill-Posed Problems. 2012. V. 20, N. 1. P. 39—64.

: 25 апр 2013 , Полеты в виртуальности и наяву , том 49, №1