Со скоростью звука
Пассажирские магистральные самолеты со сверхзвуковой скоростью сегодня не летают. Как выяснилось, «сверхзвуковые» проекты ТУ-144 и Конкорд оказались экономически не выгодными. Первая попытка преодолеть звуковой барьер в мирных целях оказалась неудачной, так как при приближении к звуковому барьеру резко возрастает лобовое сопротивление самолета и уменьшается подъемная сила. Итак, «сверхзвука» нет, а что же есть? Есть «трансзвук».
Трансзвуковые скорости — это диапазон скоростей чуть больше и чуть меньше скорости звука (примерно от 0,8 до 1,2 скорости звука). Этот термин пришлось ввести для описания пограничного режима обтекания тела, когда часть обтекающего потока становится сверхзвуковой, а часть потока так и остается в дозвуковом режиме...
С чего все начиналось
Работы по увеличению скорости полета и аэродинамического качества самолетов были начаты еще в 30-х гг. прошлого столетия. А на рубеже 30-40-х гг. двадцатого века удалось экспериментально доказать, что с увеличением скоростей полета сопротивление крыльев и других частей самолета резко возрастает. Также непредсказуемо меняются подъемная сила и момент крыла. Было установлено, что данные феномены связаны с тем, что в потоке появляются области, в которых воздух движется относительно обтекаемого тела со скоростью, превосходящей скорость звука. Скорость самолета, при которой у его поверхности появляются сверхзвуковые потоки, назвали критической.
Теоретические представления о подъемной силе крыла и о силах сопротивления при докритических скоростях сложились под влиянием идей выдающегося русского ученого, создателя аэродинамики Н. Е. Жуковского: крыло обладает подъемной силой за счет того, что скорость, а следовательно, и разрежение (уменьшение давления) у верхней поверхности больше, чем у нижней. Величина подъемной силы равна разности давлений на нижней и верхней поверхностях крыла. Сопротивление крыльев бесконечного размаха складывается из сопротивления трения и лобового сопротивления, возникающего из-за неполного восстановления давления в хвостовой части крыла. При обтекании крыльев идеальным газом эти сопротивления отсутствуют. У крыла конечного размаха появляется еще и так называемое, индуктивное сопротивление, непосредственно связанное с наличием подъемной силы.
Однако этих классических представлений оказалось недостаточно, чтобы объяснить явления, которые наблюдаются при скорости полета, превышающей критическую. Невыясненной осталась и физическая причина совпадения момента роста сопротивления и появления у поверхности крыла сверхзвуковой скорости.
К тому моменту, когда проблемы, возникающие при критических скоростях, были осознаны, в мире уже велись исследования, связанные с учетом влияния сжимаемости (уменьшение плотности газа при увеличении скорости течения) на распределение давления по поверхности крыла. Так, одним из авторитетных специалистов по аэродинамике того времени, немецким физиком Л. Прандтлем был введен множительный поправочный коэффициент, с помощью которого можно было пересчитать давление и подъемную силу профиля с учетом соответствующих данных по обтеканию его несжимаемым газом. Однако эксперименты показали, что при скоростях потока, превышающих критическую, теория Прандтля оказалась неверна.
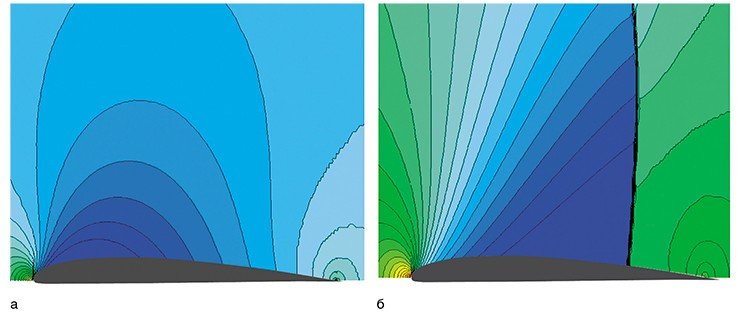
Обтекание крыла воздухом и распределение давления в потоке в докритическом режиме существенно отличается от режима, устанавливающегося при скоростях свыше критической. В качестве примера можно привести графики, на которых демонстрируются типичные примеры докритического и сверхкритического обтеканий. Скачки уплотнения возникают всякий раз, когда частицы сверхзвукового потока газа сталкиваются с поверхностью тел или меняют направление движения на конечный угол на очень малых расстояниях, сравнимых с длиной свободного пробега молекул газа.

На рисунках самолетов, проходящих сверхзвуковой барьер, хорошо видны замыкающие скачки уплотнения, возникающие при полете на сверхкритической скорости, которые зависят от формы крыльев. Когда молекула воздуха попадает в узкий слой, в котором происходит скачок уплотнения, то в результате неупругого взаимодействия молекул друг с другом часть кинетической энергии переходит в тепловую. Так как после прохождения скачка уплотнения кинетическая энергия газа уменьшается, то уменьшается и его полное давление. В термодинамике такой процесс называется необратимым. В качестве меры необратимости используется энтропия S.
В скачке уплотнения энтропия газа увеличивается. Приращение энтропии равно отношению количества кинетической энергии, перешедшей в результате неупругого взаимодействия частиц в тепловую энергию, к абсолютной температуре газа. А поскольку полная энергия газа сохраняется, и, следовательно, полная температура T0=const, то полные давления за скачком p02 и перед скачком p01 связаны соотношением:
p02= p01 • exp(-DS/R); где DS — приращение энтропии в скачке уплотнения, R — газовая постоянная.
Таким образом, полное давление газа при прохождении скачка уплотнения уменьшается. Это обстоятельство использовалось в дальнейшем для объяснения причины увеличения сопротивления профилей при их обтекании трансзвуковой скоростью набегающего потока. Скачки уплотнения ответственны также и за явление «звукового удара», которое наблюдается при полете сверхзвуковых самолетов.
ЦАГИ и решение проблемы
В 1940 г. в Центральном аэрогидродинамическом институте (ЦАГИ) им. проф. Н. Е. Жуковского — крупнейшем государственном научном авиационном центре России — под руководством академика С. А. Христиановича было вычислено сопротивление, вызванное наличием скачков уплотнения при переходе обтекающего потока из сверхзвукового режима в дозвуковой: оно получило название волнового сопротивления.
Оказалось, что скачок уплотнения приводит к падению давления в хвостовой части профиля, что вызывает рост сопротивления обтекаемого тела. Для того чтобы подтвердить теорию, нужно было провести эксперименты; с этой целью требовалось создать аэродинамическую трубу с трансзвуковой скоростью в рабочей части.
При работе над трубой ученые наткнулись на существенное физическое ограничение: оказалось, что при обтекании модели крыла трансзвуковым потоком возникающие ударные волны, отражаясь от стенок рабочей части, падают на поверхность модели и существенно меняют структуру течения. Чтобы обойти эту проблему, Христианович разработал теорию «коротких» волн, позволяющую решать задачи взаимодействия ударных волн с различными поверхностями. Оказалось, что полупроницаемые поверхности значительно ослабляют интенсивность отраженных волн — так появилась идея перфорировать стенки рабочей части трансзвуковой аэродинамической трубы.
И подобная труба впервые в мире была создана в самом ЦАГИ в 1946 г. Сейчас трубы с перфорацией стенок стали неотъемлемой частью аэродинамических лабораторий всего мира. Данная конструкция позволила получать аэродинамические характеристики моделей крыльев и фюзеляжей в трансзвуковом диапазоне чисел Маха* набегающего потока, обеспечивая непрерывный переход через скорость звука.
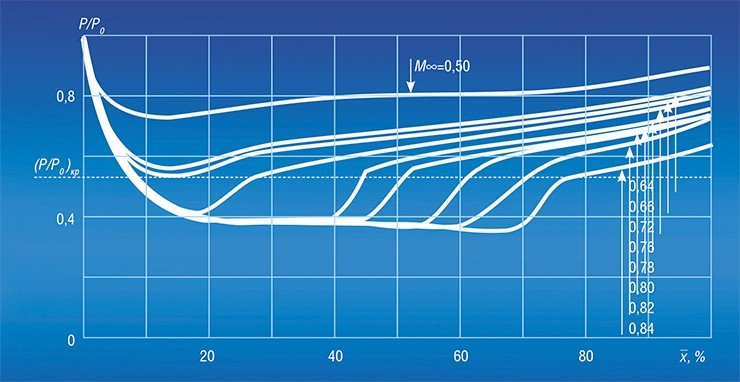
В дальнейшем задача влияния сжимаемости течения на распределение давления по крылу в короткие сроки была полностью решена Христиановичем и его сотрудниками. Был установлен фундаментальный закон стабилизации: при наступлении критической скорости сначала происходит замедление роста скорости у поверхности профиля по сравнению с ростом скорости набегающего потока. Затем возрастание скорости вообще прекращается, и распределение значений числа Маха по поверхности профиля от его носка до скачка уплотнения остается постоянным, не зависящим от скорости набегающего потока. Это распределение называется предельным распределением чисел Маха, с его помощью вычисляется «предельная кривая давления».
Иллюстрацией этого закона является распределение вдоль поверхности профиля величины отношения давления потока в точке на профиле к давлению потока в точке торможения p/p0. Это отношение связано с числом Маха выражением:
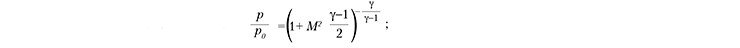
где γ — отношение теплоемкостей газа при постоянном давлении и объеме.
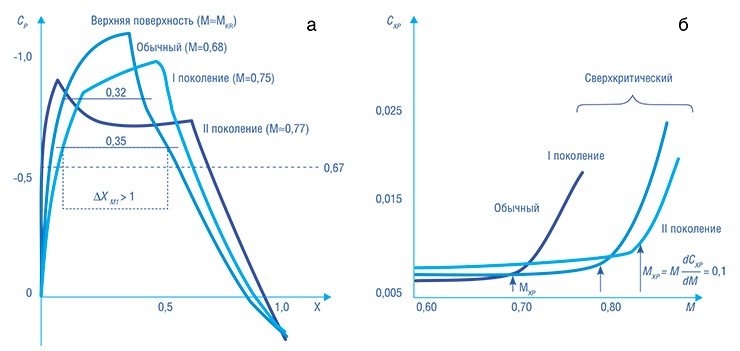
И если число Маха у поверхности остается неизменным, то и давление сохраняет постоянное значение, что, собственно, и показано на графике распределения давлений по верхней поверхности профиля.
Полученные результаты позволили Христиановичу разработать метод расчета аэродинамических характеристик трансзвуковых профилей, опирающийся на их характеристики в несжимаемом потоке. Используя этот метод, можно было вычислить предельную кривую давления, по которой, в свою очередь, вычислялись аэродинамические характеристики при числе Маха, равном единице, с последующим пересчетом на другие околозвуковые числа Маха. (Стоит отметить, что тогда еще не было ЭВМ и все расчеты производились на логарифмических линейках и арифмометрах.)
Из закона стабилизации следует, что в области сверхзвуковых скоростей и у носка профиля увеличение разрежения прекращается и падает с дальнейшим ростом числа Маха набегающего потока, или M∞. Увеличение разрежения на верхней поверхности профиля происходит лишь по причине расширения области сверхзвуковых скоростей при смещении скачка уплотнения к хвосту профиля. В то же время на нижней поверхности профиля, где скорости еще дозвуковые, разрежения продолжают интенсивно увеличиваться по мере повышения M∞.
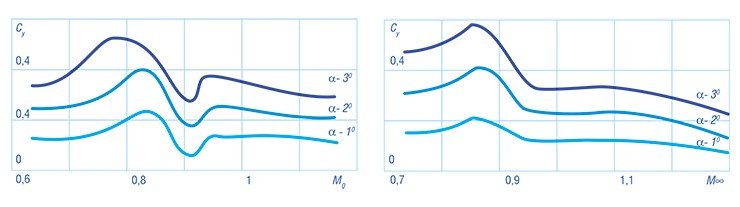
Это приводит к замедлению роста, а затем и к падению значений подъемной силы и момента крыла, как можно видеть на графике зависимости коэффициента подъемной силы от числа Маха набегающего потока. Сопротивление же, напротив, начинает возрастать из-за уменьшения разрежения в передней части профиля и появления зоны разрежения в хвостовой части профиля.
Понимание физической природы подобных режимов течения позволили предпринять практические шаги по проектированию крыловых профилей и самих крыльев, у которых эти неблагоприятные эффекты были минимизированы. Одним из шагов в этом направлении стало использование профилей с меньшей относительной толщиной, а также стреловидных крыльев, вдоль которых происходит обтекание. Сечения участков этих крыльев имеют меньшую толщину, нежели сечения, расположенные перпендикулярно их передней кромке.
 С точки зрения математики, это выглядит следующим образом: если разложить скорость набегающего потока на составляющие, одна из которых параллельна передней кромке крыла, а другая перпендикулярна к ней, то составляющая, параллельная размаху крыла, не окажет влияния на распределение давления по крылу. Обтекание крыла будет происходить так, словно на него набегает поток со скоростью, меньшей скорости набегающего потока, что благоприятствует влиянию сжимаемости на его аэродинамические характеристики. Полную теорию обтекания стреловидных крыльев разработал академик В. В. Струминский.
С точки зрения математики, это выглядит следующим образом: если разложить скорость набегающего потока на составляющие, одна из которых параллельна передней кромке крыла, а другая перпендикулярна к ней, то составляющая, параллельная размаху крыла, не окажет влияния на распределение давления по крылу. Обтекание крыла будет происходить так, словно на него набегает поток со скоростью, меньшей скорости набегающего потока, что благоприятствует влиянию сжимаемости на его аэродинамические характеристики. Полную теорию обтекания стреловидных крыльев разработал академик В. В. Струминский.
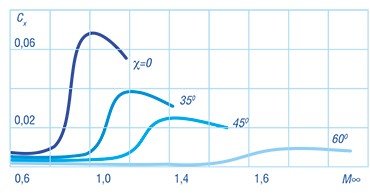
Экспериментальное подтверждение этой теории представлено на графике зависимости коэффициента сопротивления скользящих крыльев от чисел Маха для различных углов стреловидности.
К освоению «трансзвука»
В последующие годы появилась возможность моделировать на ЭВМ воздушные течения путем численного решения уравнений газовой динамики и пограничного слоя. Это позволило в ЦАГИ разработать так называемые сверхкритические крыловые профили, использование которых дало возможность увеличить скорость полета при заданной толщине и заданном значении подъемной силы. Основой для создания подобных профилей явилось понижение возмущений, вносимых в поток верхней поверхностью профиля, что привело к росту Mк. Однако при малой искривленности верхней поверхности сверхкритического профиля уменьшается доля создаваемой ею подъемной силы. Для компенсации этого явления производится «подрезка» хвостового участка нижней поверхности, что является характерной особенностью данного класса крыловых профилей.

Именно за счет повышения давления в хвостовом участке нижней поверхности профиля происходит компенсация подъемной силы, которая теряется на средней части верхней поверхности («эффект закрылка»). Низкий уровень скоростей на верхней поверхности сверхкритических профилей приводит при околозвуковом обтекании к образованию местной сверхзвуковой зоны с меньшим ускорением потока, а также смещением замыкающего скачка уплотнения в заднем направлении.
Все это уменьшает интенсивность скачка уплотнения (перепада давлений на нем) и снижает волновое сопротивление. В итоге на сверхкритическом профиле можно реализовать дальнейшее продвижение по скорости полета, т. е. увеличить значение Mк при заданной максимальной относительной толщине профиля. Важной эксплуатационной характеристикой сверхкритических профилей второго поколения является их независимость от величины подъемной силы.
На графиках распределения коэффициента давления по верхней поверхности различных профилей и зависимости коэффициента их волнового сопротивления от числа Маха показана эволюция распределения коэффициента давления и коэффициента волнового сопротивления при переходе от обычных профилей крыла к сверхкритическим. Другим направлением использования сверхкритических профилей, получившим широкое распространение в практике современного и перспективного самолетостроения, является возможность повышения относительной толщины профиля крыла при сохранении величины.
Современные скоростные профили позволяют повысить величину Mк на 0,05—0,12 или максимальную относительную толщину на 2—5 % от хорды профиля. Топливо, используемое во время полета, заливается в баки, расположенные в крыльях, поэтому толщина крыльев является очень важным конструктивным параметром. Использование сверхкритических профилей в компоновке стреловидных крыльев на сегодняшний день можно назвать одним из основных направлений совершенствования аэродинамики пассажирских и транспортных самолетов.
В ЦАГИ и ИТПМ им. С. А. Христиановича СО РАН были спроектированы серии крыловых профилей, характеризующихся максимальным критическим числом Маха полета. Характерной особенностью таких профилей является достаточно протяженный участок верхней поверхности профиля, вдоль которого поток движется со скоростью звука, т. е. с M=1 . Это позволяет сместить замыкающий скачок уплотнения на заднюю кромку крыла, в результате чего волновое сопротивление максимально понижается.
Следует отметить, что задачи аэродинамического проектирования требуют комплексного подхода. Так, задачи обтекания должны решаться точно и быстро, при том что проблема оптимизации требует многократного решения этих задач для различных конфигураций. Методы оптимизации должны позволять получать решение с учетом аэродинамических и геометрических ограничений за вполне обозримое время. Эти особенности потребовали разработки новых методов.
На основе вышеперечисленных требований были разработаны методы для решения уравнений течений газа, генерации вычислительной сетки, представления геометрии варьируемой границы и метод оптимизации. В ИТПМ им. С. А. Христиановича СО РАН на их основе был создан пакет прикладных программ для проектирования оптимальных крыловых профилей, удовлетворяющих заданным аэродинамическим и геометрическим ограничениям. Впервые благодаря решению прямой проблемы оптимизации, которую удалось свести к задаче нелинейного программирования при произвольных начальных условиях, были получены конфигурации дозвуковых профилей, обтекаемых с максимальным критическим числом Маха.
С помощью данных программ исследователи смогли достичь конкретных результатов в проектировании профилей со значительной относительной толщиной (18 % и выше), которые характеризуются отмеченными выше физическими особенностями обтекания. Для используемых сейчас профилей с относительной толщиной 9—12 % удалось достигнуть крейсерских скоростей полета 900—950 км/час.
На «горячих» крыльях
В настоящее время с целью управления потоком используются новые принципы и современные технические средства, например подвод энергии в поток. Так, согласно теоретическим разработкам, ведущимся в ИТПМ, управляя обтеканием обычных, не сверхкритических, профилей с помощью импульсно периодического подвода энергии, можно вдвое снизить волновое сопротивление, что позволит продвинуться в область более высоких скоростей полета.
Подобный подвод энергии может быть осуществлен при помощи комбинации лазерного и СВЧ-излучения. Лазерное излучение при этом инициирует незначительную, но достаточную для эффективного поглощения СВЧ-излучения, ионизацию потока.
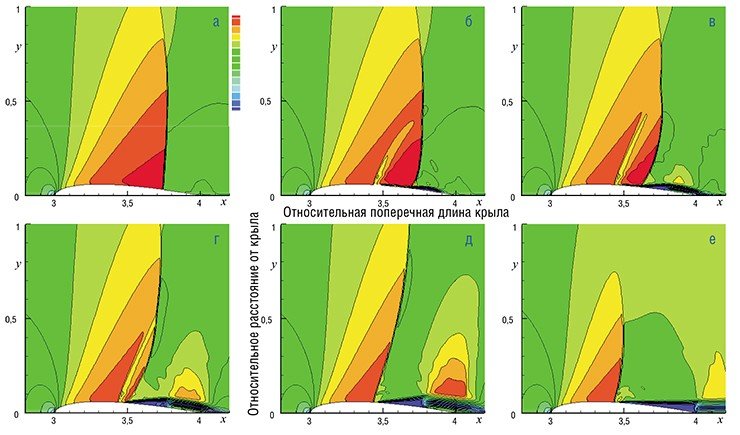
Для выяснения причин столь существенного снижения сопротивления необходимо рассмотреть как динамику процесса, так и установившийся периодический режим течения воздушного потока. На серии графиков, демонстрирующих изменение размеров сверхзвуковой зоны и интенсивности замыкающего скачка при подводе энергии, показано поле чисел Маха при обтекании симметричного профиля.
На конечном графике видно, что результирующий замыкающий скачок уплотнения стабилизируется перед зоной подвода энергии с незначительными продольными колебаниями, обусловленными периодическим подводом энергии. Интенсивность замыкающего скачка оказывается меньше интенсивности скачка в случае, когда энергия не подводится, поскольку он формируется при меньших числах Маха. Этим обусловлено и то, что газ, проходя через скачок уплотнения, теряет меньше кинетической энергии. Тем самым обеспечивается большее значение полного давления в хвостовой части профиля, что позволяет снизить лобовое сопротивление.
Подвод энергии способствует не только описанной перестройке течения, но и не зависящему от нее повышению полного давления газа p01 , за счет мгновенного повышения температуры в объеме. Оценки показывают, что требуемая мощность подводимой энергии мала по сравнению с мощностью набегающего потока. Это обстоятельство представляется чрезвычайно важным, так как гарантирует высокую эффективность подобного способа управления обтеканием профиля.
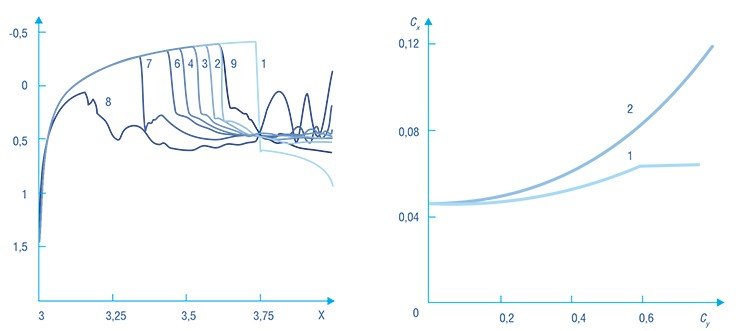
Физический механизм уменьшения волнового сопротивления профиля при подводе энергии отличается от механизма сверхкритических профилей. Для сверхкритических профилей уменьшение волнового сопротивления достигается с помощью смещения замыкающего скачка уплотнения в хвостовую часть. Судя по графику распределения коэффициента давления вдоль хорды профиля, без подвода и с подводом энергии, в различных зонах профиля, существенно большие значения давления реализуются на большей части профиля, начиная с передней точки зоны подвода энергии.
Для оценки аэродинамических качеств исследуемого объекта обычно используется график зависимости коэффициента лобового сопротивления профиля Cx (иначе — аэродинамическая поляра) от коэффициента подъемной силы Cy. Аэродинамическая поляра профиля с несимметричным подводом энергии только у нижней поверхности также кардинально отличается от поляры без подвода энергии, получаемой при обтекании под различными углами атаки. При таком подводе энергии требуемая подъемная сила может быть достигнута благодаря меньшему волновому сопротивлению, что увеличивает аэродинамическое качество профиля.
Интересно, что при монотонном увеличении подводимой энергии коэффициент сопротивления стабилизируется. Точка, соответствующая началу стабилизированного участка, обозначает оптимальный режим полета исходя из условия максимума дальности, а также с учетом увеличения аэродинамического качества и снижения затрат топлива на нагрев газа.
В этой точке коэффициент подъемной силы меньше соответствующего значения при максимальном аэродинамическом качестве без подвода энергии. Поэтому крейсерский полет при подводе энергии должен осуществляться на меньших высотах, чем полет без подвода энергии, — это следует из условия равенства аэродинамической подъемной силы весу самолета.
Факт стабилизации коэффициента сопротивления позволяет также управлять значением подъемной силы при постоянном значении силы волнового сопротивления. Подвод энергии к газу при обтекании сверхкритических профилей целесообразно осуществлять только на нижней поверхности, так как на верхней поверхности замыкающий скачок уплотнения смещен к задней кромке крыла. Используя описанный подход, можно увеличить дальность полета до 15 %!

Проблемы, связанные с преодолением сверхзвукового барьера для мирных целей, не теряют своей остроты. Летать быстрее и дальше, а следовательно, тратить на перелеты меньше времени и денег — вот актуальная задача современной цивилизации.
И хотя пока не освоены даже трансзвуковые скорости, прогресс в этом направлении очевиден, и мы вправе в ближайшем будущем ожидать появления новых подходов к решению проблем, сформулированных еще академиком Христиановичем. Пассажирская авиация стоит сейчас перед звуковым барьером — и этот барьер, как и многие другие в «технологической» истории нашей цивилизации, будет обязательно взят!
* Безразмерная характеристика скорости, называемая числом Маха, равна отношению скорости полета к скорости распространения звуковых волн. Число Маха, соответствующее критической скорости полета, называется критическим числом Маха µk













