Соболев из школы Эйлера
К 100-летию со дня рождения Сергея Львовича Соболева – представителя российской математической школы, вошедшего в список ученых, чье творчество создало главные интеллектуальные сокровища мировой культуры
Математика изучает формы мышления. В самом общем смысле дифференцирование – определение тенденций процесса, а интегрирование – предсказание будущего по тенденциям.
Современное человечество не мыслит себя без интегрирования и дифференцирования. Дифференциальное и интегральное исчисление открыто Ньютоном и Лейбницем. Используя понятия, предложенные Ньютоном и Лейбницем, Эйлер взрастил и выпестовал новую математику переменных величин, совершив немало гениальных открытий и создав неисчерпаемую собственную коллекцию поразительных формул и теорем.
Двести лет математический анализ оставался исчислением Ньютона, Лейбница и Эйлера. В двадцатом веке классическое исчисление превратилось в теорию распределений. Ключевыми объектами современного анализа стали интеграл в смысле Лебега и производная в смысле С. Л. Соболева, определенные для самых общих зависимостей, не подвластных операциям классического дифференцирования и интегрирования. Лебег и Соболев вошли в историю, предложив новые подходы к интегралу и производной, существенно расширив сферы влияния и области приложений математики.
Исторические фигуры и открытия достойны исторических параллелей и анализа. Математический дар передается от учителя к ученику. Эта чередующаяся цепь преемственных поколений – материальный носитель математической школы. Соболев принадлежит к школе, ведущей родословную от Леонарда Эйлера.
От Эйлера до Соболева
Человек – объект физический и может быть отчасти представлен своей мировой линией в четырехмерном пространстве-времени. Большая часть мировой линии Эйлера принадлежит России. Уроженец Швейцарии, Эйлер нашел в России свою вторую Родину и покоится в Петербурге. «Да Винчи» от математики, он давно стал неотъемлемой частью русского духа.
Нет ни швейцарской, ни русской математики, но есть математика в России, есть отечественная математиче-ская традиция и отечественная математическая школа. Наши соотечественники с гордостью считают Эйлера основателем российской математической школы.

Усилиями Эйлера Петербург стал математической столицей мира XVIII в. Даниэл Бернулли писал Эйлеру: «Я не могу Вам довольно выразить, с какою жадностью повсюду спрашивают о Петербургских мемуарах». Речь идет о знаменитых «Комментариях Санкт-Петербургской Академии», ставших ведущим научным журналом той эпохи. Это издание не раз меняло свое название и превратилось со временем в Известия РАН (серия математическая). Журнал Петербургской Академии наук поместил 473 статьи Эйлера, которые поочередно выходили в свет в течение многих лет после кончины Эйлера вплоть до 1830 г.
В начале XIX в. центр математической мысли переместился во Францию, где творили Лаплас, Пуассон, Фурье и Коши. Идеи новых творцов математики воспринял М. В. Остроградский, учившийся в Париже после лишения законно полученного аттестата об окончании Харьковского Императорского университета. Репутация, приобретенная Остроградским во Франции, и ряд мемуаров, представленных Академии наук, способствовали признанию его заслуг в России. Он быстро стал признанным лидером российской математики.
Остроградский прекрасно понимал значение Эйлера для отечественной науки. Именно он энергично ставил вопрос об издании наследия Эйлера. В пояснительной записке по этому поводу М. В. Остроградский писал: «Эйлер создал современный анализ, обогатив его один сам более, чем все его предшественники вместе, и сделал из него самый могущественный инструмент ума человеческого». Издание в 28 томах предполагалось осуществить в течение 10 лет, но средств у Академии наук на это не нашлось ни в то время, ни по сей день…
Многие известные математики и механики России испытали на себе влияние М. В. Остроградского. В том числе к петербургской ветви школы Остроградского относились П. Л. Чебышев, А. М. Ляпунов и В. А. Стеклов. Среди учеников Чебышева были А. Н. Коркин и А. А. Марков, у которых учился Н. М. Гюнтер, ставший научным руководителем дипломной работы С. Л. Соболева. Вторым своим учителем Соболев считал В. И. Смирнова – ученика В. А. Стеклова, ученика А. М. Ляпунова. Такова блестящая цепь научного генеалогического древа С. Л. Соболева.
Математика России в 1930-е
Великие открытия – вехи неизбежности, которые не возникают сами собой. Необходимость прокладывает свой путь через дремучую чащу случайностей. Открытия, сделанные Соболевым, относятся к годам великого перелома в мировой и отечественной математике.

Двадцатый век по праву считается веком свободы. Свобода – понятие историческое, отражающее способ разрешения конфликта между безграничными в своем разнообразии индивидуальностями и ограничивающими формами их коллективного сосуществования. Исторический антураж – обязательный компонент каждого триумфа и каждой трагедии.
Развитие социальных институтов демократии проходило одновременно с раскрепощением всех сторон духовной жизни людей. Математика раскрывала свою сущность науки о свободных формах мышления.
Идея пересмотра понятия решения дифференциального уравнения носилась в математической атмосфере начала XX в. Осмысливая свои достижения в 1957 г., сам Соболев отмечал: «В процессе изучения разнообразных задач на отыскание функций, удовлетворяющих некоторым уравнениям в частных производных, оказалось полезным использовать класс функций, не обладающих повсюду непрерывными производными нужного порядка, но являющихся в некотором смысле предельными для настоящих решений уравнений. Такие обобщенные решения ищутся, естественно, в различных функциональных пространствах, иногда полных, а иногда специально пополняемых при помощи введения новых«идеальных элементов».
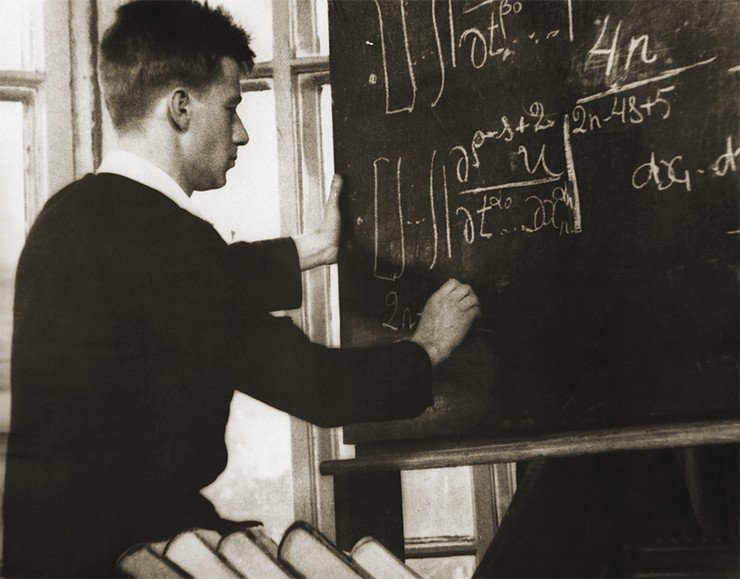
Мы никогда не боялись сдавать ему экзамен. Он опрашивал достаточно быстро: убеждался, что студент знает предмет, и сразу ставил оценку.
В те времена мы уже знали, что Соболев – знаменитый математик, но даже и не подозревали, какую ответственность он нес на другой работе, в Институте атомной энергии».
и ИВМ РАН В. И. Лебедев)
От индивидуального решения наука перешла к изучению функциональных пространств, операторов в них и тех элементов, которые являются решениями.
Вопрос о том, когда эти обобщенные решения будут решениями в классическом смысле, при таком рассмотрении становится самостоятельным.
Как мы видим, Соболев выделил неразрывную связь своей теории с гильбертовой идеей социализации математических проблем, опиравшуюся на теорию множеств Кантора.
Нет сомнений, что обращение Соболева к этой проблематике связано с Гюнтером, который пропагандировал идеи Лебега о необходимости пересмотра подхода к уравнениям математической физики на основе теории функций множеств.
 С идеями функционального анализа Соболев знакомился в семинаре, организованном Смирновым. Именно в этом семинаре изучалась классическая книга Дж. фон Неймана по математическим методам квантовой механики. Идеи Неймана вызвали интерес и у другого участника семинара Смирнова – Л. В. Канторовича, университетского товарища Соболева, который опубликовал в 1935 г. две заметки в ДАН СССР, посвященные проблеме расширения понятия функции в духе К. Фридрихса и содержащие описание обобщенного дифференцирования умеренных периодических распределений.
С идеями функционального анализа Соболев знакомился в семинаре, организованном Смирновым. Именно в этом семинаре изучалась классическая книга Дж. фон Неймана по математическим методам квантовой механики. Идеи Неймана вызвали интерес и у другого участника семинара Смирнова – Л. В. Канторовича, университетского товарища Соболева, который опубликовал в 1935 г. две заметки в ДАН СССР, посвященные проблеме расширения понятия функции в духе К. Фридрихса и содержащие описание обобщенного дифференцирования умеренных периодических распределений.
Представляется совершенно невероятным, чтобы Соболев и Канторович, близкие друзья и участники одного семинара, не знали о работах друг друга на родственные темы. Однако ни тот, ни другой никогда не упоминали об этом эпизоде в дальнейшем. Очевидном, что в те годы между Соболевым и Канторовичем, поддерживавшими теплую и сердечную дружбу до конца своих дней, имело место временное взаимное отчуждение. Понять его природу помогают исключительно острые политические события, развернувшиеся в то время в математической среде Ленинграда и Москвы.
Обстановка в математическом сообществе страны мало отличалась от общих нравов той эпохи. Против старой профессуры Северной столицы был развернут «ленинградский математический фронт». Главным объектом атаки стал возглавлявший Петроградское математическое общество Гюнтер, который был по полной программе обвинен в идеализме и отрыве от практики и получил клеймо «реакционера в общественной жизни» и «консерватора в науке». Среди подписавшихся под «Декларацией инициативной группы по реорганизации Ленинградского физико-математического общества» от 10 марта 1931 г., содержащей ужасные обвинения против Гюнтера, указан и Канторович. Гюнтер оставил руководство кафедрой и был вынужден написать покаянное письмо, впрочем, также заклейменное «математиками-материалистами». К среде идеалистов был причислен также Стеклов. К чести Соболева и Смирнова, они не присоединились к публичной травле своих наставников. Антидотом послужила явная близость научных взглядов учителей и учеников.
Старую профессуру травили и в Москве. К участию в дрязгах москвичи пытались привлечь и Канторовича, но он от каких-либо нападений на Лузина воздержался, в то время как Соболев, к сожалению, принял активное участие в работе академической комиссии по «делу Лузина».
Трагедия математики в России была всеобщей. Всеобщими были и ее триумфы.
Соболев и бомба
Сила человека – в способности создавать и передавать идеальные неосязаемые ценности. Математика хранит древнейшие технологии безошибочных интеллектуальных приемов. Наука и искусство доказательных исчислений, математика расположена в эпицентре культуры. Свобода мышления – это sine qua non личной свободы человека. Математика, положенная в основу мировоззрения, становится основой и гарантом его свободы. Творчество Эйлера и лучших представителей его школы дают тому неисчислимые примеры. Не стала исключением и судьба Соболева.

В XX в. человечество подошло к краю безопасных границ своего существования, проявив неспособность остановить поджигателей Первой и Второй мировых войн. Гарантом свободы стало оружие сдерживания. Создание атомной бомбы в США и России – демонстрация удивительной силы науки – последнего резерва выживания человечества. Математики могут гордится участием своих коллег в этом процессе. В Манхеттенском проекте работали Нейман и Улам. В осуществлении отечественного проекта «Энормоз» участвовали Соболев и Канторович.
Если же нам случалось расшуметься, Сергей Львович никогда не ругался. Это брала на себя мама, и очень быстро нас усмиряла.
Отец очень любил общаться с детьми. Нас было у него семеро, и он часто мечтал, что когда мы вырастем, то станем жить в разных городах. Тогда бы он мог на старости лет ездить в гости от одного к другому. К сожалению, эта мечта не сбылась. Он уже плохо себя чувствовал, когда вернулся из Сибири в Москву, и больше никуда не выезжал.
Сергей Львович был очень мягким человеком. Если мне что-то не нравилось из того, что он говорил, я могла сказать: “Ой, что за глупость”, и он не только не обижался (а в те времена такой тон многих бы возмутил), но доказывал, что я не права. Он был вполне демократичен, и единственное, что нам не разрешалось, это обижать маму. Здесь он был непреклонен.
Кроме того, он страшно не любил склок. Нам, детям, не всегда удавалось жить мирно, но он не разбирался. Если двое дерутся – значит, и виноваты двое! Это была его твердая установка в тех редких случаях, когда ему приходилось нас разнимать.
Он очень не любил, когда люди говорят неправду. Часто ложь строится из полуправды и выглядит красиво. Он это ненавидел…
Сергей Львович часто писал стихи. Когда в детстве нам приходилось жить в разных городах, он всегда присылал нам письма с собственными стихами. Стихи были разные, обо всем на свете. К сожалению, все они утеряны».
В настоящее время большинство документов, касающихся истории создания ядерного оружия, рассекречено и опубликовано, и мы можем ощутить накал той героической эпохи.
Начало работ по атомному проекту в нашей стране принято связывать с распоряжением ГКО № 2352сс «Об организации работ по урану» от 28 сентября 1942 г. Спустя несколько месяцев ГКО принимает решение об организации Лаборатории № 2 АН СССР для изучения атомной энергии. Руководство Лабораторией и всеми работами по атомной проблеме было поручено И. В. Курчатову. Вскоре одним из заместителей Курчатова был назначен Соболев, который вошел в группу И. К. Кикоина, где занимались проблемой обогащения урана с помощью каскадов диффузионных машин для разделения изотопов.

Соболев был блестящим популяризатором и выступал перед различными аудиториями. Ему случалось разъяснять школьникам, что такое функциональный анализ. И хотя до самых сложных вещей речь не доходила, но о месте и значении этой области математики ему удавалось рассказать удивительно грамотно и доходчиво!».
В особой папке хранится отчет Курчатова и Кикоина, датированный августом 1945 г. В преамбуле этого документа говорится: «Из четырех известных за границей способов получения атомных взрывчатых веществ (урана-235 и плутония-239), а именно: способом «котел уран – графит», способом «котел уран – тяжелая вода», способом диффузионным, способом магнитным, руководящие работники Лаборатории № 2 (академики Курчатов, Соболев, члены-корреспонденты Академии наук Кикоин, Вознесенский) считают, что по трем первым из указанных способов Лаборатория № 2 в настоящее время имеет уже достаточные данные для проектирования и сооружения установок».
 Уже в 1946 г. построены первые газовые компрессоры и освоено их серийное производство. Начались эксперименты по обогащению газообразного шестифтористого урана. Работа требовала решения колоссального числа разнообразных научных, технологических и организационных проблем, ставших на долгие годы главным делом Соболева. Соболев работал как в группе по плутонию-239, так и в группе по урану-235, организовывал и направлял работу вычислителей, разрабатывал вопросы регулирования процесса промышленного разделения изотопов, отвечал за снижение потерь и решал массу иных организационных и технических вопросов. Его роль в атомном проекте возрастала.
Уже в 1946 г. построены первые газовые компрессоры и освоено их серийное производство. Начались эксперименты по обогащению газообразного шестифтористого урана. Работа требовала решения колоссального числа разнообразных научных, технологических и организационных проблем, ставших на долгие годы главным делом Соболева. Соболев работал как в группе по плутонию-239, так и в группе по урану-235, организовывал и направлял работу вычислителей, разрабатывал вопросы регулирования процесса промышленного разделения изотопов, отвечал за снижение потерь и решал массу иных организационных и технических вопросов. Его роль в атомном проекте возрастала.
Испытание РДС-1 состоялось около Семипалатинска 29 августа 1949 г. Ровно через два месяца более восьмисот участников атомного проекта наградили орденами. Соболев получил орден Ленина.
Еще в середине 1949 г. Лаборатория № 2 была переименована в ЛИПАН – Лабораторию измерительных приборов Академии наук. В ЛИПАНе Соболев и написал главную книгу своей жизни – «Некоторые применения функционального анализа в математической физике».
Атомный проект обогатил научный и личностный потенциал Соболева. До конца жизни огромное место в его творчестве заняла вычислительная математика. В 1952—1960 гг. он возглавлял кафедру вычислительной математики МГУ. Уже в Сибири Соболев построил теорию кубатурных формул, удивительную красотой своей универсальности. В ней Соболев синтезировал идеи классических приближенных методов и теории распределений.
Работа в ЛИПАНе добавила Соболеву новые яркие краски в понимании математики. По его словам, именно в те годы он понял, что для многих задач важен не абстрактный вопрос существования решения, а конкретное предъявление разумного приближенного варианта к назначенному сроку.
Новая производная – новое исчисление
Эйлер еще в 1755 г. дал универсальное определение функции, которое почти двести лет воспринималось как наиболее общее и совершенное. В своем знаменитом курсе дифференциального исчисления он писал: «Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменениям, то первые называются функциями вторых. Это наименование имеет чрезвычайно широкий характер; оно охватывает все способы, какими одно количество может определяться с помощью других. Итак, если x обозначает переменное количество, то все количества, которые как-либо зависят от x, т. е. определяются им, называются его функциями».

Исследования Соболева связаны с переосмыcлением понятия решения дифференциального уравнения. Соболев предложил решать задачу Коши в пространстве функционалов, то есть отказаться от стандартного понимания решения как функции. Фактически Соболев стал считать дифференциальное уравнение решенным даже в тех случаях, когда нам доступны всевозможные интегральные характеристики поведения процесса. При этом решение как функция времени может быть не только неизвестным, но и просто отсутствующим. В науку вошло качественно новое понимание ключевых принципов прогнозирования.
В то время фактически еще не существовало электронных машин, и вместо процессоров для вычислений использовались… молодые женщины, потому что они делают меньше ошибок, чем мужчины.
И вот представьте себе помещение, где много-много столов, за которыми сидят девушки. Каждой дано задание за день сделать определенное количество вычислений. Это очень тяжелая работа, причем девушки даже не знали, для чего будут использованы результаты.
Соболев был “маршалом”: именно он разбивал задачу на кусочки, которую его “генералы” и “полковники” дробили дальше. В итоге до низа доходили уже просто задания “посчитать вот это и это”.
Вот таким способом он использовался на этой работе. Когда его спрашивали: “Почему именно Вы?”, он отвечал: “Могли бы и другие, но, видимо, я делал это лучше”».
М. Д. Рамазанов)
Обобщенные производные Соболева под эйлерово понятие функции не подпадают. Дифференцирование, предложенное Соболевым, опирается на новое понимание взаимозависимости математических величин. Обобщенная функция определяется неявно с помощью интегральных характеристик своих воздействий на всех представителей заранее выбранного класса пробных функций.
Соболев был среди пионеров применения функционального анализа в математической физике, создав свою теорию в 1935 г. В работах Лорана Шварца, независимо пришедшего к тем же идеям спустя десятилетие, новое исчисление стало общедоступным, представ в виде элегантной, мощной и чрезвычайно прозрачной теории распределений, утилизировавшей многие прогрессивные идеи алгебры, геометрии и топологии.
Дифференциальное исчисление XVII в. неотделимо от общих воззрений классической механики. Теория обобщенных функций связана с механикой квантовой.

«Однажды я стал невольным свидетелем его телефонного разговора с одним очень уважаемым человеком. Они обсуждали какую-то острую проблему. Атмосфера накалилась, обсуждение дошло до крайней точки, и Сергей Львович положил трубку. На вопрос, сколько времени ему потре6уется, чтобы прийти в себя после такого стресса, он ответил: «Пустяки. Я сажусь за работу, и через пять минут забываю обо всем»
Следует особо подчеркнуть, что квантовая механика не является простым обобщением классической механики, а представляет научное мировоззрение, основанное на новых законах. Классические детерминизм и непрерывность уступили место квантованию и неопределенности. В XX в. человечество вышло на совершенно иной уровень понимания природных процессов.
Аналогичным образом дело обстоит и с математическими теориями современности. Логика наших дней не является обобщением логики Аристотеля. Геометрия банаховых пространств не служит обобщением евклидовой планиметрии. Теория распределений, ставшая исчислением нашего времени, коренным образом преобразила всю технологию математического описания физических процессов с помощью дифференциальных уравнений.
Открытия Ньютона и Лейбница подытожили многовековую предысторию дифференциального и интегрального исчисления, открыв дорогу новым исследованиям. Достижения Лебега и Соболева продолжили размышления их гениальных предшественников и осветили путь математиков нашего времени.
Соболев слышал будущее и одаривал людей своими пространствами. Его открытия стали триггером многих революционных изменений математики, счастливыми свидетелями и участниками прогресса которой мы являемся.

Последняя серия математических работ Соболева была посвящена тонким свойствам корней полиномов Эйлера…
Литература
Атомный проект СССР. Документы и материалы. Т. II: Атомная бомба 1945—1954 / Ред. Рябев Л. Д. М.; Саров: Наука, 2000.
Кутателадзе С. С. Сергей Соболев и Лоран Шварц // Вест. РАН. 2005. Т. 75, вып. 4. С. 354—359.
Нейман, Иоганн фон. Математические методы квантовой механики. М.: Наука, 1964.
Николай Петрович Дубинин и XX век / Сост. Дубинина Л. Г., Овчинникова И. Н. М.: Наука, 2006.
Сергей Львович Соболев. Cтраницы жизни в воспоминаниях современников / Ред. Рамазанов М. Д. Уфа: ИМВЦ УНЦ РАН, 2003.
Смирнов В. И., Соболев С. Л. Биографический очерк [Николай Максимович Гюнтер (1871—1941)] // Гюнтер Н. М.Теория потенциала и ее применение к основным задачам математической физики. М.: ГИТТЛ, 1953. С. 393—405.
Соболев С. Л. Введение в теорию кубатурных формул.М.: Наука, 1974.
Соболев С. Л. Избранные труды. Т. 2. Новосибирск: Ин-т математики СО РАН, 2006.
Философские проблемы современного естествознания / Ред. Федовеев Н. П. и др. М.: Изд-во АН СССР, 1959.
Эйлер Л. Дифференциальное исчисление. Л.: Гостехиздат, 1949.
Lutzen J. The Prehistory of the Theory of Distributions. New York etc.: Springer, 1982.
Schwartz L. A Mathematician Grappling with His Century. Basel etc.: Birkhauser, 2001.
Редакция и автор благодарят Е. С. Соболеву, пресс-секретаря Президиума СО РАН О. В. Подойницыну, сотрудников библиотеки ИМ СО РАН, директора издательства Т. Н. Рожковскую за помощь в подготовке публикации.
В статье использованы материалы из архивов семьи С. Л. Соболева, Института математики им. С. Л. Соболева СО РАН, Президиума СО РАН