Сверхизолятор: сверхпроводник наоборот
Совместные работы сотрудников Института физики полупроводников СО РАН (Новосибирск) с исследователями из Аргонской национальной лаборатории (США), Университета Регенсбурга (Германия) и Межуниверситетского центра по микроэлектронике (Бельгия) привели к открытию сверхизолирующего состояния вещества, являющегося полным антиподом сверхпроводящего состояния и возникающего благодаря сверхпроводимости. Сообщение об этом открытии было опубликовано в журнале Nature в апреле 2008 г. Известно, что область существования сверхпроводимости ограничена максимальными значениями плотности тока, температуры и магнитного поля. Многочисленные эксперименты показали, что в тонких пленках критическая температура, как правило, значительно меньше, чем в объемном материале, а достаточно тонкие пленки могут вообще оказаться несверхпроводящими. Таким образом, в дополнение к критическим значениям плотности тока, температуры и магнитного поля существует еще и критическая толщина пленки – при уменьшении толщины ниже критической пленка может стать не только металлом, но и изолятором. Исследование двумерной сверхпроводимости и этого необычного перехода сверхпроводник-изолятор, происходящего в пленках толщиной несколько нанометров, стало одной из ключевых проблем в физике конденсированного состояния за последние 20 лет. Занимаясь изучением сверхпроводящих свойств тонких пленок нитрида титана, авторы открытия обнаружили, что при низких температурах пленки претерпевают очень резкий переход сверхпроводник-изолятор без промежуточной металлической фазы. Дальнейшие исследования этого явление привели ученых к пониманию природы процессов, которые могут создавать не только сверхпроводящее состояние, но и его полную противоположность – сверхизолирующее состояние
«Чтобы сделать экспериментальное открытие,
мало наблюдать какой-то эффект,
нужно также понимать смысл и значение этого наблюдения»
И. Гиавер
Cверхпроводимость, то есть способность некоторых веществ проводить ток без тепловых потерь, возникает вследствие взаимодействия электронов с колебаниями атомов в решетке. В результате этого опосредованного взаимодействия, электроны, которые будучи одинаково заряженными частицами должны были бы отталкиваться, начинают притягиваться и образовывать связанные пары. Эти пары электронов называют куперовскими парами. В то время как отдельные электроны являются ферми-частицами, и каждый из них требует для себя индивидуального квантового состояния, куперовские пары ведут себя как бозе-частицы. Это значит, что при достаточно низкой температуре куперовские пары соберутся или, как говорят, сконденсируются в одном наинизшем по энергии квантовом состоянии, образуя куперовский конденсат. Чтобы вырвать куперовскую пару из этого конденсата и превратить ее в два не связанных электрона, необходимо затратить некоторую энергию. Минимальное значение энергии Emin = 2∆, где ∆, называемая сверхпроводящей щелью, и есть энергия, отделяющая наинизшее квантовое состояние от состояний, которые могут заниматься отдельными, не связанными электронами. Куперовский конденсат описывается единой волновой функцией для всего объема вещества. При протекании тока весь конденсат движется как единое целое, при этом составляющие его пары остаются в наинизшем энергетическом состоянии.

Напомним, что протекание тока в обычном проводнике, обусловлено ускорением электронов электрическим полем. При этом электроны приобретают энергию и поднимаются на более высокие энергетические уровни. Этот процесс не бесконечен, и через некоторое время, называемое временем энергетической релаксации, электрон отдает излишек энергии кристаллической решетке. Такая перекачка энергии приложенного электрического поля в кристаллическую решетку и есть механизм электросопротивления и источник тепловых (джоулевых) потерь, что проявляется как нагрев проводника.
В сверхпроводнике, из-за наличия сверхпроводящей щели, куперовские пары, входящие в сверхпроводящий конденсат, могут двигаться с постоянной скоростью до тех пор, пока их кинетическая энергия не превосходит Emin = 2∆, оставаясь при этом в наинизшем энергетическом состоянии. Другими словами, электрический ток в сверхпроводнике может течь без приложения электрического поля, то есть без затрат энергии. Например, если свернуть сверхпроводящий провод в кольцо, то ток будет течь бесконечно долго, что и является иллюстрацией отсутствия сопротивления.
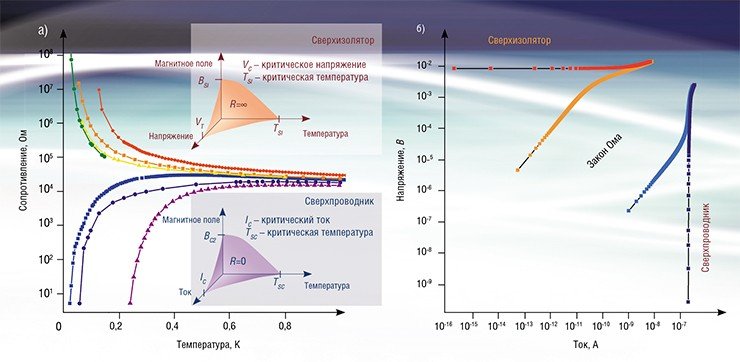
Понятно, что слишком большой ток, при котором кинетическая энергия пары электронов в конденсате становится равной 2∆, разрушает сверхпроводимость. К такому же результату приводит значительное повышение температуры или помещение вещества в сильное магнитное поле. То есть, область существования сверхпроводимости ограничена максимальными значениями плотности тока, температуры и магнитного поля, что принято изображать в виде фазовых диаграмм. Критические значения плотности тока, температуры и магнитного поля по сути являются паспортными данными конкретного материала.
Многочисленными экспериментами было показано, что в тонких пленках критическая температура, как правило, значительно меньше, чем в объемном материале, а достаточно тонкие пленки могут вообще оказаться несверхпроводящими. Таким образом, в дополнение к критическим значениям плотности тока, температуры и магнитного поля существует еще и критическая толщина пленки. При этом выяснилось, что влияние этого параметра может принципиально отличаться от привычного действия всех остальных. А именно, при уменьшении толщины ниже критической пленка может стать не только металлом (что было бы вполне ожидаемым эффектом), но и изолятором. Исследование двумерной сверхпроводимости и этого необычного перехода сверхпроводник–изолятор, происходящего в пленках толщиной несколько нанометров, стало одной из ключевых проблем в физике конденсированного состояния в последние 20 лет.
В зеркале низких температур
Занимаясь в Институте физики полупроводников СО РАН изучением сверхпроводящих свойств тонких пленок нитрида титана, изготовленных в Бельгии в Межуниверситетском центре по микроэлектронике, мы обнаружили, что они претерпевают очень резкий переход сверхпроводник–изолятор без промежуточной металлической фазы: пленки, практически не отличающиеся ни по толщине, ни по температурному поведению сопротивления при температуре выше 0,5 К, при низких температурах однозначно выбирают, быть им сверхпроводником или изолятором. Именно на этой узкой критической области перехода сверхпроводник–изолятор сосредоточились наши исследования, часть которых мы проводили в университете города Регенсбург в Германии, где были доступны более низкие температуры. Главной задачей стало выяснение природы изолирующего состояния, формирующегося в пленках, которые, казалось бы, имели все шансы быть сверхпроводящими. Довольно быстро выяснилось, что свойства этих изоляторов принципиально отличаются от свойств обычных изоляторов с запрещенной зоной в электронном спектре. Например, ширина запрещенной зоны в наших изоляторах оказалась сильно зависящей от магнитного поля: вначале, при приложении внешнего магнитного поля, она возрастает почти вдвое, затем уменьшается до нуля, и в сильном магнитном поле изолятор превращается в металл. Свойства сверхпроводников в критической области также оказались весьма необычными: приложение относительно слабого внешнего магнитного поля тут же переводило сверхпроводящие пленки в изолирующее состояние, а при усилении поля происходил переход в металлическое состояние.
Еще более интригующим оказалось поведение изоляторов при приложении напряжения. При умеренных температурах, величина тока была пропорциональна приложенному напряжению, то есть следовала закону Ома. Однако при уменьшении температуры эта зависимость внезапно становилась пороговой: до тех пор пока приложенное напряжение оставалось меньше некоторой критической величины, ток не протекал, то есть сопротивление пленки было практически бесконечно; при достижении критического напряжения ток скачком возрастал на много порядков. Удивительным образом, вольт-амперные характеристики наших изоляторов и сверхпроводников оказались зеркальными.
Весь комплекс исследований, включающий также и данные, полученные методом сканирующей электронной микроскопии при температурах вплоть до 0,05 К, привел нас к заключению, что в изоляторах, формирующихся в критической области, куперовский конденсат продолжает существовать: он присутствует в виде отдельных сверхпроводящих капель. Такой изолятор мы назвали куперовским. Таким образом, критические пленки можно рассматривать как джозефсоновскую сетку – систему сверхпроводящих островков, соединенных джозефсоновскими связями. В критической области эта система находится в равновесии, которое очень легко разрушить. Достаточно крошечного усиления джозефсоновских связей при понижении температуры и независимые островки сольются в сверхпроводящий материк – пленка станет сверхпроводящей. Если же структурные неоднородности пленки окажутся чуть большими и приведут к рассогласованию реакции связей между островками, то при понижении температуры сверхпроводящие островки станут еще более изолированными – пленка превратится в еще более сильный изолятор. Концепция джозефсоновской сетки замечательно объясняет приведенные в начале статьи веерные кривые – два пути, которыми следуют тонкие пленки при понижении температуры. Но это еще не вся история.
Парадоксы двумерного мира
Оказывается, если параметры системы островков приближаются к порогу перехода между сверхпроводником и изолятором, то в такой пленке развивается огромная диэлектрическая проницаемость – этот хорошо известный специалистам по двухфазным системам факт называется «диэлектрической катастрофой». В результате этого процесса электрическое поле зарядов в пленке оказывается полностью захваченным самой пленкой, и кулоновское взаимодействие в пленке становится двумерным: в отличие от привычного нам трехмерного закона Кулона, где энергия взаимодействия двух зарядов уменьшается обратно пропорционально расстоянию между ними, в двумерном мире кулоновская энергия взаимодействия увеличивается пропорционально логарифму расстояния между зарядами.
ЭФФЕКТ ДЖОЗЕФСОНА И ДЖОЗЕФСОНОВСКАЯ СЕТКА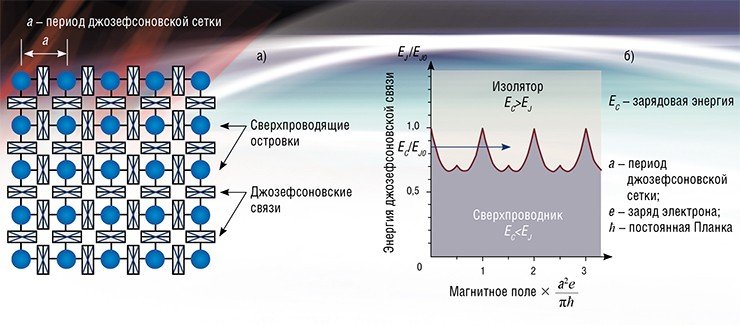
Двумерные сетки джозефсоновских переходов, представляющие массив сверхпроводящих островков, разделенных несверхпроводящим материалом, являются модельными системами для изучения перехода сверхпроводник–изолятор. Свойства таких сеток определяются конкуренцией двух характерных энергий: энергии джозефсоновской связи между двумя соседними островками, EJ0 и зарядовой энергией EC, то есть энергией, необходимой для переноса заряда 2e с одного островка на соседний. В зависимости от соотношения этих энергий EJ0 / EC, сетка джозефсоновских переходов, может находиться в сверхпроводящем состоянии, EJ0 > EC, или в изолирующем, EJ0 < EC.
Заметим, что обе энергии фактически задаются используемыми материалами, геометрическими размерами островков и промежутков между ними.
Однако величиной энергии джозефсоновской связи можно управлять с помощью магнитного поля, что и позволяет наблюдать переход сверхпроводник–изолятор под влиянием магнитного поля при соответственно подобранных параметрах.
К примеру, для квадратной решетки с периодом а, на графике красной линией показана теоретическая зависимость энергии джозефсоновской связи от магнитного поля EJ, приложенного перпендикулярно плоскости решетки в приведенных координатах. Видно, что при некоторых значениях EC, попадающих в область изменения EJ, возможен переход от условия EJ > EC, отвечающего сверхпроводящему состоянию, к выполнению условия EJ < EC, то есть, переход в изолирующее состояние
Двумерность кулоновского взаимодействия позволяет понять аномально большую величину ширины запрещенной зоны, наблюдаемую в наших экспериментах на изолирующих пленках, близких к переходу. Для протекания электрического тока необходимо преодолеть энергию, необходимую для разделение зарядов, – положительный заряд должен двигаться к отрицательному электроду и наоборот. А эта энергия увеличивается в двумерном мире вместе с размерами системы. Но самым удивительным в критических пленках является то, что двумерная кулоновская система претерпевает так называемый переход Березинского–Костерлица–Таулеса (или, как его сокращенно называют, БКТ): при понижении температуры ниже температуры этого перехода положительные и отрицательные заряды связываются в нейтральные диполи, которые не могут двигаться под действием электрического поля. Таким образом, разделение зарядов становится практически невозможным и сопротивление пленки оказывается бесконечно большим, то есть куперовский изолятор с экспоненциально маленькой проводимостью превращается в сверхизолятор.
КУЛОНОВСКОЕ ВЗАИМОДЕЙСТВИЕ В ТРЕХМЕРНОМ И ДВУМЕРНОМ МИРАХ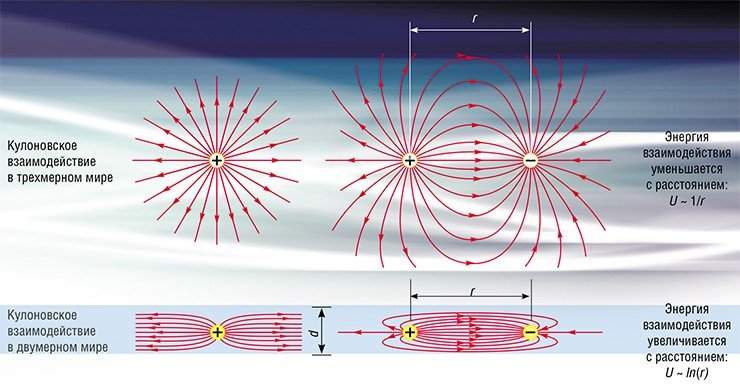
В двумерном мире все меняется кардинально. Представим себе, что все линии электрического поля зажаты в плоскости и не могут ее покинуть. Очевидно, что густота линий увеличится по сравнению с трехмерным миром. Можно строго показать, что в этом случае сила электрического поля будет уменьшаться при удалении от заряда по закону 1/r, то есть значительно медленнее, чем в трехмерном мире. Энергия взаимодействия двух зарядов при этом будет увеличиваться (!) по закону ln(r). На первый взгляд это выглядит парадоксально, но, на самом деле просто непривычно. Главный же вопрос, который здесь возникает: а может ли в принципе реализоваться такая ситуация в нашем трехмерном мире? Ответ: да может, но при весьма специфических условиях. Если заряд помещен в пленку толщиной d с большой диэлектрической проницаемостью ε, то линии электрического поля оказываются зажаты в пленке вплоть до расстояний r ~ εd, и, соответственно, вплоть до этих расстояний реализуется двумерный закон Кулона и логарифмическое увеличение энергии взаимодействия зарядов. На больших расстояниях линии электрического поля начинают выходить на пределы пленки и восстанавливается обычный трехмерный закон Кулона. Таким образом, до тех пор пока размер пленки не превышает εd, энергия, необходимая для растаскивания к краям пленки двух зарядов противоположного знака при протекании тока логарифмически увеличивается с размером пленки
Сверхизолятор оказывается зеркальным образом сверхпроводника. Так как двумерное кулоновское поведение обусловлено наличием сверхпроводяших островков, сверхизолятор также разрушается при температурах и магнитных полях выше критических. Критическое напряжение для сверхизолятора является аналогом критического тока для сверхпроводника. Область существования сверхизолятора изображается фазовой диаграммой дуальной фазовой диаграммы сверхпроводника, а вольт-амперные характеристики сверхпроводника и сверхизолятора являются зеркальными отображениями друг друга. Как и в сверхпроводнике, в сверхизоляторе отсутствуют тепловые потери из-за полной блокировки электрического тока.
ПРОТЕКАНИЕ ТОКА ЧЕРЕЗ МАССИВ СВЕРХПРОВОДЯЩИХ ОСТРОВКОВ, ПОГРУЖЕННЫХ В ИЗОЛИРУЮЩУЮ СРЕДУ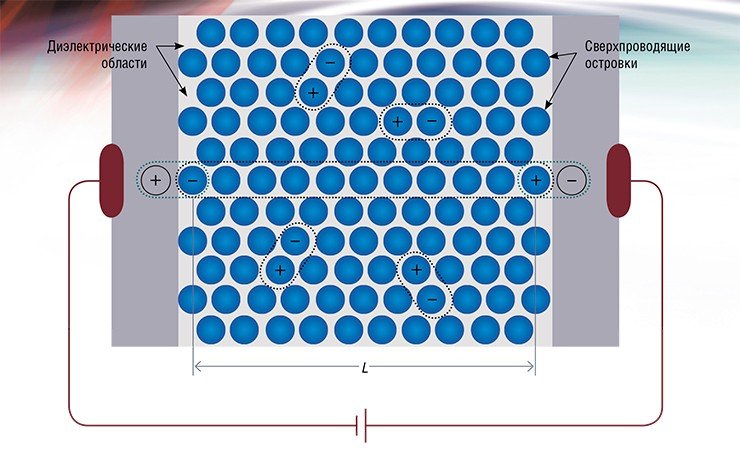
Рассмотрим протекание тока через всю систему, состоящую из источника напряжения, подводящих металлических проводов, контактов к пленке и собственно пленки, представляющей собой массив разделенных сверхпроводящих островков. Будем предполагать, что выполнено условие EJ < EC, и температура ниже температуры зарядового перехода Березинского–Костерлица–Таулеса, то есть все заряды связаны в диполи. Заметим, что в каждый момент времени система является электрически нейтральной. Движение положительного заряда от источника к пленке должно сопровождаться движением навстречу отрицательного заряда внутри пленки и одновременно движением отрицательного заряда от пленки к источнику на другой стороне образца. Такой перенос заряда может происходить только путем расцепления связанных пар положительных и отрицательных зарядов внутри пленки и их разделению к противоположным краям, где заряды аннигилируют со своими зеркальными изображениями в металлических электродах. В силу двумерности кулоновского взаимодействия энергия, необходимая для разделения каждой пары, пропорциональна логарифму размера образца. Можно показать, что в образце размером L эта энергия есть ∆c= EC ln(L/a), где a – размер элементарной ячейки массива. Квантовомеханичекая формула, описывающая такой туннельный ток заряда гласит I~exp (-∆c/W), где W – есть величина, характеризующая потери энергии частицы при туннелировании. Если бы этого процесса (так называемого процесса релаксации энергии) не было, туннелирование было бы невозможно, так как в разных островках энергетические уровни для электронов различны. В массивах островков релаксация происходит путем рождения электронно-дырочных пар, и величина W пропорциональна их количеству. При сравнительно высоких температурах W = T. При низких температурах в двумерных системах электроны и дырки связаны вместе, и создание «свободных» пар, способных поглощать и отдавать любую энергию, становится практически невозможным. Величина W становится экспоненциально большой. Это и есть микроскопический механизм подавления туннельного тока в сверхизолирующем состоянии
Мы пришли к замечательному результату: куперовское спаривание может создавать не только сверхпроводящее состояние, но и его полную противоположность – сверхизолирующее состояние.
Литература
Эдельман В. С. Вблизи абсолютного нуля. Москва: Физматлит, 2001.
Каганов М. И., Лифшиц И. М. Квазичастицы. Москва: Наука, 1989.
Baturina T. I., Strunk C., Baklanov M. R. et al. Quantum Metallicity on the High-Field Side of the Superconductor-Insulator transition // Phys. Rev. Lett. 2007. V. 98, 127003.
Baturina T. I., Mironov A. Yu., Vinokur V. M. et al. Localized Superconductivity in the Quantum-Critical Region of the Disorder-Driven Superconductor-Insulator Transition in TiN Thin Films // Phys. Rev. Lett. 2007. V. 99, 257003.
Vinokur V. M., Baturina T. I., Fistul M. V. et al. Superinsulator and quantum synchronization // Nature. 2008. № 452, P. 613—615.
Sacp B., Chapelier C., Baturina T. I. et al. Disorder-Induced Inhomogeneities of the Superconducting State Close to the Superconductor-Insulator Transition, // Phys. Rev. Lett. 2008. V. 101, 157006.
Chtchelkatchev N. M., Vinokur V. M., Baturina T. I. Hierarchical energy relaxation in mesoscopic tunnel junctions: Effect of a nonequilibrium environment on low-temperature transport // Phys. Rev. Lett. 2009. V. 103, 247003