Теоретики "взвесили" протон

Квантовая хромодинамика (КХД) – раздел физики, изучающий сильное взаимодействие, которое ответственно за образование атомных ядер, состоящих из протонов и нейтронов. В КХД протоны и нейтроны не являются истинно элементарными частицами, а их параметры определяются свойствами составляющих их кварков (фундаментальных частиц) и глюонов (частиц-переносчиков взаимодействия).

Одно из замечательных свойств сильного взаимодействия состоит в том, что сила притяжения между кварками не уменьшается с расстоянием в отличие, например, от силы притяжения электрических зарядов. Это приводит к тому, что кварки и глюоны не наблюдаются поодиночке.

Физики уверены, что уравнения КХД правильно описывают сильные взаимодействия кварков и глюонов. Однако чрезвычайно трудно решить эти уравнения для конкретной кварковой системы, так как для точного расчета, к примеру массы протона, нужно учесть огромное количество возможных состояний кварков и глюонов, образующих протон. Аналитически, т. е. в виде формул, эта задача не решена до сих пор.

Еще в 1974 г. Кеннет Вильсон предложил формулировку квантовой хромодинамики, известную сегодня как КХД на решетках, пригодную для численного компьютерного расчета.

Суть этого подхода заключается в следующем. Непрерывное четырехмерное пространство-время, в котором существуют кварки и глюоны, заменяется на дискретное количество точек, образующих пространственно-временную решетку. В типичных расчетах используются решетки с количеством узлов 32 × 32 × 32 × 32 и более. Для того чтобы получить физические величины, приходится независимо суммировать (интегрировать) по амплитудам полей в каждом узле решетки, т. е. вычислять многомиллионнократные интегралы. Это чрезвычайно ресурсоемкая задача даже для современных компьютеров (для сравнения: при расчете объема трехмерной фигуры необходимо вычислить всего лишь трехкратный интеграл).

С другой стороны, численные расчеты на решетке – это единственный в настоящее время надежный способ получить параметры реально существующих в микромире объектов из фундаментальных физических принципов. В последнее время расчеты на решетках выделились в отдельную отрасль теоретической физики, стремительно развивающуюся с ростом вычислительных возможностей специализированных многопроцессорных компьютерных систем.

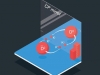
Но я бы не стал называть результаты 2008 г. каким-то особенным прорывом: просто сейчас в расчетах масс сильно взаимодействующих частиц уже достигнута точность лучше 5 %, а для протона – даже 2 %.

Понимание глубинных причин возникновения массы у материи конечно же следует рассматривать как одно из величайших достижений науки. Однако новые знания порождают и новые вопросы. Чтобы убедиться в правильности подхода, мне кажется, недостаточно вычислить величину, которая и так хорошо известна из эксперимента. Настоящим триумфом метода было бы предсказание и последующая экспериментальная проверка плохо известных сегодня параметров частиц. Эта задача требует не только новых расчетов, но и проведения новых прецизионных измерений. Но это уже совсем другая история.