: 17 мар 2006 , Клад тагарского жреца , том 8, №2

Трехмерный мир, в котором мы не живем

Математика — наука, изучающая
количественные и пространственные
формы и отношения действительности
Академик А. Д. Александров

Окружающий нас мир трехмерен. Мы привыкли к этой мысли с рождения — каждый человек знает, что такое высота, длина и ширина, три основных измерения окружающего нас пространства. В зависимости от традиций, принятых в разных странах, размеры предметов измеряют в метрах, футах, ли, лье и других эталонных единицах длины. Для наших дальнейших рассуждений выберем немного необычную единицу длины. Ею будет служить один световой год (1 св. г.), т. е. расстояние, проходимое лучом света за один календарный год. В традиционных мерах длины это составляет невообразимую величину — примерно 9,46•10¹² километров.

Если из окружающего нас пространства мысленно вырезать куб с ребром, равным 1 св. году, то внутри благополучно разместится дом, в котором мы живем, земной шар, Солнечная система… В общем, все, что необходимо для нормальной жизни человека. Для удобства назовем рассмотренный нами куб единичным кубом. А теперь отметим следующий очевидный факт. Несмотря на громадные размеры, наш единичный куб — лишь мельчайшая частица окружающего мира.

Такой воображаемый единичный куб можно вырезать в любой другой точке пространства. При этом можно утверждать, что два куба, вырезанные в разных точках пространства, окажутся одинаковыми. Это и есть основная идея так называемого евклидова многообразия, согласно которой любая его точка окружена кубом соответствующих размеров. Более точно можно сформулировать следующее определение. Трехмерным евклидовым многообразием называется множество М ³, любая точка которого является центром куба, полностью состоящего из точек данного множества.

Кстати сказать, в этом определении размеры самого куба не задаются — вовсе не обязательно использовать кубы больших размеров. С таким же успехом можно утверждать, что каждая точка содержится в кубе, ребро которого не превосходит по длине, скажем, один микрон (10^—6 см).

Все сказанное выше кратко можно выразить следующими словами: окружающий нас мир является трехмерным евклидовым многообразием. А теперь попробуем ответить на следующий вопрос: как устроен мир за пределами единичного куба, в котором находится наш дом — наша Солнечная система?

Трехмерный тор и другие

Если на минуту вообразить, что окружающее нас пространство бесконечно по всем направлениям, то ответ на вопрос о строении окружающего нас мира даст следующая теорема Адамара:

«Бесконечно протяженное по всем направлениям трехмерное евклидово многообразие М ³ совпадает с евклидовым пространством E ³».

Евклидово пространство Е ³ с прямоугольной системой координат всем хорошо известно, поэтому не будем подробно останавливаться на изучении его свойств.

Для того же, чтобы сделать наши рассуждения более содержательными и интересными, предположим другой вариант: окружающий нас мир замкнут, т. е. имеет конечные размеры и не имеет края. Другими словами, зададимся вопросом, как устроены замкнутые трехмерные евклидовы многообразия, или, другими словами, евклидовы формы. Полный ответ на этот вопрос дает теорема, доказанная Дж. Вольфом (1982):

Существует ровно десять трехмерных евклидовых форм. Причем шесть из них представляют собой ориентируемые, а остальные четыре — неориентируемые многообразия.

Все евклидовые формы строятся схожим образом, единственное — для построения некоторых из них нужно использовать куб, а для других — правильную шестиугольную призму.

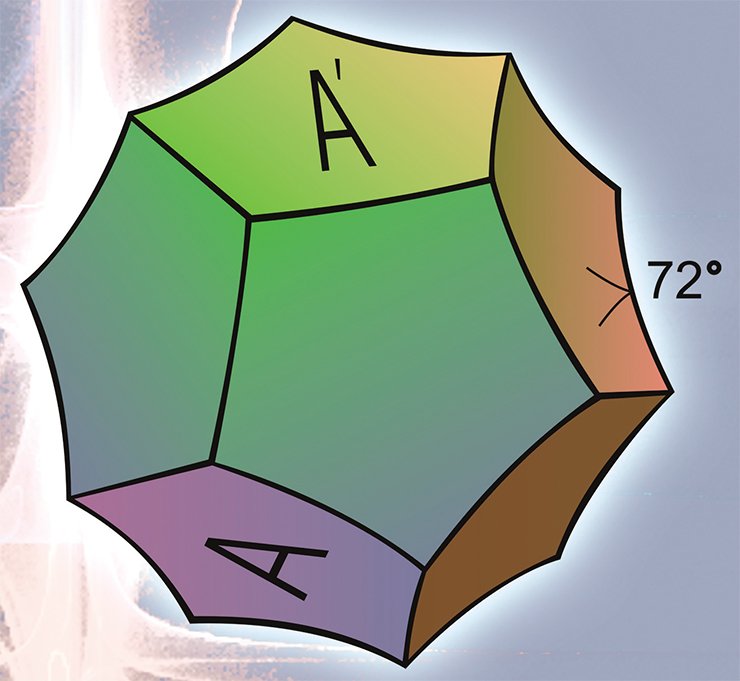
Первой и наиболее известной евклидовой формой является своеобразный аналог знакомого всем двухмерного тора — трехмерный тор. Обозначим это множество (куб с попарно отождествленными гранями) через Т ³. Еще одной евклидовой формой является так называемый скрученный трехмерный тор, обозначенный соответственно как Q ³. А теперь проведем простой физический эксперимент, который покажет, что многообразия Т ³ и Q ³ различны, причем оба отличаются от евклидова пространства Е ³.

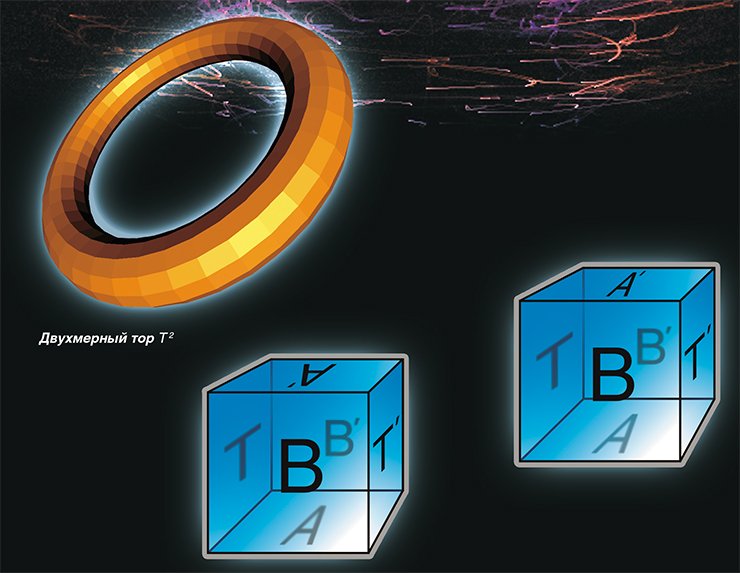
Для этого в центре грани А трехмерного тора поместим космический корабль, летящий со скоростью света, и заставим его стартовать в вертикальном направлении. Ровно через год космический корабль, продолжая двигаться по прямой, вернется в исходную точку. Теперь эта точка будет находиться в центре грани А’, которая, по условию, отождествлена с гранью А. В результате эксперимента обнаружим, что в трехмерном торе Т ³ существует замкнутая прямая линия l длиной в один световой год.

Поставим еще один аналогичный эксперимент. Заставим космический корабль стартовать из точки у, лежащей в грани А на расстоянии 1 км от ее центра. Через год корабль благополучно вернется в точку у. Вывод из второго эксперимента — через точку у проходит замкнутая прямая длиной 1 световой год, параллельная прямой l.

Теперь оба описанных эксперимента проведем в скрученном торе Q ³. Первый эксперимент даст абсолютно тот же самый результат, что и ранее. Однако во втором эксперименте он будет совершенно иным. Корабль, стартующий из точки у, через один год достигнет точки z, которая лежит в грани А’—А и диаметрально противоположна точке у относительно центра этой грани. Полет по прямой продолжится и продлится еще один год, по истечении которого корабль вернется в точку у.

Таким образом, в Q ³ через точку у проходит замкнутая прямая длиной 2, параллельная прямой l. Следовательно, многообразия Т ³ и Q ³ различны, и оба отличаются от пространства Е ³, в котором нет замкнутых прямых линий.

Следующая евклидова форма — заполненная бутылка Клейна (многообразие К ³) — в отличие от предыдущих является неориентируемой. Докажем это. Для этого повторим эксперимент с космическим кораблем, стартующим из центра грани А, но дополнительно снабдим нос корабля пропеллером, с постоянной скоростью вращающимся по часовой стрелке (если наблюдать за ним из кабины пилота). Предположим, что запас топлива у корабля достаточно велик и пропеллер будет вращаться в течение года вплоть до того времени, когда корабль, завершив путешествие по замкнутой прямой l, вернется в исходную точку. В момент, когда корабль вновь окажется в точке старта, пилот с удивлением обнаружит, что пропеллер вращается против часовой стрелки! (Конечно, имеются в виду те часы, которые пилот забыл на старте.) Последнее означает, что многообразие К ³ — неориентируемо и, следовательно, отличается от построенных ранее евклидовых форм Т ³и Q ³.

В заключение заметим, что размеры Солнечной системы (ее диаметр равен примерно 124•10⁹ км) малы по сравнению с размерами многообразий, построенных выше на основе линейного куба. Она может быть расположена как внутри Т ³, Q ³, К ³, так и в любой другой евклидовой формы. При этом для вычисления расстояний, не превосходящих 1 св. год, мы можем пользоваться обычной евклидовой геометрией и даже не догадываться о том, что окружающий нас мир замкнут. В настоящее время человечество не располагает космическими кораблями, летающими со скоростью света. Это означает, что сейчас невозможно осуществить глобальные эксперименты, подобные описанным выше, и, наконец, установить, в каком же из евклидовых миров мы живем.

Многообразные многообразия

Как уже было замечено, все рассмотренные выше многообразия обладают евклидовой геометрией. Что это означает и какие еще геометрии существуют?

Наиболее известными и употребимыми в общечеловеческой практике являются евклидова, сферическая и гиперболическая геометрии. Напомним, что сферическую геометрию иногда называют геометрией Римана, а гиперболическую — геометрией Лобачевского. В трехмерном пространстве, кроме трех указанных, существует еще пять так называемых синтетических геометрий.

В соответствии с тем, какие геометрические законы действуют на трехмерном многообразии, будем называть его соответственно евклидовым, сферическим, гиперболическим или синтетическим.

Евклидовы многообразия мы уже рассмотрели выше. Что до остальных, то более двадцати лет назад У. Терстон (1978) доказал замечательную теорему: почти все трехмерные многообразия являются гиперболическими, то есть подчиняются законам геометрии Лобачевского. За этот результат в 1983 году он был удостоен Филдсовской премии — самой престижной награды для математиков.

Сферические многообразия бывают как трехмерные, так и многомерные (Вольф, 1982). В пространстве любой размерности существует конечное число типов таких многообразий. Синтетических многообразий очень мало (Thurston, 1978; Dunbar, 1981; Терстон, 2001) в отличие от оставшегося класса гиперболических многообразий. Последний неисчерпаемо широк и классификация его к настоящему времени не завершена.

Сферические многообразия

Все трехмерные сферические многообразия — ориентируемы. Это означает, что по какой бы замкнутой траектории не летал космический корабль с непрерывно вращающимся пропеллером, по возвращении в точку старта его пропеллер вращается в ту же сторону, что и в момент старта.

Простейшим сферическим многообразием является трехмерная сфера S ³. Ее можно определить как границу четырехмерного шара или, что то же самое, как множе­ство точек в пространстве Е ⁴, удаленных от центра на одинаковое расстояние. С помощью стереографической проекции можно установить взаимно однозначное и взаимно непрерывное соответствие между точками трехмерной сферы S ³ и точками множества Е ³ + {∞}, полученного добавлением к привычному нам евклидову пространству Е ³ бесконечно удаленной точки ∞. Таким образом можно считать, что S ³ = Е ³ + {∞}.

Вторым примером сферического многообразия служит трехмерное проективное пространство Р ³. Его можно легко представить себе в виде шара, диаметрально противоположные точки которого отождествлены.

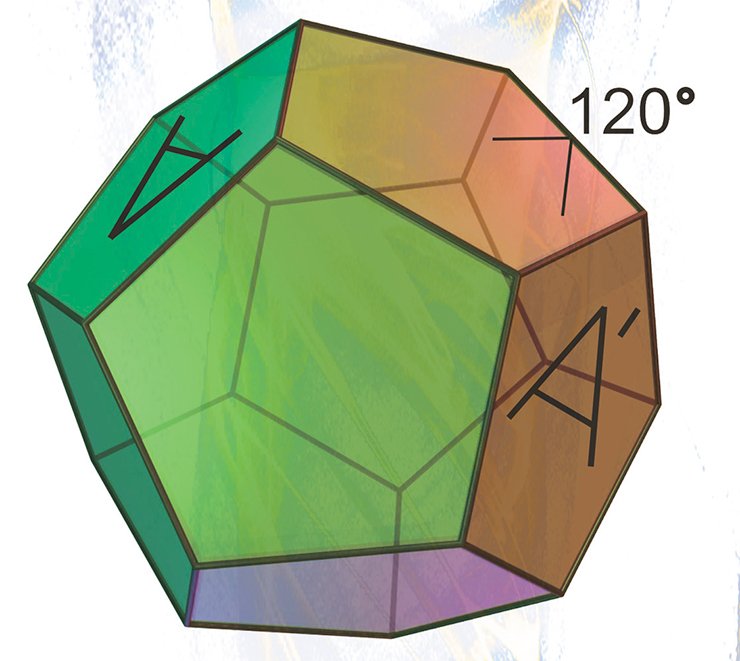
Третий, и пожалуй, самый нетривиальный пример сферического многообразия — сферическое пространство додекаэдра Пуанкаре или, для краткости, сфера Пуанкаре.

Сфера Пуанкаре удивительным образом связана с самыми различными разделами математики — геометрией, топологией, теорией групп, теорией катастроф, теорией узлов и другими (Кирби, Шарлеман, 1982).

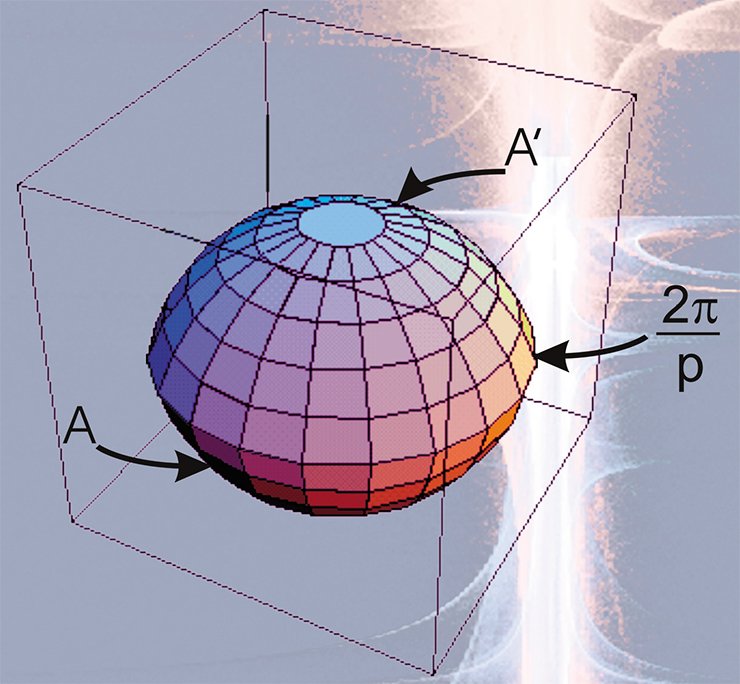
Все остальные сферические многообразия, получаемые по единой схеме, представляют собой так называемые линзовые и призматические пространства.

Гиперболические многообразия

Первое трехмерное замкнутое гиперболическое многообразие было построено немецким математиком Ф. Лебеллем в 1931 г. Однако построение его было достаточно сложным, поэтому двумя годами позже Х. Зейферт и К. Вебер предложили элегантную конструкцию гиперболического пространства додекаэдра.

С точки зрения математики наиболее сложная часть проблемы построения состоит в доказательстве существования этого гиперболического додекаэдра в пространстве Лобачевского. Положительный ответ на этот вопрос дает фундаментальная теорема Е. М. Андреева (1970), в которой сформулированы необходимые и достаточные условия для существования выпуклых гиперболических многогранников. Эта теорема служит одним из краеугольных камней современной теории гиперболических многообразий, созданной У. Терстоном.

Конструируем многообразия из многогранников

Рассмотрим прямоугольный многогранник Р, все двугранные (и плоские) углы которого равны 90°. В евклидовом пространстве в качестве такого многогранника можно взять куб, в сферическом — тетраэдр, а в гиперболическом — шестиугольную призму Лебелля, боковая поверхность которой состоит из 12-ти пятиугольников.

Из теоремы Андреева следует, что любой многогранник, у которого нет треугольных и четырехугольных граней, а в каждой вершине сходится ровно по три ребра, может быть реализован как прямоугольный многогранник в пространстве Лобачевского. Шестиугольная призма Лебелля, очевидно, удовлетворяет этим условиям.

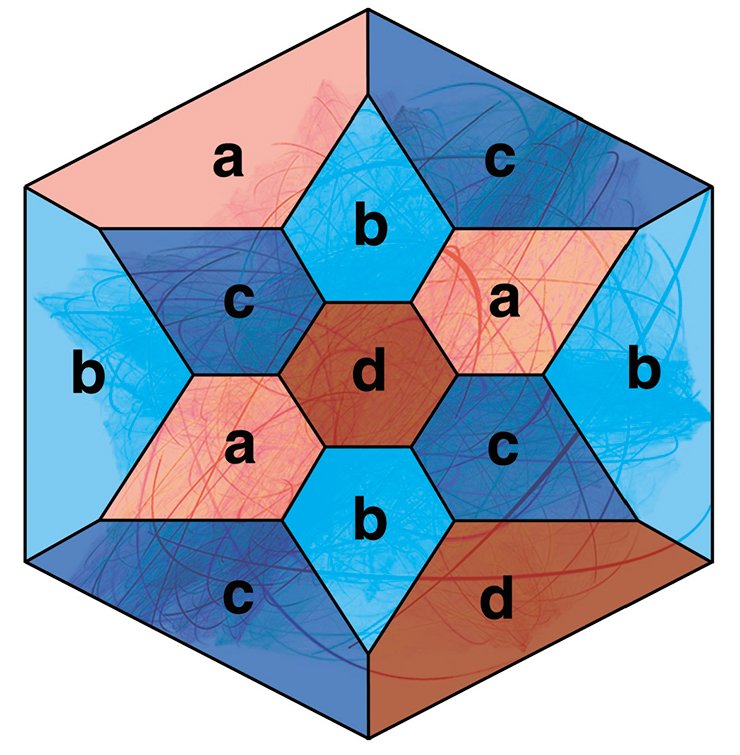
Для построения гиперболических многообразий используется способ, заключающийся в окраске смежных граней многогранника в разные цвета и последующего отождествления соответствующих граней, окрашенных в один цвет, у нескольких одинаковых экземпляров многогранников. Такой способ построения многообразий был впервые реализован Ф. Лебеллем (Loebell, 1931) для шестиугольной призмы, японским математиком М. Такахаши (Takahashi, 1985) — для правильного прямоугольного додекаэдра и А. Ю. Весниным (1987) — для произвольного прямоугольного многогранника Р.

При этом отметим, что все многообразия, построенные по окраске многогранника в четыре цвета, ориентируемы. Однако доказано, что окрашивая грани многогранника Р в пять, шесть или семь цветов, по аналогичной схеме можно построить и неориентируемые многообразия (Mednykh, 1992).

  Остановимся еще на одном свойстве прямоугольных многогранников. Пусть D — правильный прямоугольный додекаэдр в пространстве Лобачевского. Испанский математик Х.-М. Монтезинос (Hilden et al., 1987) доказал следующую замечательную теорему:

«Любое замкнутое трехмерное многообразие может быть получено из конечного числа экземпляров многогранника D попарным отождествлением их граней».

Отметим, что в теореме Монтезиноса все грани склеенных многогранников — конгруэнтны, а все ребра имеют одинаковую длину. При этом каждое ребро окружено четырьмя, двумя или одним додекаэдром. Первую ситуацию легко представить: четыре прямоугольных додекаэдра склеены друг за другом вокруг общего ребра и образуют суммарный угол, равный 4•90° = 360°. Во втором случае пара смежных граней одного додекаэдра отождествляется с парой смежных граней другого додекаэдра. Суммарный двугранный угол вокруг ребра, принадлежащего двум додекаэдрам, в этом случае равен 2•90° = 180°. Третий вариант легко создать, отождествляя смежные грани одного додекаэдра поворотом на угол 90°.

Наличие ребер второго и третьего типа превращает многообразие в многообразие с особенностями, или орбифолд. В этом случае указанные ребра образуют сингулярное множество орбифолда. Заметим, что всюду, кроме сингулярных ребер, многообразие обладает геометрией Лобачевского.

Трехмерные орбифолды

Евклидовы орбифолды

Для всякого трехмерного евклидова орбифолда существует фундаментальное множество — криволинейный многогранник, из которого заданный орбифолд можно получить, попарно отождествляя (склеивая) определенные его грани.

Примерами евклидовых орбифолдов могут служить так называемые Борромеевы кольца или трехмерная сфера с сингулярным множе­ством узел «восьмерка».

Всего существует 230 замкнутых трехмерных евклидовых орбифолдов — по числу кристалло­графических групп, открытых в конце прошлого века русским ученым Е. С. Федоровым. Строение евклидовых орбифолдов было полностью описано в докторской диссертации У. Данбара, защищенной в 1981 г. в Принстонском университете — крупнейшем математическом центре мира.

Сферические орбифолды

Сингулярным множеством сферических орбифолдов может служить так называемый рациональный узел или зацепление. Им может оказаться также заузленный граф, из каждой вершины которого выходит по три ребра. В частности, сингулярным множеством сферического орбифолда будет являться скелет тетраэдра (ребра + вершины), расположенный в трехмерной сфере.

При этом следует иметь ввиду, что сильные заузливания тетраэдра могут испортить сферическую геометрию и заставить орбифолд обладать евклидовой, гиперболической или одной из синтетических геометрий.

Недавно австралийцами профессором К. Ходжсоном и его учеником Д. Хеардом создана компьютерная программа, позволяющая вычислять объемы заузленных графов, вложенных в трехмерную сферу (Hodgson and Heard, 2005). Полная классификация трехмерных орбифолдов во всех геометриях, кроме гиперболической, сделана в работах У. Данбара. Как и в случае многообразий, гиперболическая геометрия является наиболее богатой, и полное описание орбифолдов в ней до сих пор не получено.

Гиперболические орбифолды

  Из теоремы Монтезиноса следует, что каждое трехмерное многообразие может быть превращено в гиперболический орбифолд, если внутрь его поместить подходящее сингулярное множество. Поскольку существует бесконечно много различных многообразий, отсюда следует, что существует также бесконечно много гиперболических орбифолдов.

Один из простейших гиперболических орбифолдов — трехмерная сфера с сингулярным множеством Борромеевы кольца с индексом сингулярности 4. Другой пример — сильно заузленный тетраэдр, все ребра которого имеют индекс сингулярности два. Доказательство таких фактов обычно достаточно сложно и может быть проведено с помощью теорем о геометризации, полученных У. Терстоном, его учениками и последователями. Общий принцип доказательства состоит в следующем: если орбифолд не является евклидовым, сферическим или синтетическим и удовлетворяет некоторым простым геометрическим условиям, то он — гиперболический.

Изменения, произошедшие в математике за последние более чем полтора века, не только необозримо расширили ее содержание, но и изменили его принципиально. В предмет математики сейчас входит любая структура, которую можно исследовать путем логического рассуждения с достаточной строгостью и богатством выводов. Найдет ли она применение и прообраз в действительности — это уже вопрос не к математике.

Понятно, что фактически наибольшее развитие получают те теории, которые находят существенные применения в самой математике и тем более за ее пределами. Хотя опыт развития науки уже достаточное число раз показал, как самые отвлеченные теории находили потом чрезвычайно существенные приложения. Но для самой чистой математики это в принципе безразлично. Лучше всего творческое кредо новой математики выразил создатель теории множеств Г. Кантор, гордо зявив: «Сущность математики... в ее свободе».

Литература

Винберг Э. Б. О неевлидовой геометрии, Соросовский образовательный журнал, № 3, 1996, С. 104—109.

Тёрстон У. Трехмерная геометрия и топология, М: МЦНМО, 2001 (Перевод с англ. под ред. О. В. Шварцмана).

Hodgson C., Heard D. Computer program “Orb”, August 2005, http://www.ms.unimelb.edu.au/~snap/orb.html

Работа поддержана грантом РФФИ (№ 06-01-00153) и INTAS (№ 03-01-3663)

Автор и редакция выражает искреннюю благодарность Н. В. Абросимову (вед. инженеру Института математики им. С. Л. Соболева СО РАН, студенту 6-го курса НГУ), оказавшему неоценимую помощь при подготовке публикации

: 17 мар 2006 , Клад тагарского жреца , том 8, №2