"Воды, в которые я вступаю, не пересекал еще никто" Александр Фридман и истоки современной космологии
Девяносто лет назад российский физик Александр Фридман предсказал, что Вселенная может расширяться или сужаться с ускорением или с замедлением и что она могла даже родиться из «ничего». Эти революционные научные идеи первоначально встретили критику и непонимание со стороны Альберта Эйнштейна, и лишь спустя шесть лет после смерти Фридмана создатель теории относительности признал его правоту и стал его горячим сторонником.
Фридман ушел из жизни рано – в 37 лет. Возможно, именно поэтому титул первооткрывателя расширяющейся Вселенной присваивался попеременно то Жоржу Леметру, то Эдвину Хабблу. Последние астрономические наблюдения подтвердили справедливость одного из сценариев эволюции Вселенной, предсказанного Фридманом, поэтому так важно сегодня напомнить о приоритете нашего соотечественника в этом великом открытии
 В 1922 г. физик из Петрограда Александр Фридман открывает, что уравнения общей теории относительности Эйнштейна допускают не только статические, но и динамические решения. Как следствие, он выводит два дифференциальных уравнения (теперь уравнения Фридмана), описывающих три возможных сценария развития Вселенной. Согласно им Вселенная может сжиматься, расширяться, схлопываться и даже возникать из точки (как говорят физики, из сингулярности). В 1924 г. Фридман предлагает еще одну революционную идею о возможности существования динамической Вселенной с отрицательной кривизной, а значит, бесконечной по объему и неограниченной в пространстве.
В 1922 г. физик из Петрограда Александр Фридман открывает, что уравнения общей теории относительности Эйнштейна допускают не только статические, но и динамические решения. Как следствие, он выводит два дифференциальных уравнения (теперь уравнения Фридмана), описывающих три возможных сценария развития Вселенной. Согласно им Вселенная может сжиматься, расширяться, схлопываться и даже возникать из точки (как говорят физики, из сингулярности). В 1924 г. Фридман предлагает еще одну революционную идею о возможности существования динамической Вселенной с отрицательной кривизной, а значит, бесконечной по объему и неограниченной в пространстве.
Спустя десятилетия космические наблюдения подтвердили, что один из трех сценариев развития космоса, предложенных Фридманом в 1922—1924 гг., оказался соответствующим действительности. Трем американ¬ским астрономам, обнаружившим ускоренное расширение Вселенной, была присуждена Нобелевская премия по физике за 2011 г. При обосновании важности этого открытия Шведская королевская академия наук ссылается на работы Фридмана (Scientific Background on the Nobel Prize in Physics, 2011), но при этом в значительной степени искажает суть его вклада.
К сожалению, непонимание и отрицание с самого начала сопровождали космологические идеи Фридмана, безупречно сформулированные с математической точки зрения. Но время все расставляет по своим местам…
Общая теория относительности: Эйнштейн против де Ситтера
Общая теория относительности предполагает, что гравитационное взаимодействие между физическими телами возникает как результат искривления пространства, вызванного находящимися в нем массами. Ее фундаментальные уравнения связывают кривизну пространства, описываемую тензором четвертого порядка (три пространственных координаты и время), с распределением и потоками массы материи. Математически общая теория относительности представляет собой систему нелинейных дифференциальных уравнений в частных производных, и потому найти ее аналитическое решение можно только для ряда самых простых случаев.

Первое из таких решений, найденное немецким астрономом и физиком Карлом Шварцшильдом в 1916 г., описывает гравитационное поле вокруг массивных тел, таких как Солнце, в частности – движение планет и распространение солнечных лучей. Предельным случаем этого решения является гравитационный коллапс, приводящий к образованию черных дыр.
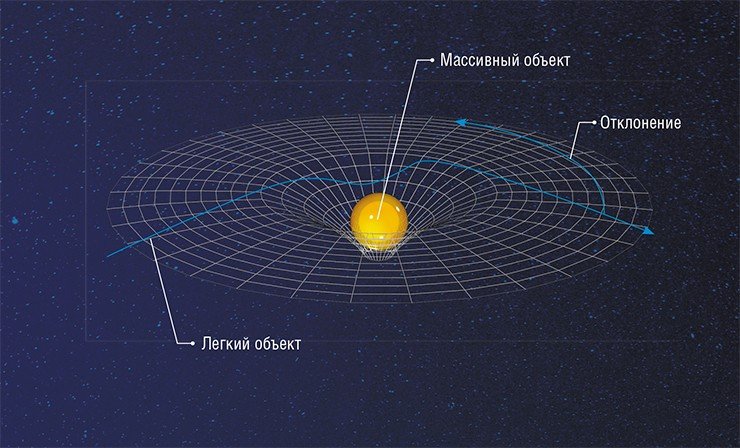
Кривизну трехмерного пространства изобразить наглядно сложнее. Если нарисовать в пространстве координатную сетку, то влияние массы приведет к ее искажению. Тело, которое двигалось бы в неискривленном пространстве вдоль прямых линий сетки, в искривленном пространстве будет двигаться также вдоль этих линий, но теперь они будут уже не прямыми
Вскоре перед физиками встал вопрос: а может ли общая теория относительности описывать саму Вселенную? Для упрощения вычислений был сформулирован следующий основополагающий космологический принцип: Вселенная однородна (т. е. любой наблюдатель видит сходную картину) и изотропна (по любому направлению Вселенная одинакова). Были выдвинуты и менее важные предположения: что плотность материи одинакова во всех точках пространства, что скорости движущихся тел ничтожны по сравнению со скоростью света и что иного взаимодействия, кроме гравитационного, между телами не существует.
И действительно, куда бы астрономы ни направляли свои телескопы, они всегда видели схожую картину. Кроме того, наибольшие скорости звезд относительно Солнца, известные в то время, были не больше 5 км/c.
В феврале 1917 г. Эйнштейн находит первое из таких космологических решений: в его модели Вселенная представляется трехмерной гиперсферой постоянного радиуса кривизны, не меняющегося со временем. Для того чтобы Вселенная не схлопывалась под действием сил собственного гравитационного притяжения, Эйнштейн вводит в свои уравнения еще один член с коэффициентом Λ, названный космологической постоянной. На основе известных на то время астрономических данных его теория оценивала радиус Вселенной в 800 млн световых лет.
 Эйнштейну кажется, что цель достигнута. Но второе космологическое решение, найденное нидерландским астрономом Виллемом де Ситтером буквально месяц спустя, действует на Эйнштейна как холодный душ. Вселенная де Ситтера также статична, но в ней каждый наблюдатель окружен своего рода «горизонтом», где время замедляется и даже останавливается. Кроме того, в этой модели Вселенной не были «предусмотрены» такие реалии, как материя и излучение.
Эйнштейну кажется, что цель достигнута. Но второе космологическое решение, найденное нидерландским астрономом Виллемом де Ситтером буквально месяц спустя, действует на Эйнштейна как холодный душ. Вселенная де Ситтера также статична, но в ней каждый наблюдатель окружен своего рода «горизонтом», где время замедляется и даже останавливается. Кроме того, в этой модели Вселенной не были «предусмотрены» такие реалии, как материя и излучение.
Из-за последнего обстоятельства Эйнштейн объявляет модель де Ситтера неприемлемой, поскольку она противоречит принципу Эрнста Маха, гласящему, что инертность и инерция (следовательно, и опирающиеся на инертные свойства вещества принципы общей теории относительности) не могут существовать без материи. Однако у модели де Ситтера было одно важное достоинство: при замедлении времени у «горизонта» возникает псевдодоплеровский эффект, с помощью которого можно было бы объяснить факт смещения в красную сторону линий в спектре удаленных галактик, открытый в 1914 г. американским астрономом Весто Слайфером (обсерватория Лоуэлла, Аризона).
Де Ситтер оценил радиус Вселенной в 4,5 млн световых лет. Но эта цифра уже тогда казалась невозможно малой, ведь существующий в то время телескоп американской обсерватории Маунт Вильсон был способен различать объекты, находящиеся на расстоянии до 150 млн световых лет!
КОРОТКАЯ, НАПОЛНЕННАЯ ЖИЗНЬНачавшаяся в августе 1914 г. Первая мировая война прерывает его научные занятия, и Фридман отправляется добровольцем на австрийский фронт, где служит в авиации, в роли инструктора по баллистике. Он составляет таблицы для прицельного бомбометания, принимает участие в разведывательных полетах. За храбрость во время боевых действий Фридман награжден Георгиевским крестом и произведен в офицеры.
После Февральской революции в России создаются новые университеты в провинции, и Фридман в 1918 г. по рекомендации Стеклова получает свое первое профессорское место в Перми. Там он преподает несколько прикладных дисциплин. В 1919-м эвакуируется с гуманитарной частью университета вместе с отступающей армией Колчака, но вскоре меняет свое решение и в Екатеринбурге поворачивает назад.
В 1920 г. Фридман возвращается в Петроград и начинает работать в геофизической обсерватории, а через пять лет становится ее директором. Основной его интерес в то время сосредоточен на аэродинамике и теории турбулентности. Параллельно он также преподает механику в Петроградском политехническом институте и интересуется общей теорией относительности и квантовой теорией. В 1924 г. Фридман выступает с докладом на I нтернациональном конгрессе по механике в Дельфте (Нидерланды), его работами интересуются Леви-Чивита, Курант и другие лучшие математики Европы. Он принимает активное участие в подготовке собрания сочинений недавно умершего академика А. М. Ляпунова. О научном энтузиазме и энергии Фридмана говорит такой факт, что в июле 1925 г. он участвует в рискованном полете на стратостате с целью сбора данных о состоянии атмосферы на больших высотах. Достигнув высоты 7400 метров, он сам и пилот Федосеенко оказываются на волосок от гибели из-за нехватки кислорода. Чрезвычайно любопытны воспоминания обоих участников об этом полете, опубликованные уже после смерти Фридмана в журнале «Хочу все знать».
Появившаяся в 1905 г. специальная теория относительности была хорошо известна в России. Но статья Эйнштейна, написанная 1915 г., в которой он сформулировал принципы общей теории относительности, из-за Первой мировой войны дошла до российских ученых с запозданием. Вскоре после окончания войны сообщения об этой теории и о подтверждающих ее наблюдениях Артуром Эддингтоном солнечного затмения в мае 1919 г. наконец дошли до России и были с энтузиазмом восприняты научной общественностью.
С 1921 г. возобновляется доставка европейских научных публикаций в Россию и российские ученые получают доступ к необходимой литературе. Кроме того, ценную информацию о новой теории привозит в Петроград физик Всеволод Фредерикс, знавший о ней фактически из первых рук. Во время войны он был интернирован в Германию в качестве «гражданского пленного». По разрешению немецких властей Фредерикс работал в Геттингене ассистентом у Давида Гильберта, сформулировавшего в начале 1916 г. уравнения общей теории относительности независимо от Эйнштейна, и был очень хорошо знаком с ее принципами.
В тесном сотрудничестве с Фредериксом Фридман и создает свои основополагающие труды по общей теории относительности.
К несчастью, жизнь Александра Фридмана обрывается в самом ее разгаре – в сентябре 1925 г. он заболевает брюшным тифом по возвращении из Крыма, и после двух недель борьбы с недугом умирает в возрасте 37 лет
И все же модель де Ситтера еще долго оставалась в центре внимания космологов. В работах Феликса Клейна, Корнелия Ланцоша и Жоржа Леметра рассматривались ее варианты в зависимости от выбора системы координат: в виде шарового мира (пространство – время) с постоянной положительной кривизной или даже плоского мира с экспоненциально увеличивающимся масштабом пространства. А в 1923—1924 гг. оценка спектрального смещения в модели де Ситтера была улучшена Германом Вейлем и Людвиком Зильберштейном.
Все эти идеи широко обсуждаются вплоть до 1930 г. Участники дискуссии практически не замечают абсолютно новой, революционной идеи, привнесенной аутсайдером из далекого революционного Петрограда.
Вселенная Фридмана: три сценария эволюции
В своей первой работе, датированной 29 мая 1922 г., Фридман ссылается на описанные выше работы Эйнштейна и де Ситтера. Но вместо того, чтобы выбирать между двумя статическими моделями, он рассматривает задачу поиска космологического решения уравнений общей теории относительности с более общих позиций.

Так же, как и Эйнштейн, Фридман представлял себе пространство в виде трехмерной гиперсферы. Однако в отличие от Эйнштейна он понимал, что однородная и изотропная Вселенная не обязательно должна быть статичной и что радиус кривизны пространства R может меняться во времени. В этом случае существует два класса решения уравнений общей теории относительности – статические и динамические. К первым относятся модели Эйнштейна и де Ситтера; ко вторым – Фридмана, который приходит к двум обыкновенным дифференциальным уравнениям для радиуса кривизны как функции времени.
В этом случае радиус кривизны получается путем обращения некоторого эллиптического интеграла, т. е. путем решения относительно R уравнения:
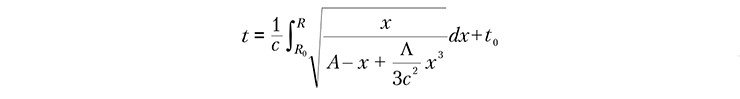
В этом выражении, R0 – это нынешний радиус Вселенной, а t0 – это «время прошедшее от сотворения мира» (по собственному выражению Фридмана).
Космологическая постоянная Λ так же, как и у Эйнштейна, входит в уравнения Фридмана, но она играет роль независимого параметра, который должен быть определен эмпирически. Оказывается, что в зависимости от соотношения между Λ и средней плотностью вещества во Вселенной возникают три главных сценария эволюции Вселенной.
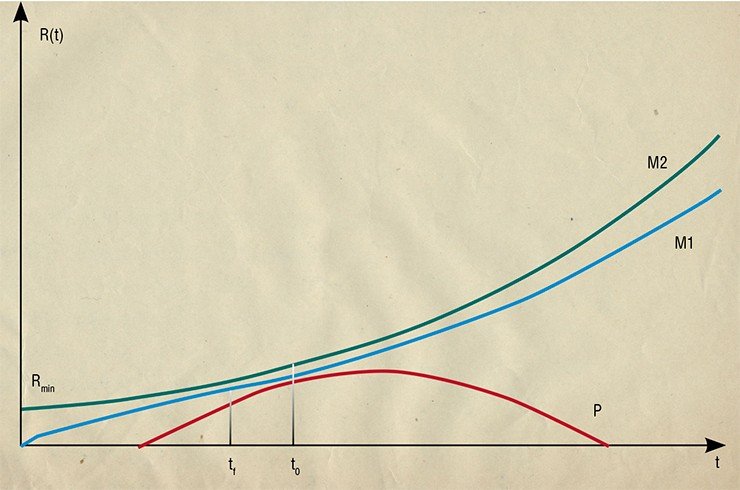
Если космологическая постоянная Λ будет больше некоторой критической величины, зависящей от плотности вещества, то Вселенная возникает из сингулярности (точки), где ее радиус равен нулю. Через некоторое время быстрое первоначальное расширение замедляется, и с некоторого момента начинается фаза расширения с ускорением, когда радиус Вселенной R(t) растет экспоненциально со временем. Фридман называет этот сценарий «монотонным миром первого рода» (М1). Его характерная черта – особая точка перехода от фазы замедления к фазе ускорения.

Метрика пространства это функция, при помощи которой можно определить расстояние между двумя бесконечно близкими точками. Например, для евклидовой плоскости она определяется как dr2=dx2+dy2, а для поверхности двумерной сферы радиуса R - dr2=R2(dθ2+sin2θ•dφ2), где θ (широта) и φ (долгота) – угловые координаты на сфере. Аналогично определяется метрика трехмерной сферы: радиус сферы (R) может рассматриваться как радиус кривизны пространства. В модели Эйнштейна радиус R постоянен, в то время как в модели Фридмана он зависит от времени
Если же космологическая постоянная меньше той же критической величины, то возможны два сценария. При положительном значении Λ Вселенная в начальный момент имеет конечный радиус, а затем безгранично расширяется с ускорением. Фридман назвал этот сценарий «монотонным миром второго рода» (М2).

Другой сценарий особенно интересен: он может реализоваться и при отрицательном значении космологической постоянной. В этом случае Вселенная возникает из сингулярности, а затем расширяется. Скорость расширения постоянно уменьшается и через некоторое время она начинает сжиматься со все возрастающей скоростью, пока не схлопывается обратно в сингулярность.
Время жизни такого мира конечно и его существование завершается событием, прямо противоположным Большому взрыву – Большим схлопыванием. Такой мир Фридман назвал периодическим, ведь процесс расширения и схлопывания может происходить бесконечное число раз. Фридман оценил период в 10 млрд световых лет, что на удивление близко к современным оценкам времени, прошедшего с момента Большого взрыва.

Фридман также описывает и два предельных сценария своей модели в случае, когда космологическая постоянная Λ равна критическому значению. В одном из них Вселенная расширяется с замедлением, асимптотически приближаясь к размеру статичной модели Эйнштейна; в другом она начинается с размера статической модели Эйнштейна и затем бесконечно долго «уходит» от него, расширяясь по экспоненте.
Фридман и Эйнштейн
В книге «Мир как пространство и время», увидевшей свет в 1923 г., Фридман суммирует свои результаты, рассказывая о Большом взрыве совершенно современным языком: «Переменный тип Вселенной представляет большое разнообразие случаев; для этого типа возможны случаи, когда радиус кривизны мира, начиная с некоторого значения, постоянно возрастает с течением времени; возможны далее случаи, когда радиус кривизны меняется периодически: Вселенная сжимается в точку (в ничто), затем снова из точки доводит радиус свой до некоторого значения, далее опять, уменьшая радиус своей кривизны, обращается в точку и т. д.
Невольно вспоминается сказание индусской мифологии о периодах жизни, появляется возможность также говорить о «сотворении мира из ничего», но все это пока должно рассматриваться как курьезные факты, не могущие быть солидно подтвержденными недостаточным астрономическим материалом. Бесполезно за отсутствием надежных астрономических данных приводить какие-либо цифры, характеризующие «жизни» переменной Вселенной; если все же начать подсчитывать ради курьеза время, прошедшее от момента, когда Вселенная создавалась из точки, до теперешнего ее состояния, начать определять, следовательно, время, прошедшее от создания мира, то получатся числа в десятки миллиардов наших обычных лет».
 В июне 1922 г. Фридман посылает русскоязычный вариант своей работы в Лейден, нидерландскому физику-теоретику Паулю Эренфесту, который передает для публикации в центральный немецкий «Физический журнал» (Zeitschrift für Physik). На статью, вышедшую в свет в июле 1922 г., обращает внимание сам Эйнштейн, что, впрочем, неудивительно – ведь Эренфест был близким другом создателя теории общей относительности.
В июне 1922 г. Фридман посылает русскоязычный вариант своей работы в Лейден, нидерландскому физику-теоретику Паулю Эренфесту, который передает для публикации в центральный немецкий «Физический журнал» (Zeitschrift für Physik). На статью, вышедшую в свет в июле 1922 г., обращает внимание сам Эйнштейн, что, впрочем, неудивительно – ведь Эренфест был близким другом создателя теории общей относительности.
Оценка Эйнштейном теории Фридмана как «подозрительной» показала, насколько неприемлемой в то время выглядела для него идея об изменяющейся Вселенной. Правильная, по его мнению, теория должна была подтвердить «очевидное» постоянство космоса.
В сентябре 1922 г. Эйнштейн посылает в Zeitschrift für Physik короткую заметку, в которой высказывает предположение, что Фридман допустил математическую ошибку. В ответном письме, датированном декабрем 1922 г., Фридман приводит свои выкладки более подробно. Однако это письмо попадает в руки адресата только в мае следующего года, когда Эйнштейн возвращается из своего лекционного турне вокруг света.
Месяцем позже коллега Фридмана советский физик Юрий Александрович Крутков встречается с Эйнштейном в доме Эренфеста в Лейдене и дает последние разъяснения. Сразу же после этой встречи Эйнштейн публикует в Zeitschrift für Physik еще одно сообщение, в котором признает математические выкладки Фридмана верными. Правда, в черновике он все-таки отмечает, что «решение не имеет физического смысла», но, поразмыслив, вычеркивает неосторожную ремарку.
Тем не менее должно было пройти еще восемь лет, прежде чем Эйнштейн согласился с идеей расширяющейся Вселенной.
В поиске бесконечной Вселенной
Фридман с самого начала понимал, что геометрию, топологию и кинематику реальной Вселенной невозможно определить, исходя лишь из уравнений общей теории относительности, и что выбор одного из нескольких возможных космологических решений должен основываться на астрономических наблюдениях.
 Однако более всего он был озабочен представлением о конечности Вселенной, к тому времени уже прочно укоренившемся в умах физического сообщества благодаря авторитету Эйнштейна. Поэтому в своих работах 1922—23 гг. Фридман настаивает, что локальная метрика пространства сама по себе не может однозначно определять глобальные свойства (и, в частности, конечность) Вселенной. Для начала он предлагает довольно-таки умозрительную алгебротопологическую конструкцию бесконечного пространства со сферической метрикой.
Однако более всего он был озабочен представлением о конечности Вселенной, к тому времени уже прочно укоренившемся в умах физического сообщества благодаря авторитету Эйнштейна. Поэтому в своих работах 1922—23 гг. Фридман настаивает, что локальная метрика пространства сама по себе не может однозначно определять глобальные свойства (и, в частности, конечность) Вселенной. Для начала он предлагает довольно-таки умозрительную алгебротопологическую конструкцию бесконечного пространства со сферической метрикой.
Конструкция из алгебраической топологии была впервые использована в космологии в 1900 г. немецким астрономом Шварцшильдом, а позже, в 1917 г., де Ситтером под именем эллиптическое пространство (сейчас более известное как вещественное проективное пространство). В любой размерности оно представляет собой гиперсферу, в которой точки-антиподы отождествлены. Другими словами, это пространство всевозможных направлений из любой точки евклидова пространства, с размерностью на единицу больше.
Так как на гиперсфере любой источник света виден с двух противоположных сторон, то можно вполне ограничиться одной только половинкой сферы. Вещественное проективное пространство в нечетных размерностях (в частности, в размерности три) не только сохраняет метрику гиперсферы, но и ориентируемо так же, как и сама гиперсфера. Вот только его объем будет в два раза меньше, чем у гиперсферы, и масса такой Вселенной будет соответственно в два раза меньше, чем масса сферической Вселенной с той же плотностью материи.
 На семинаре Эренфеста Фридман познакомился с теорией накрытий римановых многообразий, которая была сформулирована Анри Пуанкаре в начале 1900-х гг. Вдохновленный этой теорией, Фридман предлагает вариант бесконечного пространства со сферической метрикой, которое можно получить, «накрывая» гиперсферу бесконечным евклидовым пространством той же размерности. В одномерном случае это эквивалентно «накрытию» конечной окружности бесконечной прямой, представляющей собой бесконечно тонкую и бесконечно длинную обмотку окружности. При этом у окружности и у обмотки будет одна и та же метрика, но каждая точка окружности будет «накрыта» бесконечным количеством точек прямой. Однако в случае двух- и трехмерного пространства эта процедура не позволяет получить физически корректное пространство: полюса гиперсферы остаются при этом не «накрытыми», а в реальной Вселенной такая неоднородность не наблюдается.
На семинаре Эренфеста Фридман познакомился с теорией накрытий римановых многообразий, которая была сформулирована Анри Пуанкаре в начале 1900-х гг. Вдохновленный этой теорией, Фридман предлагает вариант бесконечного пространства со сферической метрикой, которое можно получить, «накрывая» гиперсферу бесконечным евклидовым пространством той же размерности. В одномерном случае это эквивалентно «накрытию» конечной окружности бесконечной прямой, представляющей собой бесконечно тонкую и бесконечно длинную обмотку окружности. При этом у окружности и у обмотки будет одна и та же метрика, но каждая точка окружности будет «накрыта» бесконечным количеством точек прямой. Однако в случае двух- и трехмерного пространства эта процедура не позволяет получить физически корректное пространство: полюса гиперсферы остаются при этом не «накрытыми», а в реальной Вселенной такая неоднородность не наблюдается.
Параллельно Фридман выдвигает еще один аргумент против идеи о замкнутом космосе. По предложению своего давнего друга математика Якова Тамаркина он задается вопросом: имеются ли у уравнений общей теории относительности решения в виде бесконечного по объему гиперболоида с одинаковой отрицательной кривизной в каждой точке пространства?
В своей новой статье, опубликованной в Zeitschrift für Physik в январе 1924 г., он приводит два таких решения: статическое и динамическое. Статическое решение для пространства с отрицательной кривизной, как и решение де Ситтера, требует нулевой плотности вещества во Вселенной, а значит, не представляет физического интереса. В случае динамического решения плотность материи должна быть такой же, как и в варианте с положительной кривизной. Из чего, например, следует, что невозможно определить знак кривизны пространства на основе одного лишь измерения плотности вещества.
Эта статья Фридмана также была проигнорирована международным физическим сообществом, включая Эйнштейна.
По следам Фридмана: открытия Жоржа Леметра
Дальнейшая судьба теории Фридмана оказалась далеко не «линейной». Вскоре она была переоткрыта заново и обогащена новыми идеями, главные из которых касались «темной материи» и «постоянной Хаббла».
В 1927 г. бельгийский физик и священник Жорж Леметр переоткрывает уравнения Фридмана и решает их. Зная результаты Слайфера относительно преобладания красного смещения в спектре галактик, он приходит к пониманию, что Вселенная, скорее всего, расширяется. Поэтому он называет свою работу «Об однородной Вселенной с постоянной массой и увеличивающимся радиусом». Но вместо того, чтобы рассмотреть всевозможные сценарии, он выбирает предельный случай монотонного мира – М2 по классификации Фридмана, в котором размер Вселенной логарифмически медленно возрастает от радиуса Эйнштейна до бесконечности. Этот сценарий, как потом выяснилось, не является физически состоятельным.
Зато в другом вопросе Леметр идет дальше Фридмана, связав математику с астрономией. Фридман не знал о результатах Слайфера, опубликованных в 1923 г., тогда как Леметр получил их, как говорится, из первых рук: в 1925 г. он много путешествовал по Америке, посещая все астрономические обсерватории.
Леметр делает элегантную оценку величины «красного смещения» из своей теории и выводит важное соотношение:
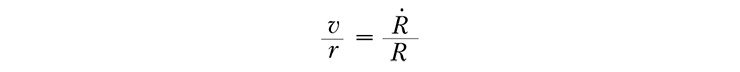
где v – скорость галактики, r – расстояние до нее, R – радиус кривизны пространства и Ṙ – скорость изменения радиуса кривизны.
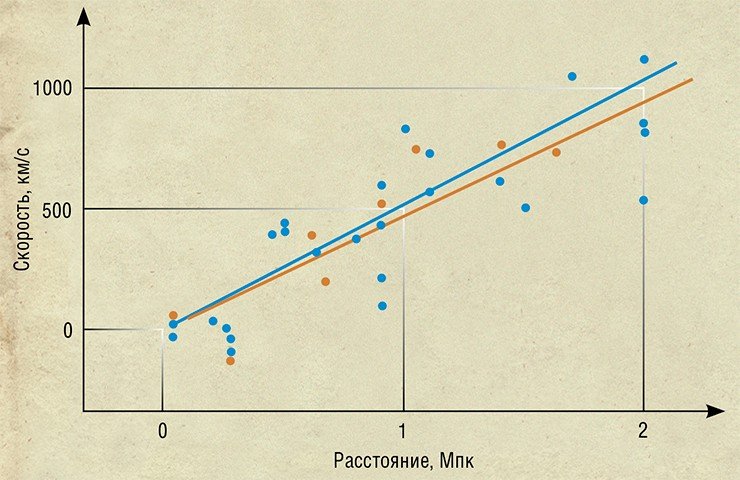
Поскольку в модели Леметра радиус увеличивается со временем почти по экспоненте, то правая часть уравнения близка к постоянной величине. Это означает, что скорости галактик должны быть пропорциональны расстоянию до них с одним и тем же постоянным коэффициентом. Леметр сравнивает скорости 42-х спиральных галактик, вычисленные Слайфером, с расстояниями до них, определенными американским астрономом Эдвином Хабблом, и получает искомую постоянную, равную 625 км/сек/Мпк.
Выбери Леметр другой сценарий расширения Вселенной – от сингулярности, он мог бы оценить «время от сотворения мира». Но в результате оценивает лишь то, что может, т. е. первоначальный радиус Вселенной.
Леметра, опубликовавшего свои открытия в малоизвестном журнале Бельгийской академии наук, ждала судьба Фридмана: никто из корифеев, даже его бывший учитель Артур Эддингтон, не проявляет интереса к его идеям. На конференции в Сольвее в 1927 г. Эйнштейн сообщил Леметру, что Фридман уже получил эти решения раньше, и назвал идею расширяющейся Вселенной «abominable» (буквально: «отвратительной»).
Великий перелом: звездный час Эдвина Хаббла
В 1929 г. Хаббл оценивает с помощью специальной техники расстояния до 46 галактик и, располагая на графике их скорости, полученные Слайфером, в зависимости от своих расстояний до них, обнаруживает, что полученные точки лежат достаточно близко от прямой. Наклон этой прямой, вычисленный как 530 км/сек/Мпс (сплошная прямая на графике), и получает название постоянной Хаббла.
На заседании Английского астрономического общества в январе 1930 г. Эддингтон и де Ситтер признают, что модель де Ситтера не в состоянии объяснить обнаруженную линейную зависимость между расстояниями до галактик и их скоростями. Тогда Леметр обращает внимание Эддингтона на свою работу 1927 г., и тот воспринимает идею расширяющейся Вселенной как откровение. Следующим был де Ситтер, заявивший, что «наконец-то пелена спала с его глаз».

Дольше всех противится новой теории Эйнштейн, но и его мнение постепенно меняется, чему способствуют публикация результатов Хаббла и найденное Эддингтоном в том же году доказательство нестабильности статического решения самого Эйнштейна, даже при наличии положительной космологической постоянной.
В начале 1931 г. Эйнштейн отправляется в калифорнийскую обсерваторию Маунт Вильсон, чтобы лично поговорить с Хабблом и обсудить его результаты. Вернувшись в Берлин, он пишет работу, где признает теорию расширения Вселенной, отмечая приоритет Фридмана, и предлагает исключить из общей теории относительности своего давнего «недруга» – космологическую постоянную Λ.
До открытия того факта, что расширение Вселенной происходит с ускорением, оставалось еще почти полстолетия. Неудивительно, что Эйнштейн полагал, что модель расширяющейся Вселенной – решение, вытекающее из теории Фридмана при нулевом значении космологической постоянной, является единственно верным описанием Вселенной.
В аппендиксе «О космологической проблеме», добавленном к основному тексту своего известного сборника лекций «The Meaning of Relativity» (1946), Эйнштейн отметит: «…математик Фридман нашел способ решить эту проблему [космологической постоянной]. Его результаты нашли неожиданное подтверждение в открытом Хабблом расширении звездной системы *. Дальнейшее изложение есть не что иное, как изложение идеи Фридмана…». И затем на 15 страницах Эйнштейн подробно объясняет теорию Фридмана.
В 1932 г. Эйнштейн и де Ситтер напишут совместную работу, где предложат исключить из общей теории относительности не только космологическую постоянную, но и идею об искривленной Вселенной, предлагая рассматривать только плоскую модель. Именно такая модель и станет основной для теории расширяющейся Вселенной на целые десятилетия вперед, и почти до конца века учебники по космологии будут разве что в примечаниях обсуждать модели с ненулевой космологической постоянной.
С другой стороны, с помощью астрономических наблюдений пока не удалось обнаружить ни одного доказательства того, что Вселенная в космических масштабах отличается от неискривленного евклидова пространства. Однако не исключено, что более точные измерения еще выявят ее положительную или отрицательную кривизну, предсказанную Фридманом.
По сценарию Фридмана
В конце своей книги Фридман (1923 г.) напишет: «Теория Эйнштейна оправдывается на опыте; она объясняет старые, казавшиеся необъяснимыми явления и предвидит новые поразительные соотношения. Вернейший и наиболее глубокий способ изучения при помощи теории Эйнштейна геометрии мира и строения нашей Вселенной состоит в применении этой теории ко всему миру и в использовании астрономических исследований. Пока этот метод немногое может дать нам, ибо математический анализ складывает свое оружие перед трудностями вопроса, и астрономические исследования не дают еще достаточно надежной базы для экспериментального изучения нашей Вселенной. Но в этих обстоятельствах нельзя не видеть затруднений временных; наши потомки, без сомнения, узнают характер Вселенной, в которой мы обречены жить...»
 Сам Фридман особенно выделял периодический мир. Циклические рождения и исчезновения Вселенной напоминали ему философские идеи о реинкарнации, идущие из Индии и Древней Греции. Но благодаря авторитету Эйнштейна среди космологов с 1930-х гг. главным фаворитом стала плоская Вселенная, расширяющаяся до бесконечности с замедлением (т. к. при отсутствии космологической постоянной ничто не противодействует силе гравитации, препятствующей ускорению плоского мира).
Сам Фридман особенно выделял периодический мир. Циклические рождения и исчезновения Вселенной напоминали ему философские идеи о реинкарнации, идущие из Индии и Древней Греции. Но благодаря авторитету Эйнштейна среди космологов с 1930-х гг. главным фаворитом стала плоская Вселенная, расширяющаяся до бесконечности с замедлением (т. к. при отсутствии космологической постоянной ничто не противодействует силе гравитации, препятствующей ускорению плоского мира).
Правда, уже с 1980-х гг. среди теоретиков стали раздаваться голоса в пользу подхода Леметра, утверждавшего, что космологическая постоянная Λ помогает разрешить ряд трудностей, стоящих перед теорией. И все же полученные в 1998—1999 гг. результаты астрономических наблюдений оказались настоящим сюрпризом для научного сообщества.
Изучая яркость сверхновых звезд класса 1а, удаленных от нас на 5 млрд световых лет, две независимые команды астрономов во главе с тремя будущими лауреатами Нобелевской премии Солом Перлмуттером, Адамом Риссом и Брайаном Шмидтом – обнаружили ускорение Вселенной за этот период. Это означало, что периодический мир Фридмана должен быть отвергнут. Кроме того, обе группы выяснили, что космологическая постоянная достаточно велика, и установили соотношение количества энергии материи (включая темную материю) и темной энергии в теперешней Вселенной, равное 30 % и 70 %, соответственно.
Однако эти результаты еще не давали возможности точно определить, какой из двух монотонных сценариев Фридмана реализуется – с сингулярностью или с конечным радиусом Вселенной в начале времен.
Сделать этот выбор удалось благодаря особенности первого сценария, состоявшей в том, что ускорение расширения Вселенной сначала уменьшается, а затем растет. Если принять возраст Вселенной в 13,75 млрд лет, как это определяется из современного значения постоянной Хаббла, и соотношением между энергией материи и темной энергией, то оказывается, что точка перемены знака ускорения отстоит от нас на 5,5 млрд световых лет.
В 2004 г. команде Рисса удалось измерить расстояние до сверхновой звезды, вспыхнувшей в эпоху замедления расширения Вселенной, которая удалена от нас на 8 млрд световых лет. Эти результаты свидетельствуют, что примерно 5 ± 1 млрд световых лет назад замедление расширения Вселенной действительно сменилось ускорением.
Таким образом, первым к финишу пришел сценарий монотонного мира М1 Фридмана.
Кто первый?
После публикации сенсационных астрономических результатов в 1998—1999 гг. историки науки начали спор о приоритете в открытии теории Большого взрыва. После непродолжительной дискуссии в «финал» вышли Леметр и Хаббл, причем последний считался фаворитом – именно ему одному приписывалась идея расширяющейся Вселенной. Но неожиданно выяснилось, что сам Хаббл никогда не верил в эту теорию.
В центр дискуссии попала одна загадочная история. Статья Леметра 1927 г. была переведена в 1931 г. и напечатана в журнале Английского астрономического общества, однако в этой перепечатке был опущен большой, размером со страницу, фрагмент с выводом постоянной Хаббла из астрономических данных. Возникло мнение, что именно Хаббл лично или через друзей был цензором статьи Леметра. Однако недавно была доказана полная несостоятельность этой версии: было найдено письмо Леметра к редактору английского журнала, в котором он сам соглашается удалить этот кусок, как устаревший (Livio, 2011).
Но историки уже объявили Леметра автором постоянной Хаббла и победителем в споре за титул первооткрывателя. И действительно, заслуги этого выдающегося ученого неоспоримы. После четырех лет колебаний и сомнений Леметр все же перенимает идею Фридмана о рождении Вселенной из сингулярности и в 1934 г. пытается придать ей физический смысл, говоря о «взрыве изначального атома», впоследствии иронически окрещенного Ф. Хойлем как “Big Bang” (буквально «Большой взрыв»).

Кроме того, несмотря на авторитет Эйнштейна, Леметр до конца своей жизни последовательно защищал необходимость космологической постоянной для общей теории относительности, придавая ей пока не вполне ясный статус «темной энергии» или «энергии вакуума».
Однако в своей первой статье Леметр фактически упустил из поля зрения вариант развития Вселенной по сценарию Большого взрыва. Переоткрыв уравнения Фридмана, он тем не менее не рассмотрел все классы их возможных решений, сфокусировавшись лишь на одном из них, на предельном варианте мира М2 с конечным начальным радиусом Вселенной и бесконечно долгим расширением до нынешнего радиуса. Но даже и это решение он получил, предполагая, что космологическая постоянная имеет некоторое критическое значение, зависящее от плотности вещества во Вселенной.
Потому вызывает недоумение, что историки науки Гарри Нуссбаумер и Лидия Бьери недавно сделали вывод, что «Леметр ничем не обязан Фридману» (Nussbaumer & Bieri, 2009, с. 111). И действительно, «ничем», кроме как пониманием того, что космологическая постоянная – это независимый параметр, и что Вселенная родилась из сингулярности!
По иронии судьбы теория Большого взрыва вскоре после ее признания Эйнштейном оказалась пасынком в научном мире из-за неточности ранних попыток определить значение постоянной Хаббла. В несколько раз занизив оценки расстояний до удаленных галактик, Хаббл получил и соответственно меньший возраст Вселенной. Даже Эйнштейн в свои последние годы жизни отчаялся найти выход из этого парадокса: по геологическим данным возраст Земли оценивался в 4 млрд лет, а по космологическим данным возраст самой Вселенной не превышал 1,7 млрд лет.
 И лишь в 1950-е гг., уже после смерти Хаббла и Эйнштейна, астрономы Вальтер Бааде и Аллан Сандаж из обсерватории Паломар (Южная Калифорния, США) заново обработав результаты наблюдений Хаббла, понизили оценку постоянной Хаббла в восемь раз и во столько же раз повысили возраст Вселенной. Теория Большого взрыва опять стала фаворитом в научном мире.
И лишь в 1950-е гг., уже после смерти Хаббла и Эйнштейна, астрономы Вальтер Бааде и Аллан Сандаж из обсерватории Паломар (Южная Калифорния, США) заново обработав результаты наблюдений Хаббла, понизили оценку постоянной Хаббла в восемь раз и во столько же раз повысили возраст Вселенной. Теория Большого взрыва опять стала фаворитом в научном мире.
Добавим, что и вклад самого Хаббла в эмпирическую проверку теории расширяющейся Вселенной сейчас подвергается переоценке со стороны астрономов – в пользу Слайфера.
Историки Хелге Краг и Роберт Смит (Kragh, Smith 2008) представляют Фридмана чистым математиком, не придававшем большого значения физическому смыслу своих открытий. Но эта точка зрения опровергается хотя бы его значительными достижениями в аэродинамике и метеорологии. Сборник его избранных трудов 1966 г. и широкий круг проблем, которые он там решает, не оставляет сомнений, что Фридман всегда искал физическое подтверждение своим теориям. Только его преждевременная смерть в возрасте 37 лет не дала ему возможности быть первым, кто связал воедино космологическую теорию и эмпирические данные, и способствовала последующей недооценке его вклада в современную космологию.
По воспоминаниям Екатерины Фридман, ее муж любил цитировать строку из Данте: «Воды, в которые я вступаю, не пересекал еще никто». И действительно, как философ космологии Фридман на голову выше всех остальных участников дебатов 1920-х гг., включая Эйнштейна. Известно, что в конце жизни Эйнштейн называл космологическую постоянную «своей величайшей ошибкой», имея в виду тот факт, что согласно Фридману теория расширяющейся Вселенной могла бы в принципе обойтись и без нее.
В советской литературе теория Большого взрыва долгое время величалась не иначе как «реакционной теорией Леметра». В таких условиях советским физикам было просто опасно отстаивать приоритет Фридмана: они стали открыто выступать в защиту достижений Фридмана только после смерти Сталина. Это изменило отношение к его достижениям и со стороны западных ученых, и с 1970-х гг. в учебниках по космологии уравнения и метрику Фридмана стали называть его именем.
Самый горячий сторонник Фридмана физик-теоретик Я. Зельдович подчеркивает, насколько трудным было то время, когда Фридман совершал свои открытия: «Работы Фридмана опубликованы в 1922—1924 гг., в период больших трудностей. «Россия во мгле» – вот впечатление Герберта Уэллса о Москве и Петрограде 1921 г. В том же номере [немецкого] журнала, где опубликована работа Фридмана [1922 г.], помещено обращение к немецким ученым: собрать научную литературу для русских коллег, которые были отрезаны от нее во время войны и революции. В этих условиях создание теории огромного значения было подвигом не только научным, но и общечеловеческим».
* К сожалению, Эйнштейн приписал это достижение единолично Э. Хабблу, хотя реально оно принадлежит, как минимум, нескольким ученым, главным образом В. Слайферу.
Литература
Фридман А. А. Избранные Труды / Серия «Классики Науки» / АН СССР, 1966.
The Accelerating Universe (Scientific Background on the Nobel Prize in Physics 2011) / Class for Physics of the Royal Swedish Academy of Sciences.
Belenkiy A. Alexander Friedmann and the origins of modern cosmology // Physics Today. 2012. № 65(10). P. 38—43.
Einstein A. The Meaning of Relativity. Princeton University Press. Third edition with an appendix (1946), Fourth edition with further appendix (1950), Fifth edition (1951), Six Edition (2004).
Eddington A. S. The Mathematical Theory of Relativity. London: Cambridge U. Press, 1923.
Kragh H., Smith R. W. Who discovered the expanding universe? // History of Science. 2003. № 41. P. 141—162.
Livio M. Lost in translation: Mystery of the missing text solved // Nature. 2011. № 479. P. 171—173.
Nussbaumer H., Bieri L. Discovering the Expanding Universe. CUP, 2009.
Perlmutter S. Supernovae, Dark Energy, and the Accelerating Universe // Physics Today. 2003. № 56(4). P. 53—60.
Tropp E. A. et al. Alexander A. Friedmann: The Man Who Made the Universe Expand. Cambridge University Press, 1993, 2006.
Тропп Э.А. и др. Александр Александрович Фридман. Жизнь и деятельность. Киев: КомКнига, 2006. 304 с.
Автор выражает признательность Алексею Кожевникову (Alexei Kojevnikov, UBC) за обсуждения истории вопроса, Карло Бинакеру (Carlo Beenakker, Leiden University) из университета Лейдена за публикацию писем Фридмана Эренфесту, Сабине Лер (Sabine Lehr, Springer DE) из издательства Шпрингер за точные даты публикаций Фридмана и Эйнштейна, Галине Житлиной (Richmond BC) за помощь в подготовке текста к публикации
Редакция благодарят за помощь в оперативном получении фотографий и прав на их публикацию Лилиан Моэн (Liliane Moens) (Архивы Джорджа Леметра, Католический университет Лувена, Центр исследований Земли и климата Дж. Леметра, Лувен-ля-Нёв, Бельгия); Карло Бинаккера (Carlo Beenakker) (Институт Лоренца, Лейденский университет, Лейден, Нидерланды), Лорен Амундсон (Lauren Amundson) (Архив Обсерватории Лоуэлла, Флагстафф, Аризона, США), В. М. Катцова и Е. Л. Махоткину (Главная геофизическая обсерватория им. А. И. Воейкова, Санкт-Петербург)











