: 22 июл 2013 , «Но чтоб сие здание [Академия] непременно и полезно было, то имеет оное само себя править» , том 50,
№2
Как создается инженерное наукоемкое ПО мирового класса
Всего несколько десятилетий назад рутинные расчеты и оформление технической документации занимали основную часть рабочего времени инженера. Все изменилось после появления систем автоматизированного проектирования (САПР). Сегодня САПР и инженерное программное обеспечение (ПО) – это важнейшая для промышленности отрасль, общий объем которой составляет более 10 млрд долл. в год. С момента своего рождения и на протяжении уже пятидесяти лет эта индустрия является интенсивным потребителем научных исследований и разработок. Предметная область, включающая в себя задачи вычислительной математики, математического моделирования, оптимизации, исследования операций и других дисциплин, постоянно требует усовершенствования известных подходов и разработки новых методов и алгоритмов. Одним из таких направлений стало геометрическое моделирование. Использование геометрических моделей позволяет решить широчайший спектр производственных задач, давая такие преимущества, как сокращение затрат на проектирование, возможность оперативно вносить изменения в конструкцию изделия, удешевление производства, сокращение сроков вывода нового продукта на рынок
В сознании большинства людей разработка программного обеспечения в первую очередь связана с веб-дизайном, интернет-поиском, документооборотом или компьютерными играми. Мы ежедневно пользуемся подобными приложениями на работе и дома, а названия корпораций Microsoft, Google, Facebook и Apple сможет написать без ошибок даже первоклассник.
В то же время индустрия разработки ПО, которая за полувековую историю своего существования самым решающим образом повлияла на наше окружение – от дизайна электрического чайника или мебели до архитектуры домов и проектирования самолетов, по-прежнему остается малоизвестной широкой аудитории. Речь идет об инженерном ПО: автоматизированном проектировании (Computer-Aided Design, CAD, или САПР), производстве (Computer-Aided Manufacturing, CAM), средствах инженерного анализа (Computer-Aided Engineering, CAE) и управлении жизненным циклом изделия (Product Lifecycle Management, PLM), являющихся неотъемлемыми инструментами повседневной работы современного инженера.
Важными особенностями инженерного ПО являются высокая степень наукоемости и глубокое сопряжение фундаментальных математических и инженерных дисциплин непосредственно с промышленным производством. Это стало одной из причин появления нового научного направления – геометрического моделирования. С одной стороны, оно тесно переплетается с математическим моделированием, вычислительной математикой, дифференциальной геометрией и алгоритмами работы над структурами данных, с другой – в задачах геометрического моделирования присутствует гораздо больше индустриальной прагматики. Здесь, в отличие от научного подхода, требуется не просто реализовать программный прототип, подходящий для решения частной задачи и интересный ограниченному кругу пользователей, но и создать работоспособное, надежное и удобное ПО, которое станет инструментом повседневной деятельности для миллионов инженеров с самым широким спектром задач промышленного производства.
На пути к российскому ядру
Фундаментом всех современных CAD, позволяющих работать с трехмерной цифровой моделью изделия, является программная компонента, называемая ядром трехмерного геометрического моделирования. Основные функции ядра включают в себя средства топологического представления трехмерной модели сплошного тела в виде специальных структур данных (таких как B-Rep, Boundary Representation, граничное представление), операции создания тел произвольной формы (например, вытягивание двумерного контура вдоль заданной траектории или булевы операции над двумя телами) и средства диагностики модели (расчет массово-инерционных характеристик, определение столкновений и др.). Общее же количество функций ядра может достигать нескольких сотен.
История развития отрасли показывает, что разработка промышленного ядра геометрического моделирования – это одна из самых трудных задач при создании инженерного программного обеспечения. Сегодня на мировом рынке известны лишь несколько поставщиков промышленных геометрических ядер (в основном речь идет о двух конкурентах – ACIS и Parasolid, имеющих одни и те же научные корни в британском Кембридже), от которых коммерчески и технологически зависит огромная часть рынка САПР и смежных продуктов. Эти программные компоненты начали создаваться с середины 1980-х гг., и к настоящему моменту общая трудоемкость их разработки составила несколько сотен человеко-лет.
Наряду с такими достоинствами, как высокая степень отлаженности и апробированности на миллионах конечно-пользовательских сценариев, существующим геометрическим ядрам присущи и некоторые ограничения, связанные прежде всего с тем, что программная архитектура ядер была спроектирована давно и во многом не отвечает современным потребностям. К одной из проблем, в частности, относится поддержка многопроцессорных и многоядерных аппаратных платформ.
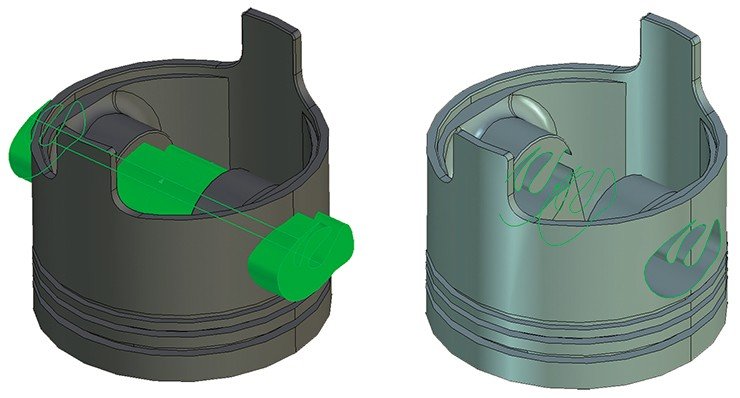
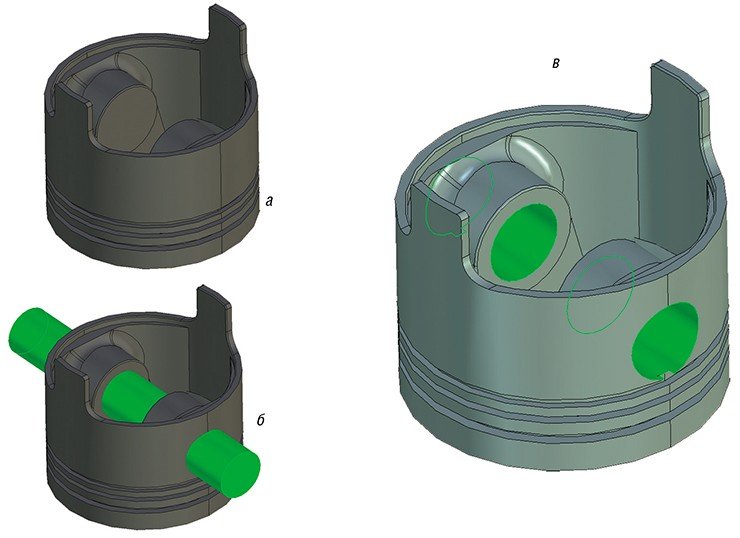
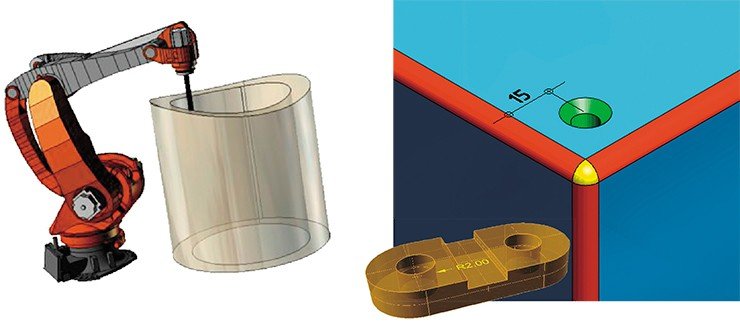
В заготовке детали необходимо проделать пару отверстий, для этого с помощью двумерного профиля (окружность или сплайн по точкам) создается тело «выталкивания» (соответственно цилиндр или NURBS-поверхность), которое позиционируется в пространстве и затем применяется булева операция вычитания. Фактически эта операция является аналогом сверления или другого способа удаления материала
Исходя из необходимости решать перечисленные задачи и вместе с тем учитывая потребность развивать отечественную технологическую базу, Министерство промышленности и торговли РФ в 2011 г. инициировало трехлетний НИОКР-проект по созданию собственного ядра геометрического моделирования («Российское геометрическое ядро»). Над проектом работает комплексный коллектив ведущих российских групп разработчиков под руководством Московского государственного технологического университета СТАНКИН. В область ответственности компании ЛЕДАС входит разработка ключевого модуля и алгоритмов ядра для решения задачи конструирования пересечения кривых, поверхностей и топологических структур.
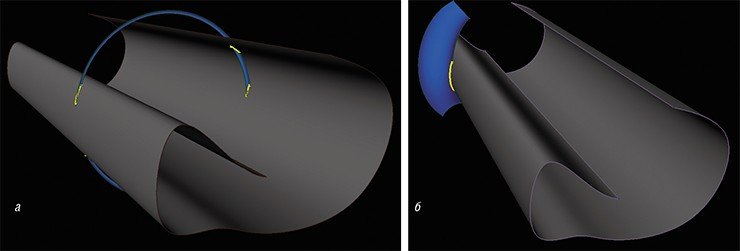
Однако при ближайшем рассмотрении выясняются более серьезные моменты, требующие не только общих знаний методов решения систем линейных и нелинейных уравнений, теории интерполяции, обыкновенных дифференциальных уравнений и алгоритмов вычислительной геометрии, но и ряда специальных подходов, интенсивно развивавшихся последние 20 лет
Однако разработка и реализация современных методов, выполненная на хорошем научно-техническом уровне, является лишь самым начальным этапом создания работоспособного ПО. Первая версия реализованного алгоритма неизбежно не будет учитывать сотни специфических случаев, о которых редко упоминают в технических публикациях, но они невероятно часто встречаются в инженерной практике. К ним можно отнести разнообразные случаи частичного касания, пересечения или прилегания ребер или граней тела, проблему точностей или специальную обработку канонических поверхностей (плоскостей, цилиндров, сфер, торов). Конечно, речь идет не об обычных ошибках кодирования или так называемых багах ПО, а о том, что не существует универсального метода, пригодного для применения во всех случаях. Поэтому реализацию алгоритмов необходимо отлаживать и «полировать» на тысячах индустриальных сценариев, взятых из реального производства.
Геометрический решатель – «великий комбинатор»
Другой важной компонентой САПР является геометрический решатель ограничений. Компания ЛЕДАС с 2002 г. разрабатывала продукты LGS 2D и LGS 3D (LEDAS Geometric Solver) и успешно вывела их на международный рынок, который с начала 1990-х гг. был по сути монополизирован британской компанией D-Cubed (сейчас – подразделение Siemens PLM Software). Эти решатели были лицензированы десятками компаний-производителей САПР из России, США, Японии, Италии, Германии, Южной Кореи, Израиля, Китая и других стран.
Параллельно с работой над собственным продуктом специалисты ЛЕДАС в течение многих лет занимались разработкой аналогичной программной компоненты по специальному заказу Dassault Systemes. Эта компонента была встроена в продукты CATIA, и в ее составе ¬используется инженерами на сотнях тысяч рабочих мест по всему миру, в том числе в корпорациях Toyota, Honda, Airbus, Boeing и др. Чтобы проиллюстрировать, почему так важен геометрический решатель ограничений, рассмотрим несколько задач проектирования.
Можно назвать две причины, по которым компания ЛЕДАС смогла за относительно короткое время занять заметное место на мировом рынке САПР в нише разработки высокотехнологических математических компонент. Во-первых, это общая технологическая и математическая культура сотрудников. В новосибирском Академгородке, где была основана и продолжает работать компания, существуют сильные научные школы в области программирования, вычислительной математики, кибернетики и оптимизации, связанные с именами А. П. Ершова, А. А. Ляпунова, Л. В. Канторовича, Н. Н. Яненко и др. Во-вторых, продвижению на мировой рынок способствовало многолетнее сотрудничество ЛЕДАС с французской корпорацией Dassault Systemes. Начав работать над совместным проектом по внедрению в CATIA технологии недоопределенных вычислений для решения широкого класса задач проектирования, специалисты ЛЕДАСа сумели точнее понять проблематику актуальных задач САПР.
На сегодняшний день портфолио компании состоит из десятков успешных проектов, выполненных по заказу ведущих мировых поставщиков CAD и CAM и нескольких собственных продуктов, успешно выведенных на мировой рынок. О некоторых из них – от создания и управления цифровой моделью изделия до вопросов производства ее физического экземпляра – рассказывают авторы статьи
Слово «design» в переводе на русский язык имеет как минимум два значения: графический дизайн и проектирование. При этом если дизайнер часто предпочитает рисовать исходный эскиз от руки, то инженеру требуется построение точных форм с заранее заданными соотношениями и свойствами.
Типичная задача инженера-конструктора – сборка трехмерной модели механизма, состоящей из деталей, точно позиционированных по отношению друг к другу. Позиционирование происходит с помощью таких геометрических ограничений, как параллельность, расстояние, угол, касание, концентричность и др. Чтобы собрать механизм, необходимо решить систему из таких ограничений. Это и является функцией специальной программной компоненты – геометрического решателя. Имея заданную систему ограничений, геометрический решатель генерирует систему нелинейных алгебраических и тригонометрических уравнений, находит допустимое решение и в качестве ответа применяет пространственные трансформации к каждой детали в сборке. В итоге детали оказываются в таком положении, при котором все принятые ограничения удовлетворены.
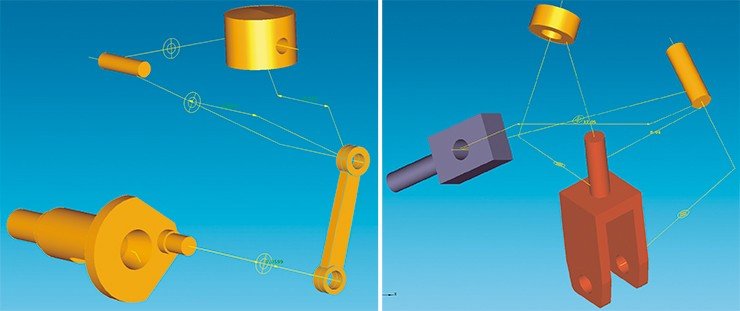
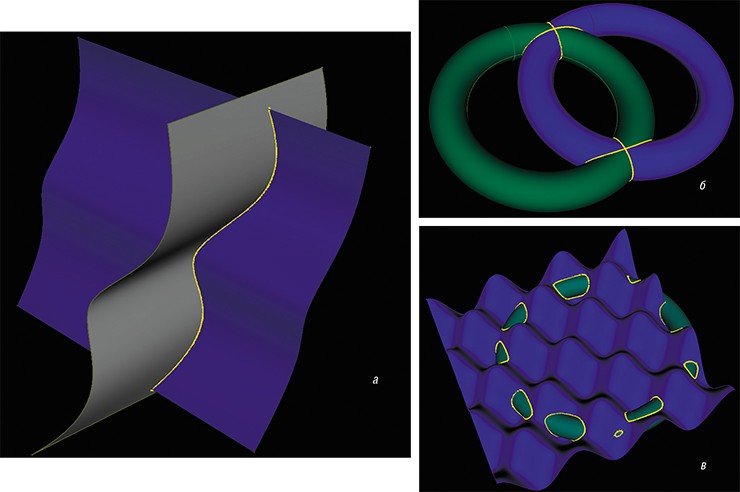
Несмотря на то что решение нелинейных систем – это хорошо известная задача вычислительной математики, практика показывает, что системы уравнений, получающиеся из геометрических ограничений в САПР, весьма специфичны. Они могут быть недоопределенными, переопределенными и разреженными. Чаще всего ¬системы -уравнений недоопределены. Каждая твердотельная трехмерная деталь имеет шесть степеней свободы: три трансляционных и три ротационных. Инженер с помощью ограничений фиксирует только часть степеней свободы механизма (чтобы в нем остались определенные кинематические сочленения), а система уравнений для его расчета оказывается недоопределенной. Из бесконечного множества возможных решений геометрический решатель должен выбрать тот, при котором положение деталей максимально приближено к начальному (эскизному).
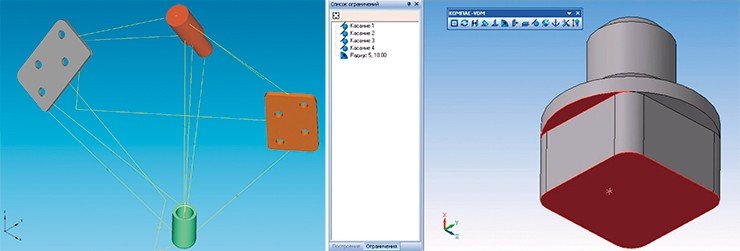
С другой стороны, система уравнений может быть и переопределенной. Например, если взять простую модель – дощатый дом – и задать естественные ограничения параллельности и перпендикулярности для всех пар досок, то возникнет переопределенность, поскольку из одних параллельностей и перпендикулярностей следуют другие. На практике это означает, что в системе уравнений будут линейные зависимости, которые могут привести к серьезной проблеме. Если в исходной модели присутствуют неточности входных данных или накапливается погрешность машинных вычислений, то зависимости между отдельными уравнениями системы становятся близкими к линейным, хотя, строго говоря, таковыми не являются. Это порождает резкий рост числа обусловленности системы уравнений, вычисления становятся неустойчивыми, свойство сходимости к решению теряется.
Третьей особенностью является разреженность систем ограничений. Как правило, каждое ограничение связывает всего два объекта, например, задает концентричность двух цилиндров. Это означает, что система нелинейных уравнений представляет собой набор слабо связанных друг с другом подсистем, что открывает путь к специальным методам декомпозиции, сформулированным как в алгебраической, так и в геометрической постановке.
Автоматизация листового раскроя: пилите, Шура, пилите
Итак, цифровая модель изделия спроектирована, и пришло время производства физического экземпляра. Появившиеся в последнее время технологии 3D-печати (Бэкстрем, 2012]), вполне пригодные для изготовления макетов или прототипов изделий, пока еще не созрели для серийного производства деталей. Реальных альтернатив станкам с ЧПУ (с числовым программным управлением – NC, numerical control) на горизонте пока не видно.
К настоящему моменту станки с ЧПУ и CAM-системы решили две задачи производства. Во-первых, избавили оператора от необходимости пошагового управления инструментом станка. Вместо этого генерируется программа, записанная в виде так называемого G-кода – списка низкоуровневых управляющих команд, определяющих перемещение головки на определенную позицию или включение/выключение инструмента. Во-вторых, позволили инженеру работать непосредственно с цифровой моделью и чертежом в графическом представлении. Инженер указывает последовательность применяемых инструментов и траекторию их движения, после чего G-код генерируется CAM-системой автоматически.
Сегодня основной фокус исследований и разработок в CAM сместился на высокоуровневую автоматизацию, которая позволяет практически исключить инженера CAM из цепочки. Менеджер формирует номенклатуру заказа (чертежи и модели деталей, их материал и количество) и определяет ресурсы (тип станка, имеющиеся инструменты). Далее продвинутая CAM-система, используя «зашитые» в нее интеллектуальные алгоритмы, самостоятельно выбирает способ и последовательность обработки деталей.
Примером вычислительно сложной CAM-задачи, которой по заказу одного из ведущих мировых CAM-поставщиков в течение нескольких последних лет занимаются специалисты компании ЛЕДАС, является автоматизация раскроя листового материала (металла или разнообразных композитов). В этом случае необходимо решить две задачи: во-первых, автоматически и оптимально (с минимальным расходом материала) разместить детали на листах; во-вторых, определить набор требуемых инструментов, оптимальную последовательность их применения и траекторию движения.
Первая задача хорошо известна специалистам по дискретной оптимизации как задача оптимального раскроя (cutting problem), или задача упаковки (packing problem). Даже в простейшей одномерной постановке она является NP-трудной. Другими словами, невозможно получить оптимальное решение за приемлемое время. Если же говорить о реальном промышленном производстве, то оно имеет дело с существенно более сложной задачей – размещением на листе двумерных деталей произвольной формы. В этом случае для получения какого-либо квазиоптимального решения требуется привлечение широкого спектра методов вычислительной геометрии, оптимизации и исследования операций – от построения разности Минковского до алгоритмов поиска типа имитации отжига.
Вторая задача – расчет оптимальной последовательности обработки деталей – подразумевает необходимость учитывать большой набор трудноформализуемых технологических ограничений. Например, при простейшей лазерной резке необходимо специальным образом позиционировать точки включения лазера (на определенном расстоянии от контура детали), поскольку в этих точках лазер оставляет «наплывы».
Наибольшее количество технологических ограничений требуется учитывать при генерации последовательности действий координатно-пробивных и вырубных станков (punching machine). Технология заключается в вырубании материала вокруг деталей отдельными ударами. Здесь необходимо учитывать необходимость перекрывания отпечатков соседних ударов (чтобы не появлялись заусеницы из-за неточности позиционирования), не допускать неконтролируемого выпадения металла, просчитывать возможные изгибы или провисания тяжелого листа, различные способы извлечения крупных деталей (например, с помощью индустриального робота) и десятки других требований. Также большое значение имеет количество смен инструментов и минимизация длины траектории движения.
История инженерного ПО помнит не одну технологическую революцию и сопутствующие взлеты и падения небольших стартапов и крупных корпораций. Сегодня, как и тридцать лет назад, индустрию нельзя назвать стагнирующей. Далеко не все проблемы решены, происходит открытие и освоение новых рынков. Потребность в инновациях и творческом подходе по-прежнему очень высока – как на уровне создания новых фундаментальных алгоритмов и методов, так и на уровне реализации работающих и отлаженных технологий и программных систем, учитывающих требования промышленного производства.
Не погружаясь глубоко в детали описания задач геометрического моделирования, инженерного анализа или управления данными об изделии, перечислим несколько актуальных направлений развития отрасли.
Во-первых, это поддержка современных многопроцессорных и многоядерных аппаратных платформ. Для этого необходимо разрабатывать специальные масштабируемые параллельные алгоритмы. Во-вторых, это технология запуска САПР в «облаке» (cloud computing), когда программное обеспечение доступно через веб-браузер или с помощью средств виртуализации. Особенно заманчиво здесь выглядит возможность управления «тяжелым» ресурсоемким САПР-приложением с любого смартфона. В-третьих, серьезной проблемой является трансляция трехмерной модели между разными форматами данных и САПР-платформами, поставляемыми конкурирующими производителями ПО. И, наконец, максимальная интеллектуализация и автоматизация производственных процессов, которая позволит инженеру сфокусироваться на новых идеях, а не на деталях их реализации.
Список может быть легко продолжен десятками других специализированных задач, к которым относится проблема поиска трехмерных моделей в неструктурированном хранилище данных, исследование новых типов пользовательских интерфейсов, вопрос использования САПР совместно с 3D-принтерами и сканерами и многие другие.
Приятно отметить, что за последние несколько лет российские компании-разработчики, набравшись опыта в ходе тесного взаимодействия с ведущими мировыми поставщиками или во время продвижения собственных конечно-пользовательских программных продуктов на российском рынке, становятся все более конкурентоспособными на мировой арене как в технологическом, так и в маркетинговом плане. Нет сомнений, что в ближайшие несколько лет инженерное ПО отечественного производства сможет достичь заметного присутствия на глобальном, уверенно растущем рынке системы автоматизированного проектирования .
Литература
Баранов Л., Козлов С., Сёмин Д., Снытников Н. Российское 3D-ядро: архитектура и приложения // http://isicad.ru/ru/articles.php?article_num=16129.
Бернар Ф. DASSAULT SYSTEMES: история успеха // http://isicad.ru/ru/articles.php?article_num=14122.
Бэкстрем М., Реннар Л.-Э., Коптюг А. В. Запчасти для скелета // Наука из первых рук. 2012. № 2 (44). С. 45—57.
Волков Ю. С., Мирошниченко В. Л., Фадеев С. И. Сплайны как инструмент геометрического моделирования (к 80-летию со дня рождения Ю. С. Завьялова) // Сиб. электрон. матем. изв. 2011 № 8. A.11-A.16.
Ершов А. Алгоритмы и программные системы для геометрических задач параметрического проектирования // Дис. канд. физ.-мат. наук. Новосибирск, 2007.
Ушаков Д. На ядре // http://isicad.ru/ru/articles.php?article_num=14210.
Ушаков Д. NURBS и САПР: 30 лет вместе // http://isicad.ru/ru/articles.php?article_num=14924.
Ушаков Д. Вариационное прямое моделирование, или как сохранить намерения проектировщика в САПР без истории построения // http://isicad.ru/ru/articles.php?article_num=12711.
Ярес Э. Русские САПРы // http://isicad.ru/ru/articles.php?article_num=1605368.
Coons S. A. An outline of the requirements for a computer-aided design system // Proceedings of the AFIPS ‘63 (Spring), May 21-23, (1963) 299-304.
David E. Weisberg. The Engineering Design Revolution // http://www.cadhistory.net/.
: 22 июл 2013 , «Но чтоб сие здание [Академия] непременно и полезно было, то имеет оное само себя править» , том 50,
№2 
