Михаил Алексеевич Лаврентьев: «Нет ученых без учеников».
К основанию пространственных квазиконформных отображений
Автор этой статьи, в настоящее время профессор Университета Оклахомы (США), сформировался как математик в рамках сибирской школы геометрической теории функций, возникшей на основе работ М.А. Лаврентьева, П.П. Белинского и Ю.Г. Решетняка. В этом выпуске, посвященном 115-летнему юбилею М. А. Лаврентьева, он, рассказывая о неожиданном результате, полученном им в геометрической теории функций, отмечает, что этот результат – еще одно подтверждение известного свойства М.А. Лаврентьева высказывать гипотезы в отношении важнейших направлений науки, благодаря которым эти направления получали новое, зачастую неожиданное развитие. В свое время так случилось и с теорией пространственных квазиконформных отображений, основанной М.А. Лаврентьевым в 30-х годах в связи с потребностями в приложениях для пространственных течений сжимаемой среды
Так уж получилось, что с осени 1990 г., в дополнение к моей работе в Институте математики СО АН, начавшейся после окончания НГУ в 1973 г, я стал полным профессором математики на Западе – сначала один год в Автономном университете Барселоны, а потом в Университете Оклахомы (США), где и работаю до сих пор (уйдя год назад из ИМ).
Приехав прошлым летом в Петербург на конференцию по квантовой топологии и встретившись потом в Хельсинки с финскими коллегами, я с удивлением понял, что у меня получается весьма неожиданный результат в области, из которой я вырос как геометр и тополог – в теории пространственных отображений с ограниченным искажением или, как их сейчас называют, квазирегулярных отображений, основанной в 30-х гг. прошлого столетия Михаилом Алексеевичем Лаврентьевым.
И поэтому, когда наш разговор с моим старым другом из Академгородка свернул на тему готовящегося выпуска журнала к большому юбилею – 115-летию со дня рождения ставшего легендой еще при жизни, выдающегося математика и механика М.А. Лаврентьева, я согласился написать эту короткую заметку, целью которой не является какое-то «глобальное размышление» о М.А. Лаврентьеве – даже и в математике. Слишком ко многому он имел непосредственное отношение, и я боюсь, что чего-то, к сожалению, я просто не знаю.
До сих пор живы его принципы и научные школы, заложенные им более 50 лет назад, в том числе, и легший в основу«сибирской» академической науки знаменитый «треугольник Лаврентьева», объединяющий науку, образование и внедрение научных результатов в практику, и его любимая фраза: «Нет ученых без учеников».
С другой стороны, его единомышленником в математике был Павел Петрович Белинский, бывший его ученик, декан математического факультета НГУ и заведующий отделом теории функций Института математики СО РАН, чьи работы были очень близки к математическим интересам Лаврентьева. Они вместе писали статьи, публиковавшиеся в том числе в престижных зарубежных изданиях. П. П. Белинский был первым математиком из Академгородка, поехавшим в 1968 г. в длительную поездку по Америке. В каком-то смысле аналогичную роль Павел Петрович сыграл и в моем становлении математиком с хорошей геометрической интуицией, несмотря на то, что моим непосредственным руководителем был С. Л. Крушкаль, с которым я стал работать с 3-го курса матфака и который сам был учеником Белинского. Я хорошо помню наши длительные дискуссии с Павлом Петровичем, когда я, будучи студентом, объяснял ему многочисленные доказательства моего результата о неожиданной геометрии действия относительно простой дискретной группы в пространстве. Впоследствии эта работа была представлена М. А. Лаврентьевым для публикации в Докладах Академии наук СССР, сделав меня известным среди специалистов в теории клейновых групп в пространстве.

Через эту личную призму моей близости к Павлу Петровичу Белинскому, ученику М. А. Лаврентьева, я думаю, что могу считать М. А. Лаврентьева своим «математическим дедом». И хотел бы надеяться, что это будет отражено в рамках так называемого «Генеалогического Математического Проекта», создаваемого онлайн Американским математическим Обществом, но, к сожалению, российская математика в нем освещена довольно слабо...
Относительно моей новой конструкции в теории квазирегулярных отображений в пространстве, связанной с идеями М.А. Лаврентьева, П.П. Белинского и В.А. Зорича можно писать много, так как она соединяет воедино различные области математики, в которых коллеги считают меня экспертом: дискретные действия групп в 3-х и 4-х мерных пространствах, нетривиальные 4-х мерные кобордизмы (и известную гипотезу С.П. Новикова), геометрические структуры на многообразиях и их пространства Тейхмюллера, и связанные с ними алгебраические многообразия представлений их фундаментальных групп, ну и конечно, теорию пространственных квазиконформных отображений. И что интересно, этот неожиданный результат в геометрической теории функций оказался новым подтверждением известного яркого свойства Михаила Алексеевича чувствовать важнейшие направления в науке и, более того, высказывать гипотезы, которые давали этим направлениям новое неожиданное развитие. Так случилось и с теорией пространственных квазиконформных отображений, основанной им в 1930-х гг. в связи с потребностями в приложениях для пространственных течений сжимаемой среды и отсутствием какого-либо аналитического математического аппарата, сопоставимого с теорией аналитических функций на плоскости. В статье, опубликованной в Математическом сборнике в 1935 г., М.А. Лаврентьев увидел в теории квазиконформных отображений эффективный инструмент для решения задач динамики сплошных.
В этой статье и в работе, вышедшей в 1938 г., М.А. Лаврентьев смог сформулировать несколько утверждений-гипотез, решением которых потом занимались лучшие умы, и которые привели к созданию новых направлений в математике: теории пространственных отображений с ограниченным искажением (квазирегулярных отображений), распределения значений квазирегулярных отображений, теории, относящейся к классической теореме Пикара, и т.д.
В частности, по одной из подтвердившихся гипотез М.А. Лаврентьева, доказанной в 1967 г. В.А. Зоричем из МГУ, локально гомеоморфные квазиконформные (квазирегулярные) отображения в 3-х мерном пространстве должны быть глобальными гомеоморфизмами на все пространство, не имеющими никаких «барьеров». В дополнение к своему доказательству гипотезы М.А. Лаврентьева, В.А. Зорич использовал идеи П.П. Белинского для построения такого отображения в 3-х мерном пространстве, имеющего ветвление вдоль семейства параллельных прямых, проходящих через целочисленные точки решетки на плоскости. Это отображение имело существенную особенность в бесконечности и не принимало значение 0.
Эти гипотезы М.А. Лаврентьева и пример Зорича послужили основой для возникновения весьма богатой теории распределения значений для квазирегулярных отображений (в стиле классической теоремы Пикара). На эту тему написано множество книг (включая монографии Ю.Г. Решетняка и Сеппо Рикмана) и статей в наиболее престижных научных журналах, включая статью, опубликованную в Acta Math. в июле 2015 г. (Drasin Pankka, 2015).
Мой «добавочек» к этой проблеме, о котором я коротко рассказываю в настоящей публикации, смог привязать к этой области отображений в 3-х мерном пространстве совсем далекие от этого понятия: 4-х мерные кобордизмы, пространства Тейхмюллера геометрических структур на многообразиях и соответствующие алгебраические многообразия представлений конечнопорожденных групп (фундаментальных групп соответствующих кобордизмов).
С существенной помощью моих недавних результатов в этих топологическо-геометрическо-алгебраических областях, я смог построить неизвестные до сих пор «топологические барьеры» для таких локально гомеоморфных квазирегулярных отображений в 3-х мерном пространстве, препятствующие их продолжению на все пространство.
Что удивительно, так это то, что такие «существенные особенности» на довольно малом Канторовом подмножестве 2-х мерной сферы (где они плотны) не позволяют непрерывно связать образы такого отображения внутри и снаружи этой сферы. И это несмотря на то, что образы внутреннего шара и дополнения к его замыканию относительно построенного отображения являются дополнительными друг к другу и взаимно зацепленными: их общей границей является «поверхность» бесконечного рода, топологические ручки которой плотны на ней (разбиение Хегора 3-х мерной сферы бесконечного рода). Это локально гомеоморфное квазирегулярное отображение 3-х мерной сферы в себя является отображением, согласованным с конформным действием на сфере равномерной 3-х мерной гиперболической решетки Г (с 2-мерной сферой в качестве предельного множества) и ее гомоморфного образа G, Ф: Г → G, действующего конформно и разрывно на дополнении в 3-х мерной сфере к «поверхности» бесконечного рода и имеющего своим ядром 3-порожденную свободную подгруппу в Г.

К чему привела Интересная Симметрия Теннисного Мячика моей Дочери Эни
Этот теннисный мячик с 4-мя выделенными точками (симметрично разделенными белой петлей) можно продеформировать в объединение 4-х шаров с взаимно ортогональными граничными сферами. При этом выделенные точки будут соответствовать тройкам таких сфер, пересекающимся в этих вершинах. Если теперь натянуть пленку (топологический диск) на нашу белую петлю и покрыть ее конечным множеством других шаров, чьи граничные сферы пересекают друг друга (и первые 4 сферы) либо под прямыми, либо под 60-градусными углами, то дополнение ко всем нашим шарам будет объединением двух «симметричных» непересекающихся полиэдров Р и Р', с попарно равными двугранными углами. Оказывается, что есть комбинаторно подобный выпуклый полиэдр П в 3-х мерном пространстве Лобачевского, которое можно реализовать в единичном шаре В (и в его дополнении В', содержащем такой же полиэдр П', «симметричный» П). Группа Г изометрий пространства Лобачевского, порожденная отражениями в гранях П и П’, оказывается 3-мерной гиперболической решеткой, которая определяет алгебраический гомоморфизм Ф: Г → G на дискретную группу G, конформно действующую в 3-х мерном пространстве (и в ограниченном им 4-х мерном пространстве Лобачевского) и порожденную отражениями в гранях полиэдров П и П'. Это действие определяет так называемый 4-х мерный (нетривиальный) гиперболический кобордизм, чьи «симметричные» граничные компоненты П/G и П'/G накрываются двумя G-инвариантными связными компонентами О и О' множества разрывности О(G) группы G в 3-х мерном пространстве. Вся эта конструкция требует точной геометрической реализации (с указанными свойствами двугранных углов и т.п.). Это можно сделать «детскими кубиками», чьи размеры взаимосвязаны (см. рисунок), и поверхности которых покрыты шарами с нашими условиями на их граничные сферы. Сделав отражения относительно наших первых (взаимно ортогональных) трех сфер, полученных деформацией теннисного мячика, можно увидеть такую конфигурацию этих «детских кубиков»: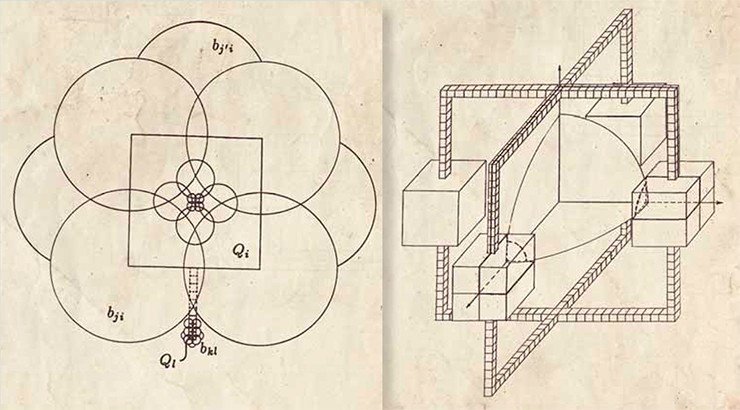
Здесь надо заметить, что наш полиэдр Р находится внутри этой конфигурации, а «симметричный» ему полиэдр Р’ – вне ее. Теперь можно закончить главную идею конструкции нашего 4-кобордизма и квазирегулярного отображения F 3-х мерного пространства в себя, определив это отображение F на полиэдрах П и П’, квазиконфомно отображаемых на полиэдры Р и Р’, и дальше продолжаемое по симметрии до отображения 3-х мерного шара В и его дополнения В’ на взаимно зацепленные области О и О', имеющие общую граничную «поверхность» с плотным на ней множеством топологических «ручек». Построенное квазирегулярное отображение F является локальным (взаимно однозначным) гомеоморфизмом, но не имеет такого глобального свойства. Кроме того, оно имеет «топологический барьер» в виде плотного Канторова подмножества существенных особых точек на граничной сфере шара В, в любую окрестность которых оно непродолжаемо. Эти свойства следуют из того, что наш гомоморфизм Ф: Г → G (3-х мерной гиперболической решетки Г на дискретную группу G) имеет большую ядро-подгруппу К(Ф) в Г, являющуюся свободной группой на 3-х порождающих. Поэтому, когда точка х стремится к граничной сфере шара В вдоль вложения графа Кэли подгруппы К(Ф) (в шаре В или В'), ее образы F(х) бегут вдоль «заполненных зацепленных ручек» области О или О', не имея при этом никакого предела.
Все детали этой конструкции можно найти в моей работе Topological barriers for locally homeomorphic quasiregular mappings in 3-space.
Таким образом, после этого запутанного бега с барьерами, мы возвращаемся к нашей начальной идее, основанной на интересной симметрии обычного желтого теннисного мячика, связывающей воедино такие далекие на первый взгляд области математики. Ко всему этому можно прийти, вспоминая впечатляющие беседы мастистых ученых и их начинающих учеников, как иллюстрацию фразы Михаила Алексеевича Лаврентьева: «Нет ученых без учеников».
Литература
Апанасов Б. Н. Об одном классе Клейновых групп // Доклады АН СССР, 1974 Т. 215.
Белинский П. П., Лаврентьев М. А. Некоторые проблемы геометрической теории функций // Труды математического института Стеклова. М.: Наука, 1972. Т. 128, № 2. С. 34—40.
Зорич В. А. Теорема М. А. Лаврентьева о квазиконформных отображениях пространства // Математический Сборник, 1967. Т. 74, № 3. С. 417—433.
Лаврентьев М. А. О классе непрерывных отображений // Математический Сборник, 1935. № 42. С. 407—424.
Apanasov B. N. Topological barriers for locally homeomorphic quasiregular mappings in 3-space. http://arxiv.org/abs/1510.08951.