Тайна чашки кофе
«Каждый из нас знает, с какой осторожностью нужно переносить сосуды с жидкостью, чтобы не допустить расплескивания», – такими словами начал свой пионерный доклад в 1967 г. специалист НАСА Абрамсон (Abramson, 1967). Действительно, каждый раз, когда мы несем кофе или чай, мы подспудно уделяем этому вопросу особое внимание. Но причем здесь космические исследования? Оказывается, аналогичный вопрос возникает, например, при разработке ракет, и проблема плескания жидкого топлива при разгоне актуальна по сей день
Чашка кофе – так называлась одна из задач Международного турнира юных физиков 2015 г. (IYPT-2015), посвященная проблеме плескания жидкости при ходьбе. Участникам турнира требовалось определить, как зависит вероятность пролить кофе от формы чашки и других условий эксперимента.
Оказалось, что такой вопрос уже исследовался ранее экспериментально и теоретически, с применением численного моделирования (Mayer and Krechetnikov, 2012). При этом было показано, что при обычной ходьбе расплескивание жидкости связано с неравномерностью шага и чаще всего происходит при разгоне. Был получен и неожиданный результат – вероятность пролить кофе будет тем меньше, чем выше установившаяся средняя скорость движения.
Авторы этой работы в 2012 г. получили шуточный аналог Нобелевской премии – так называемую Шнобелевскую премию, которой награждают нестандартные и, на первый взгляд, не слишком востребованные исследования, которые, тем не менее, привлекают внимание широкой общественности и подстегивают интерес людей к науке, медицине и новым технологиям. Несмотря на такой юмористический характер премии, сами исследования, как правило, отличаются высоким экспериментальным и теоретическим уровнем, а неожиданная постановка задачи провоцирует по-новому взглянуть на окружающий нас мир. Кстати сказать, первым ученым, который был удостоен как Шнобелевской, так и Нобелевской премий, является наш бывший соотечественник, а ныне профессор Манчестерского университета физик Андрей Гейм.
В глубоких водах
В нашей работе мы сосредоточились на исследовании резонансного режима, который не изучался ранее. Такой режим реализуется, когда частота шага при ходьбе совпадает с частотой собственных колебаний жидкости в чашке.
Для определения частот колебательных мод плескания были собраны вибростенды, позволяющие раскачивать чашку на подставке в горизонтальном и вертикальном направлениях с помощью вибратора, создающего синусоидальные механические колебания определенной амплитуды и частоты.

В ходе первых экспериментов было установлено, что добавление в воду кофе и сахара в разумных количествах, а также использование воды разной температуры (от комнатной до кипящей) практически не отражалось на полученных результатах. Поэтому в большей части экспериментов использовалась обычная вода комнатной температуры, лишь слегка подкрашенная кофе для увеличения контраста видеозаписи движения поверхности жидкости.
В экспериментах использовались прозрачные цилиндрические чашки различных радиусов. Как выяснилось, частоты мод плескания с увеличением радиуса чашки уменьшаются. Первая, самая низкочастотная мода плескания возбуждается при горизонтальной раскачке; для чашки с самым большим радиусом (R = 39 мм) резонанс возникал на частоте 3,5 Гц. Отметим, что частота обычного шага человека не превышает 2,5 Гц, поэтому такой резонанс достижим лишь при очень частом, «мелком» шаге. Другие моды плескания, возникающие как при горизонтальных, так и при вертикальных возбуждениях, имели заметно большие частоты, но в данной работе мы ограничились изучением только первой моды.
В результате было установлено, что частота первой моды плескания практически не зависит от высоты жидкости h, если h > R/2, но при меньших заполнениях чашки начинает снижаться с уменьшением h. Фактически при этом наблюдается переход от гравитационных волн на «глубокой воде» к гравитационным волнам на «мелкой воде». Дальнейший анализ задачи был ограничен наиболее практичным и привычным всем любителям кофе случаем «глубокой воды».
Маятник в чашке
Исходя из интуитивных соображений размерности, можно предположить, что циклическая частота ω первой колебательной моды плескания глубокой воды будет зависеть от определенных исходных параметров. В нашем случае это радиус чашки R и ускорение свободного падения g, так как здесь мы имеем дело с гравитационными волнами, где роль возвращающей силы играет именно сила тяжести. Аналогичный набор параметров имеет задача о колебании математического маятника, на основе чего мы можем записать выражение для циклической частоты единственным способом, дающим верную размерность с точностью до безразмерного численного коэффициента ε: ω² = ε ∙ (g/R).

Согласно данным литературы (Lamb, 1945), асимптотическое выражение для случая волн на глубокой воде имеет аналогичный функциональный вид. При этом точное значение коэффициента ε составляет 1,841, а экспериментально полученные нами значения оказались равными 1,8 ± 0,1.
Заметим, что плотность жидкости не является существенным параметром задачи о плескании – аналогично тому, как масса груза не входит в выражение для частоты математического маятника. Правда до сих пор мы не учитывали вклад поверхностного натяжения, который должен приводить к увеличению частоты колебаний в связи с дополнительными энергетическими затратами на увеличение площади поверхности жидкости. Такая ситуация будет уже похожа на случай с пружинным маятником, где масса тела (в данном случае – плотность жидкости) играет существенную роль.
Воспользуемся опять методом анализа размерностей физических величин. Отношение характерных изменений энергии поверхностного натяжения и потенциальной энергии жидкости в поле тяжести при колебаниях определяется такими существенными параметрами задачи, как коэффициент поверхностного натяжения σ и плотность жидкости ρ, а также упоминаемые ранее R и g. Исходя из того, что это отношение – величина безразмерная, для его оценки получаем σ/(ρgR²), что близко к точному математическому выражению (Lamb, 1945). Подставив значения параметров, определим,что вклад поверхностного натяжения составляет не более 2 % общей энергии системы. Это очень маленькая поправка, меньше погрешности измерений в наших экспериментах, поэтому ей можно пренебречь.
Шире шаг, кофеман!
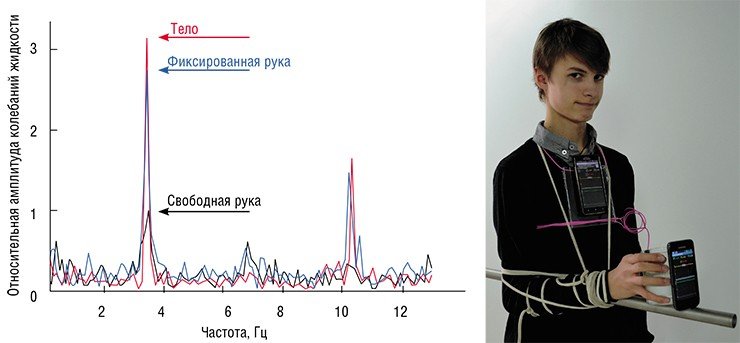
Экспериментальное изучение вопроса о расплескивании жидкости привело к необходимости измерить временную динамику ускорения, сообщаемого ходоком чашке. Так как изучаемый объект при этом перемещался на большие расстояния, потребовался мобильный акселерометр. Его роль прекрасно исполнил обычный смартфон, который дал возможность измерять ускорение в трех пространственных направлениях: вертикальном, продольном и поперечном.
Этот же смартфон использовался и в качестве метронома, который был должен служить ориентиром для задания частоты шага. Уровень подъема жидкости во время ходьбы фиксировался с помощью видеосъемки компактным цифровым фотоаппаратом. Все эти устройства вместе с наполненной чашкой были закреплены на платформе мобильного стенда.
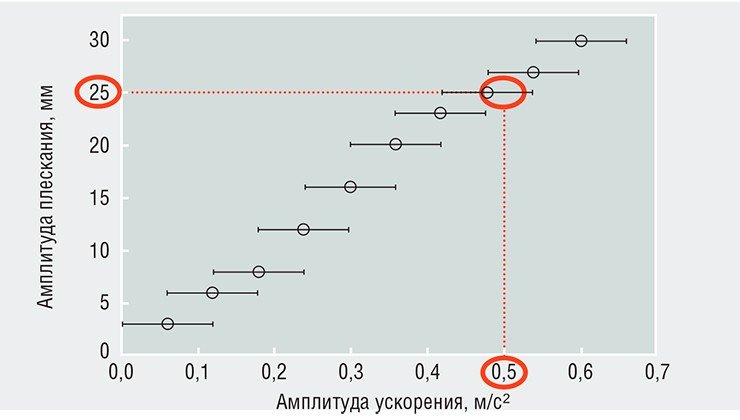
Экспериментальные исследования с помощью мобильного стенда показали, что наибольшая амплитуда плескания жидкости при ходьбе достигается при частоте шага, близкой к собственной частоте первой моды плескания 3,5 Гц. При этой частоте амплитуда плескания составляет 25—30 мм – именно при таком уровне заполнения чашки жидкостью произойдет расплескивание. Конечно, этот экспериментальный ответ справедлив лишь для конкретного ходока. Для получения более общего ответа требуется провести и более широкое исследование, привлекая в качестве ходоков разных людей. Такая работа уже будет затрагивать область биомеханики, нас же больше интересовали физические аспекты вопроса.
Эксперименты показали, что самая большая амплитуда вынужденных колебаний ускорения чашки возникает в продольном направлении, и составляет она около 0,5 м/с². Именно эта проекция ускорения и определяет расплескивание жидкости в чашке.
Амплитуда вертикальной проекции ускорения в два раза меньше; кроме того, как уже упоминалось выше, вертикальные возбуждения способны раскачивать другие колебательные моды, на более высоких частотах, но на данной частоте они находятся «вне игры». Выяснилось также, что в три раза меньшую амплитуду имеют поперечные возбуждения, которые происходят на частоте вдвое меньшей частоты шага. Последнее связано с тем, что цикл колебаний человека (и, естественно, жидкости в чашке) в продольном направлении соответствует одному шагу, а в поперечном – двум последовательным шагам правой и левой ногой.
Для проверки выдвинутой нами гипотезы об определяющей роли продольного возбуждения были проведены дополнительные эксперименты на вибростенде с горизонтальной раскачкой, в которых измерялась зависимость амплитуды плескания жидкости от амплитуды ускорения раскачки. Оказалось, что при амплитуде ускорения 0,5 м/с² амплитуда плескания составляет 25 мм, что находится в хорошем соответствии с данными эксперимента, проведенного при ходьбе с мобильным стендом.
Особое внимание было уделено изучению так называемой демпфирующей (уменьшающей амплитуду колебаний) роли руки. Оказывается, эта конечность может довольно значительно сгладить колебания человеческого тела, возникающие при ходьбе. Чтобы определить, насколько существенно это влияние, мы провели измерения в условиях, когда рука была зафиксирована на туловище специальной шиной. При этом амплитуда вынужденных колебаний возросла почти втрое по сравнению с ситуацией с незакрепленной рукой и сравнялась с амплитудой колебаний тела, которая измерялась еще одним смартфоном, закрепленным на груди самого ходока.
Нас также заинтересовал вопрос, зависит ли исследуемое явление от формы сосуда, так что мы определили моды плескания жидкости при ходьбе в чашках различной формы. Помимо цилиндрических чашек использовалась полусферическая чашка (пиала) и различные конические сосуды.
Оказалось, что в пиале частота колебаний первой моды плескания определяется радиусом полусферы и практически не зависит от глубины наполнения. В конической же чашке глубина наполнения и радиус поверхности жидкости однозначно связаны друг с другом прямой пропорцией, именно эта группа параметров и определяет период собственных колебаний, возникающих в сосуде. К примеру, в конической рюмке с углом при вершине конуса 45° циклическая частота первой моды плескания хорошо описывается выражением ω² = g/r (r – радиус открытой поверхности жидкости), которое аналогично выражению для частоты колебаний математического маятника.
Итак, теоретическое определение собственных частот мод плескания жидкости представляет собой довольно сложную задачу. В этой работе с помощью доступных школьнику математических методов нам удалось получить выражение для собственной частоты низкочастотной моды плескания, которое хорошо согласуется с имеющимися теоретическими данными.
В ходе работ было показано, что, когда частота шага человека, несущего чашку, совпадает с собственной частотой моды плескания, т.е. в случае возникновения резонанса, амплитуда колебаний уровня жидкости максимальна и может составить несколько сантиметров.
Интересным продолжением этого исследования стало бы изучение особенностей биомеханики человеческого тела, определяющих при ходьбе раскачку чашки с жидкостью.
Литература
Abramson H. N. Technical Report N. SP-106, NASA, 1967.
Mayer H. C. and Krechetnikov R. Walking with coffee: Why does it spill? // Phys. Rev. E. 2012. V. 85. Doc. 046117.
Lamb H. Hydrodynamics. Dover, New York, 1945.
Экспериментальные исследования проводились на полигоне в Академпарке (Новосибирск) с использованием измерительного комплекса PASCO
Авторы благодарят команду юных физиков «Школа Пифагора» и сборную российской команды на IYPT‑2015 и их тренеров А. И. Щетникова и А. А. Колчина за конструктивную критику и помощь в подготовке доклада






