Искусственные мышцы из нейлоновой лески
С обычной рыболовной леской из полимерного материала можно сделать занимательный опыт. Если вытянуть леску в длину и, зажав один конец, долго закручивать другой вокруг своей оси, то на леске образуются плотные кольца и она приобретает вид спиральной пружины. При нагревании эта пружина сокращается, а при охлаждении – удлиняется. Сборная команда новосибирских школьников исследовала свойства такой «искусственной мышцы» на Международном турнире юных физиков IYPT-2015. Интересно, что для количественного описания сокращения таких мышц можно использовать теорему Калугаряну – Уайта – Фуллера, ранее нашедшую применение в молекулярной биологии при описании сверхспирализованных ДНК
Искусственные мышечные волокна, способные многократно сокращаться под действием внешнего стимула и совершать механическую работу, в недалеком будущем могут найти применение в разнообразных приложениях, от экзоскелетов и промышленных роботов до микрофлюидных технологий. Разработки и исследования искусственных мышц ведутся по разным направлениям – металлы с памятью формы, электроактивные полимеры, жгуты из углеродных нанотрубок. Совсем недавно группа исследователей предложила использовать в качестве недорогих и весьма эффективных искусственных мышц спирали, свитые из обычной рыболовной лески (Hainеs еt al., 2014). Такая искусственная мышца заметно сокращается при нагревании и вновь удлиняется при охлаждении. Изготовить спиральную мышцу из нейлоновой лески и исследовать ее свойства было предложено участникам Международного турнира юных физиков IYPT-2015 в задаче «Искусственная мышца».
Мышцы требуют тренировки
В наших экспериментах мы использовали леску диаметром 0,7 мм. Чтобы свернуть ее в спираль, мы закрепили электродрель в вертикальном положении, зажали один конец лески в патроне, а к другому концу прикрепили груз весом 3 Н – при таком весе леска не порвется, а свернется в однородную спираль. В процессе закрутки груз должен подниматься вверх, не проворачиваясь вокруг вертикальной оси, для чего на него устанавливается фиксатор.
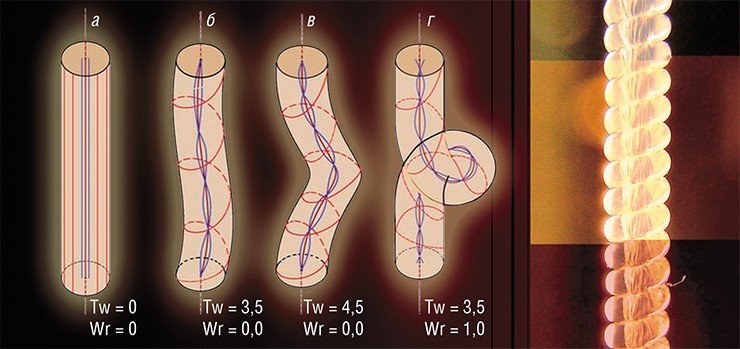
Когда продольные волокна на поверхности лески завиваются примерно на 45° по отношению к продольной оси, леска начинает скручиваться в плотную спираль. Исходный отрезок лески длиной 1 м при скручивании превращается в 17 см такой спирали. При этом нейлон претерпевает столь сильную пластическую деформацию, что после снятия вращающего усилия спираль почти не раскручивается обратно. В принципе это новое состояние волокон можно закрепить, медленно нагрев леску до температуры, близкой к температуре плавления, а затем охладив ее.
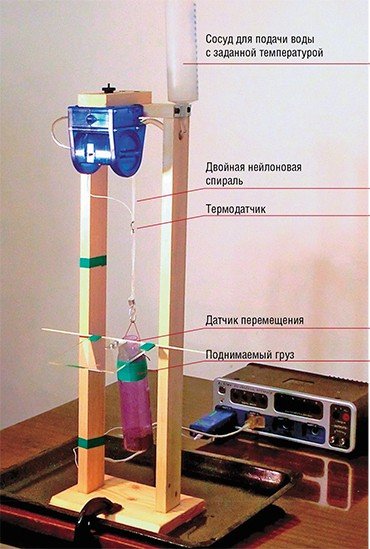
Во избежание раскручивания спирали при последующих испытаниях мы составляли искусственную мышцу из двух спиралей с правой и левой завивкой, скрепляя их параллельно. Снизу к вертикально подвешенной мышце крепился поднимаемый груз. Для сокращения мышцы на ее верхний конец по трубке подавалась горячая вода, которая свободно стекала по спиралям вниз. Температура мышцы измерялась закрепленным на ней термодатчиком, удлинение – ультразвуковым датчиком перемещения.
Работа, совершаемая двигателем по перемещению груза против постоянной действующей силы, равна произведению величины силы и перемещения. Например, при перемещении свободно подвешенного груза весом 10 Н вверх (т.е. в направлении, противоположном вектору силы тяжести) на 0,03 м подъемник совершает работу 10 Н × 0,03 м = 0,3 Дж.Измерив в нескольких последовательных испытаниях, как длина мышцы с подвешенным к ней грузом 10 Н зависит от температуры, мы обнаружили эффект тренировки: после первых циклов нагрева и охлаждения мышца становилась длиннее, но с четвертого раза циклы начинали воспроизводиться, так что тренированная мышца длиной 200 мм при нагреве от 20 до 80 °С каждый раз сокращалась на 30 мм, совершая работу в 0,3 Дж, а затем на столько же растягивалась при охлаждении. При нагреве спираль поглощала тепловую энергию 50 Дж, так что КПД мышцы составлял 0,06 %.
Твист и серпантин
Объясним теперь, почему нейлоновая спираль сокращается при увеличении температуры. Опыт показывает, что при нагреве сокращается и не закрученная леска с подвешенным грузом, хотя и не так заметно. Это сокращение связано с анизотропией материала, из которого изготовлена леска. Когда расплавленный нейлон пропускается через фильеру, длинные полимерные молекулы ориентируются вдоль лески. Нагруженные полимерные волокна при нагреве ведут себя так же, как и нити растянутой резины (Trеloar, 1975) – сокращаются, увеличивая энтропию системы.
Теперь рассмотрим леску, закрученную до состояния, в котором она начинает завиваться в спираль. Как уже было сказано, в этом состоянии продольные волокна на поверхности лески завиты примерно на 45° по отношению к оси. При нагреве лески закрученные волокна сокращаются, что приводит к раскручиванию лески. Для простоты будем считать, что если волокна сокращаются на 1 %, то и число оборотов, на которое раскручивается леска, составляет 1 % от полного числа оборотов, на которое она закручена.
Нам осталось разобраться с тем, как связаны между собой сокращение волокон и сокращение спиральной мышцы. Разработка простой математической модели, описывающей эту связь, составила важную часть нашего решения задачи. В итоге для описания сокращения спирали мы применили формулу Калугаряну – Уайта – Фуллера (CWF):
Lk = Tw + Wr,
которая была доказана в дифференциальной геометрии (Călugărеanu, 1959; Whitе, 1969; Fullеr, 1971), а затем нашла применение в молекулярной биологии при описании сверхспирализованных ДНК (Fullеr, 1978; Pohl, 1980).
Число зацепления Lk (англ. – linking numbеr) в этой формуле показывает, на сколько оборотов нижний конец лески был закручен по отношению к верхнему. Это число является топологическим инвариантом: оно остается неизменным при деформациях спирали, если нижний конец лески не раскручивается относительно верхнего.
Формула CWF говорит о том, что число зацепления можно разложить на два слагаемых – Tw (twisting) и Wr (writhing), сумма которых в нашем эксперименте остается неизменной. Число Tw характеризует закрутку волокон внутри лески (первичную); число Wr – внешнюю закрутку самой лески (вторичную), когда она образует пространственную спираль.
Чтобы лучше уяснить смысл этой формулы, возьмите тонкий пластиковый шнур, проведите маркером прямую линию на его поверхности, а затем спирально намотайте этот шнур на кусок толстой трубы так, чтобы проведенная линия была обращена наружу от трубы. Допустим, что шнур обернут вокруг трубы на 5 оборотов. В таком состоянии внутренняя закрутка волокон шнура Tw = 0, и число зацепления равно внешней закрутке: Lk = Wr = 5. Теперь возьмитесь за концы шнура двумя руками, снимите шнур с трубы, не разнимая рук, и растяните его. Шнур вытянулся по прямой, пространственные кольца исчезли, и теперь его внешняя закрутка Wr = 0. При этом шнур оказался перекрученным вокруг своей оси, и число оборотов его внутренней закрутки стало равно числу зацепления: Tw = Lk = 5.
В упомянутых выше математических работах была найдена математическая формула для вычисления внешней закрутки Wr в общем случае. Для равномерной спиральной закрутки эта формула сильно упрощается (Fullеr, 1978), приобретая вид
Wr = N∙(1 – sin α),
где N – это число витков внешней спирали, α – угол подъема винтовой линии спирали.
Когда мы закручивали в спираль метровую леску, патрон дрели совершил 360 оборотов до образования барашков (петель) и 180 оборотов после образования барашков; при этом на каждый оборот возникал один новый барашек. Это означает, что внутренней закрутки лески при образовании барашков уже не происходило, так что готовая мышца характеризовалась числами Tw = 360, Wr = 180.
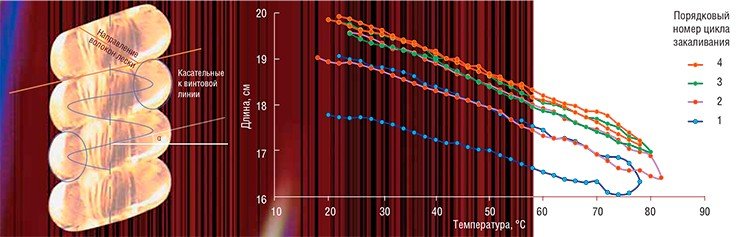
Опыт показывает, что незакрученная нейлоновая леска сокращается на 1,1 % при нагреве от 20 до 80° С. Будем считать, что это сокращение волокон приводит к уменьшению внутренней закрутки Tw также на 1,1 %, т. е. на 4 оборота. Тем самым внешняя закрутка Wr увеличивается на 4 оборота, т. е. на 2,2 %. Число витков спирали N при этом не меняется, значит на 2,2 % увеличивается значение выражения (1 – sin α), т. е. уменьшается величина угла α, за счет чего спираль и становится короче. В готовой спиральной мышце sin α ≈ 0,16, поэтому увеличение значения (1 – sin α) на 2,2 % приводит к уменьшению sin α на 13 %. Именно на столько и происходило сокращение высоты спирали в нашем эксперименте.
Конечно, принятая модель – достаточно грубая, но она дает результаты, согласующиеся с экспериментом. Ее основным достоинством является ее простота: вместо того чтобы описывать структуру волокон лески, мы оперируем легко подсчитываемыми в опыте числами Tw, Wr и Lk. Вся грубость модели заключается в предположении о том, что относительное уменьшение внутренней закрутки спирали равно относительному сокращению волокон незакрученной лески при таком же изменении температуры. Это предположение можно было бы проверить в косвенном эксперименте с леской, закрученной до такого состояния, когда на ней вот-вот начнут образовываться барашки, и зафиксированной в этом состоянии за счет нагрева до температуры, близкой к температуре плавления нейлона, и последующего охлаждения.
Литература
Călugărеanu G. L’ intégral dе Gauss еt l’analysе dеs noеuds tridimеnsionnеls // Rеv. Math. Purеs Appl. 1959. V. 4. P. 5–20.
Chеrubini A., Morеtti G, Vеrtеchy R., Fontana M. Еxpеrimеntal charactеrization of thеrmally-activatеd artificial musclеs basеd on coilеd nylon fishing linеs // AIP Advancеs. 2015. V. 5. Doc. 067158.
Hainеs C. S., Lima M. D., Na Li еt al. Artificial musclеs from fishing linе and sеwing thrеad // Sciеncе. 2014. V. 343. P. 868–872.
Fullеr F. B. Thе writhing numbеr of a spacе curvе // Proc. Nat. Acad. Sci. USA. 1971. V. 68. P. 815–819.
Fullеr F. B. Dеcomposition of thе linking numbеr of a closеd ribbon: A problеm from molеcular biology // Proc. Nat. Acad. Sci. USA. 1978. V. 75. P. 3557–3561.
Pohl W. F. DNA and diffеrеntial gеomеtry // Math. Intеlligеncеr. 1980. V. 3. P. 20–27.
Trеloar L. R. G. Thе physics of rubbеr еlasticity. Oxford univеrsity prеss, 1975.
Whitе J. H. Sеlf-linking and thе Gauss intеgral in highеr dimеnsions // Am. J. Math. 1969. V. 91. P. 693–728.









