Космонавтика

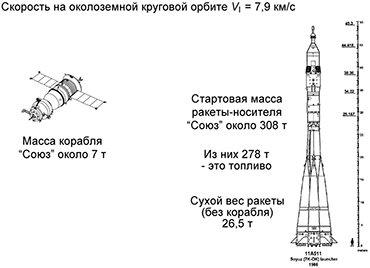Вот космический корабль, на котором летают наши космонавты. Вес его 7 тонн, в нем три человека – и их надо разогнать до скорости 8 км/с. Так вот, чтобы это сделать, приходится строить аппарат для одноразового использования весом более трехсот тонн – и вся эта махина нужна только для того, чтобы маленький космический аппарат вытолкнуть на устойчивую орбиту. Ракета состоит из металлической конструкции и топлива. Их соотношение такое: сухой вес ракеты – 26 тонн, а залитого в нее топлива – почти 280 тонн. Понимаете, на что это похоже? Вы, конечно, пили газировку или пиво из алюминиевых банок. Когда берешь полную банку в руки – она весит четверть килограмма, а когда выпьешь – 6 граммов. Вот почти такое же соотношение веса у заправленной ракеты и пустой. Ощутите, насколько это тонкая машина в инженерном смысле, да и в прямом смысле – тоже!

К антиподам: на спутнике или на лифте?

Есть одна интересная задача, которую я традиционно предлагаю на экзамене. Пусть нам требуется послать груз или пассажиров из одной точки Земли в точку, ей противоположную (т.е. к антиподам, потому что с нашей точки зрения все там ходят вверх ногами, притягиваясь к центру Земли). Как это сделать быстрее?

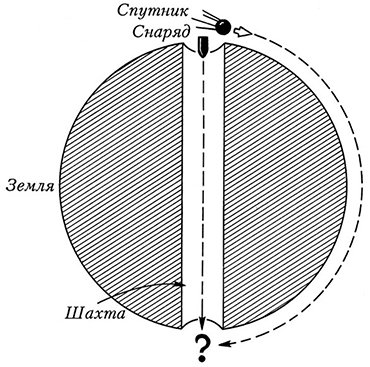Казалось бы, самый быстрый способ – лететь по круговой орбите спутника. С первой космической скоростью спутник облетает Землю за полтора часа, значит, мы можем прилететь к антиподам через 45 минут плюс время на разгон и торможение. Быстрее не получится: если мы добавим спутнику скорости, он пойдет по дальней орбите и лететь будет дольше. К тому же для реализации этого способа потребуется много денег: надо каждый раз сооружать огромную ракету, тратить очень много энергии на запуск.

А вот представьте себе, что мы просверлили Землю насквозь и без начальной скорости просто отпустили снаряд. Он начнет ускоренно падать к центру Земли, затем, набрав скорость, по инерции пролетит через центр и выпрыгнет как раз в антиподальной точке – останется только его вовремя поймать. Такой канал потребуется сделать только один раз, откачать из него воздух, чтобы не замедлял движение, а потом совершенно бесплатно запускать кабину с людьми на ту сторону земного шара и обратно. Вопрос задачи: какое путешествие займет меньше времени – по низкой околоземной орбите искусственного спутника или через центр Земли?

Геостационарная орбита и космический лифт

Среди всех круговых орбит особенно интересна геостационарная орбита, на которой орбитальный период длится столько же, сколько оборот Земли вокруг своей оси, т.е. 23 часа 56 минут и примерно 4 секунды – такова продолжительность звездных суток. Если вы запустили спутник на круговую орбиту, лежащую в экваториальной плоскости Земли на расстоянии примерно 36 тыс. км от земной поверхности (от центра планеты это будет 42 тыс. км), то, обращаясь в плоскости экватора с периодом в одни звездные сутки, он всегда будет висеть над одной и той же точкой земного шара. Таких спутников летают сотни. А зачем они нужны?

Это, например, спутники прямого телевизионного вещания, их специально запустили на геостационарную орбиту, чтобы нам домашнюю антенну в течение суток не крутить туда-сюда. Мы один раз нацеливаем свою спутниковую тарелку на такой спутник и уверены, что он всегда будет в одной и той же точке неба и никуда не денется.

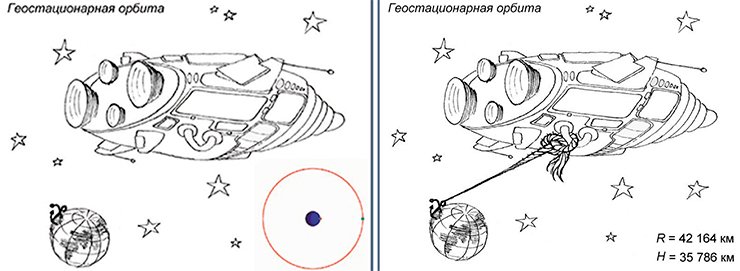
Интересно, что эта особенность геостационарной орбиты открывает нам совершенно фантастические перспективы для космонавтики. С такого спутника можно протянуть на Землю трос, и он не будет наматываться на Землю, потому что спутник относительно земной поверхности не движется. Вдоль этого шнура или каната можно организовать космический лифт. Заметьте: не ракету, которая 98% своей массы выбрасывает, чтобы остальные 2% массы в виде космического корабля отправить в полет, а просто электрический лифт. Прикиньте, сколько в этом случае киловатт-часов электроэнергии потребуется, чтобы подняться в космос, и сколько это будет стоить – считанные копейки получатся.

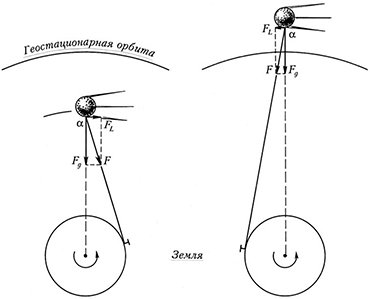Есть, правда, одна неприятная особенность такого спутника: вот запустили мы его на геостационарную орбиту, натянули канатик, но вдруг какая-то случайная небрежность заставила спутник немножко опуститься. Что тогда будет происходить? Спутник оказался ближе к центру Земли, его орбитальный период стал короче, т.е. спутник начнет опережать ту точку поверхности, к которой привязан канатиком, канатик будет наматываться на Землю и тянуть спутник вниз. Тот еще быстрее начнет крутиться – и понятно, что закончится это нехорошо.

Если спутник чуть выше подтолкнуть, тогда он начнет отставать от поверхности Земли – чем больше расстояние, тем меньше скорость обращения и тем больше орбитальный период. Но будет ли это движение устойчивым, не станет ли Земля наматывать канатик в обратную сторону? Это простая механическая задача, которую должен быть способен решить любой физик.

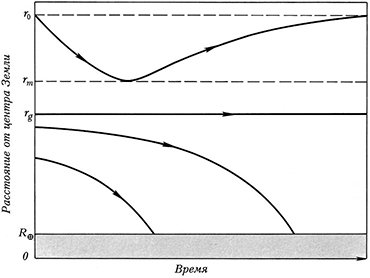Вычисления показывают такое развитие событий: если привязанный спутник окажется на чуть большей высоте, чем геостационарная орбита, и начнет отставать от Земли, она его за канатик сначала немножечко подтянет вперед, а потом он снова отойдет на исходное расстояние от поверхности. Но после этого спутник уже не отстанет от вращения Земли, потому что наряду с гравитацией добавляется сила, которая тянет его вперед, и в сумме они создают более сильное центростремительное ускорение, чем одна только гравитация, а эта более высокая орбита становится геоцентрической.

Так что идея космического лифта может быть прекрасно реализована. Осталось только найти материал для каната, чтобы 36-тысячекилометровый трос выдерживал свой вес плюс вес поднимаемого груза (железо для этого не годится, а вот наноуглеродные трубки могут быть перспективными: плотность их меньше, а прочность больше) – и тогда каждому человеку можно будет подняться на геостационарную орбиту за несколько тысяч рублей, по деньгам это все равно как слетать в соседний город на самолете. И это стразу изменит нашу космонавтику.

К другим мирам

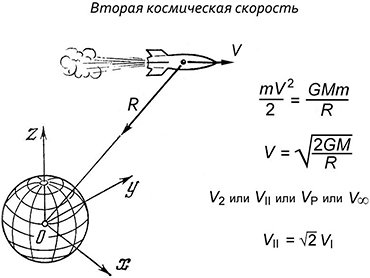Итак, чтобы оторваться от поверхности Земли и выйти в околоземное пространство, надо набрать первую космическую скорость. Следующая задача космонавтики – улететь от планеты. Для этого необходимо достичь скорости, которая называется второй космической. Чтобы рассчитать эту величину, используем закон сохранения энергии: кинетическую энергию тела приравниваем к гравитационной энергии его связи с планетой и находим отсюда значение второй космической скорости: она всего лишь в √2 раз больше первой космической, т.е. у поверхности Земли немногим превышает 11 км/с. Кинетическая энергия – величина скалярная, она не зависит от того, куда направлен вектор скорости, т.е. полетев в любую сторону с такой начальной скоростью, мы покинем планету по параболической траектории.

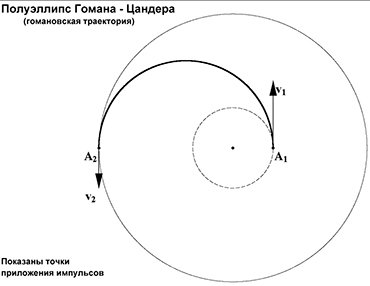Если мы уже на околоземной орбите, а нам надо на Марс или на более дальнюю планету привести корабль, мы его просто «пинаем», т.е. добавляем ему такой импульс, чтобы корабль с круговой орбиты Земли вокруг Солнца вышел на эллиптическую орбиту, в апоцентре которой коснулся орбиты планеты назначения. Если мы правильно рассчитали время старта, планета приходит в ту же точку одновременно с нашим аппаратом. Но встречаются они с разными скоростями: планета движется быстрее, если ничего не предпринять, космический корабль тут же отстанет от нее. Значит, надо еще раз включить двигатели и уравнять скорость. Таким образом, надо придать всего два импульса – и вы оказались у соседней планеты. Такая траектория между планетами называется полуэллипсом Гомана – Цандера (по именам инженеров, рассчитавших эту орбиту).

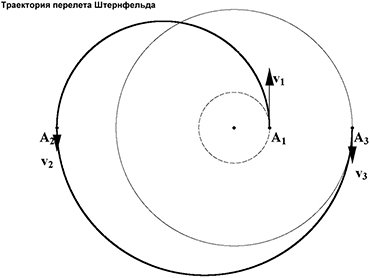Казалось бы, эта простая классическая орбита должна быть энергетически оптимальной, т.е. наилучшей с той точки зрения, как меньше топлива потратить и при этом куда-нибудь подальше улететь. Но – удивительное дело – оказалось, что есть более экономичные орбиты. Открыл их Ари Штернфельд, который увидел, что выгоднее трехимпульсный перелет совершить: сначала улететь дальше той орбиты, куда собираемся попасть, затем, притормозив, спуститься к ней, и потом уже уравнять скорость. Траектория, несомненно, более сложная. Но в сумме эти три импульса (а значит и затраты топлива) оказываются меньше, чем те два для простой полуэллиптической орбиты. Это удивительное открытие в небесной механике Штернфельд сделал, сидя у себя дома, он был вообще очень интересный человек и гениальный космический инженер.

Орбиты спутников

Рассуждения об эллиптической орбите спутников хороши, но природа на самом деле устроена сложнее: та же Земля – не идеальный шар, а сплюснутый, т.е. эллипсоид вращения. Из-за этого сила гравитации вблизи Земли обратно пропорциональна отнюдь не r², а с маленькой добавочкой в показателе степени. Значит, если мы запустили спутник на полярную орбиту (проходящую над южным и северным полюсами), то в таком силовом поле, как мы уже с вами видели на предыдущей лекции, эллипс орбиты постепенно поворачивается, происходит прецессия его оси вокруг центра тяготения.

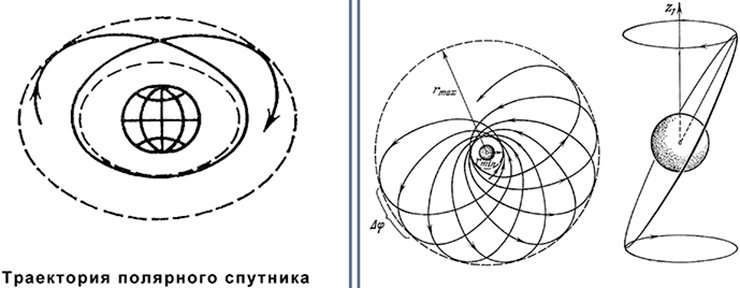
Если орбитальная плоскость расположена под косым углом к экваториальной плоскости Земли, то реальные траектории спутников получаются намного более сложными. Россия обычно запускает спутники на орбиту со средним наклоном к экватору, около 60 градусов (например, спутник телевизионного вещания «Молния»). При этом сама орбитальная плоскость тоже прецессирует, т.е. поворачивается вокруг земной оси. Для точного расчета их орбиты приходится отказываться от теорем Ньютона и все время учитывать неидеальную форму планеты.

Движение двойных звезд

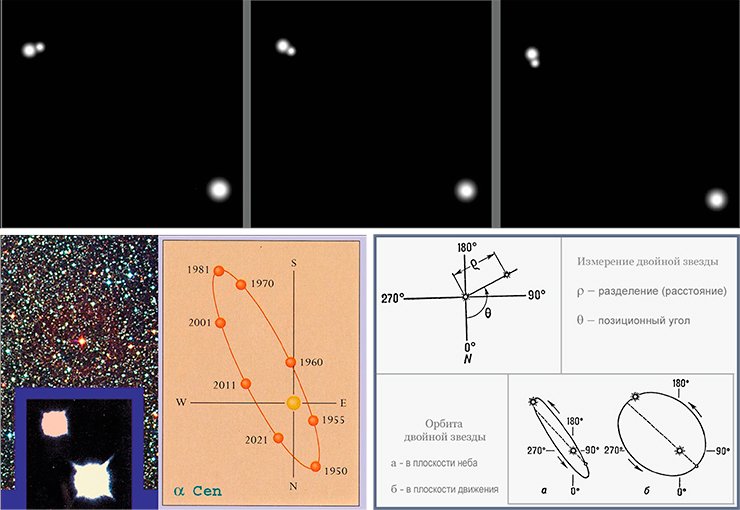
Законы небесной механики описывают движение не только планет и их спутников. Задача двух тел также может быть применена к двойным звездам, которых на небе очень много, даже больше, чем одиночных. Солнце среди них, скорее, является исключением. Ближайшая к нам звезда, Альфа Кентавра, тоже двойная.

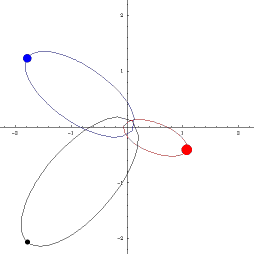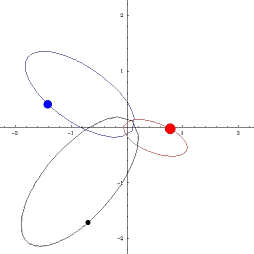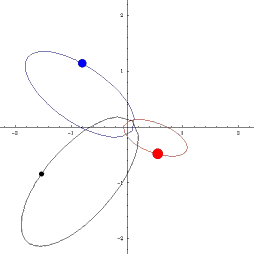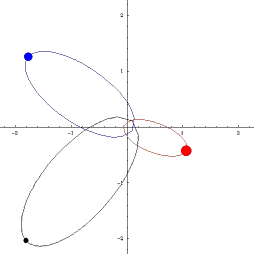
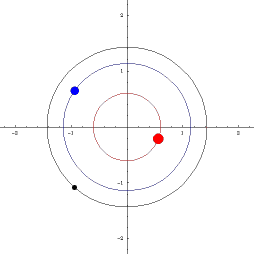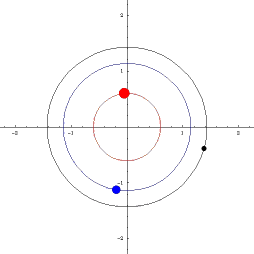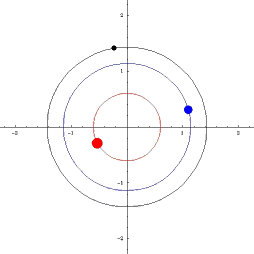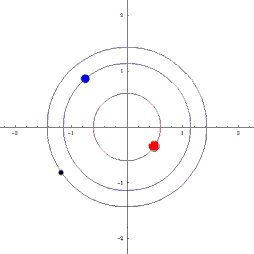
Наблюдая двойную звезду, мы видим, как происходит вращение: оба компонента движутся друг относительно друга. Астрономы всегда измеряют положения близких друг к другу звезд не в какой-то единой системе координат, а просто друг относительно друга – так получается проще. Навели телескоп на одну звезду, более яркую, теперь она у нас всегда в центре отсчета (в начале координат), а вторая по орбите кружится. Но на самом-то деле они обе вокруг общего центра массы «бегают», который невидим и поэтому навестись на него невозможно.

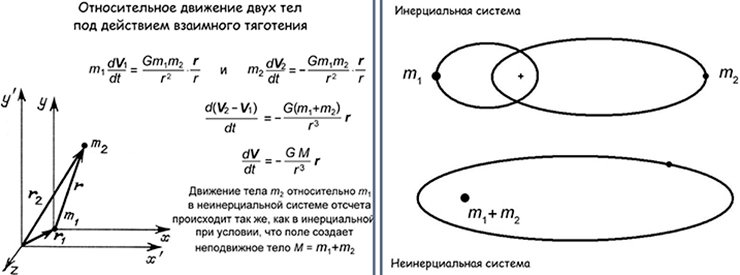
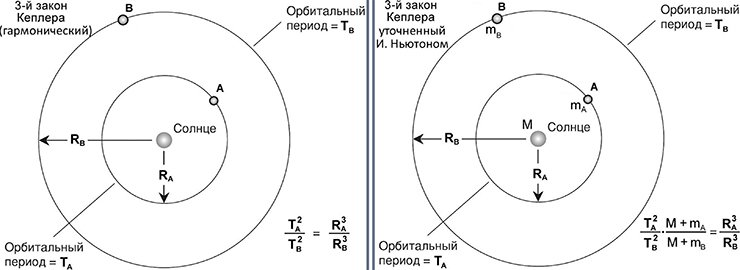
Значит, нам надо модифицировать уравнения небесной механики, из инерциальной системы отсчета перевести в неинерциальную, связанную с одним массивным компонентом. Взяли выражения для векторов обеих скоростей и нашли их разницу, то есть относительную скорость – и оказалось, что она точно так же зависит от всех параметров, как и в законе Ньютона: обратно пропорциональна квадрату расстояния, только теперь в качестве параметра массы фигурирует сумма масс этих двух объектов. То есть при переносе системы координат в одно из тел гравитационно связанной пары все законы небесной механики сохраняются и прекрасно работают, но только как будто бы в этом теле сосредоточена суммарная масса обоих тел, и именно эту суммарную величину мы из наблюдений можем рассчитать по форме относительной орбиты.

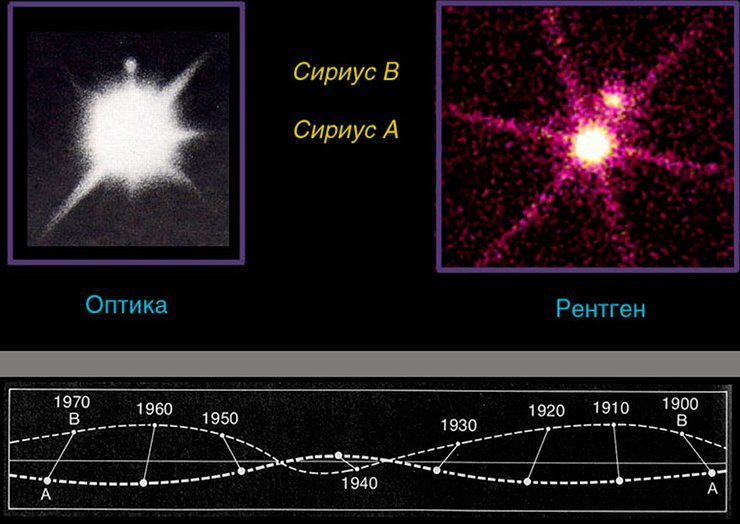
Это не очень удобно, хотелось бы каждое из тел пары «взвесить» отдельно от другого. Редко, но иногда это можно сделать, если удается проследить, как каждое из них свою траекторию на небе выписывает. Например, известная звезда Сириус тоже двойная, у нее есть яркий компонент и маленький спутничек, и астрономы отследили на небе их траектории вдоль центра масс, который по прямой движется. По соотношению расстояний до центра масс, применив третий закон Кеплера, мы узнали, что меньший компонент Сириуса вдвое легче более массивного.

Вот еще интересная проблема для размышления и хорошая задачка для физиков: представим, что в Солнечной системе вдруг пропал центральный объект, Солнце. Убежать оно, конечно, не может, поэтому предположим, что оно взорвалось (вообще-то, взрыв Солнца маловероятен, но отнюдь не исключен) и моментально раскидало свою массу во все стороны далеко-далеко. Вопрос: а сохранится ли Солнечная система? Или планеты разлетятся на все четыре стороны?

Небесная троица

До этого мы говорили только про два взаимодействующих тела, а теперь перешли к более сложной проблеме: три тела. Ну и, казалось бы, что тут такого особенного, что может измениться? А вот небесные механики работали несколько столетий над тем, чтобы создать аналитическую теорию движения трех тел… Работали-работали – и доказали, что это невозможно. Аналитическая теория – это комплекс уравнений, в которые вы подставляете свои параметры и момент времени, какой вас интересует, и вычисления по ним выдают вам координаты, где ваши тела находятся и с какими скоростями они движутся.

Но нашелся человек, Карл Зундман, который создал-таки эту теорию. Казалось бы, ура – нобелевскую премию ему надо дать! Однако не дали, и вот почему. Он эти уравнения записал в виде бесконечных рядов, которые так медленно сходятся, что для того, чтобы хотя бы на год вперед рассчитать положения Луны, Земли и Солнца, надо просуммировать 10⁸⁰⁰⁰⁰⁰⁰ членов. Представьте, что это за фантастическое число: всем компьютерам мира не под силу обработать такое количество данных, потому что в доступной нашему наблюдению Вселенной примерно 10⁸⁸ протонов, а здесь в показателе степени миллионы! Так что теория хоть и есть, но пользоваться ей совершенно невозможно.

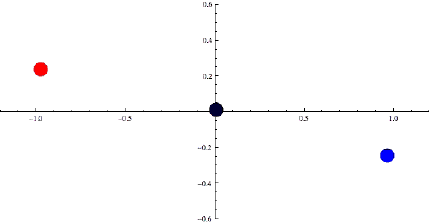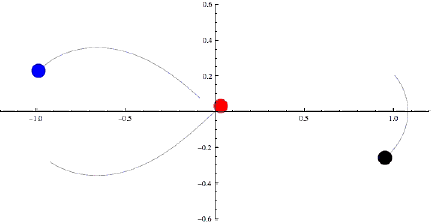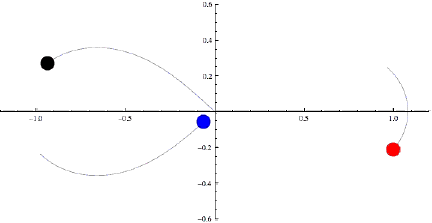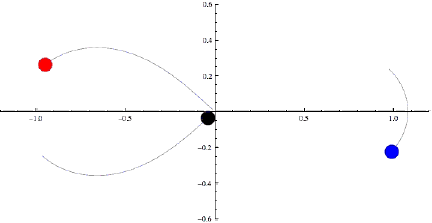
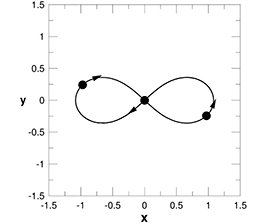
Вообще-то, можно найти конфигурации из трех тел, эволюцию которых можно предсказать. Например, создать искусственно троицу, которая совершает периодическое движение. И тогда посмотрел на один период, а потом копируй его на бесконечно количество последующих периодов. Недавно придумали очень изящную конфигурацию из трех тел одинаковой массы, которые будут летать друг за другом «по восьмерке».

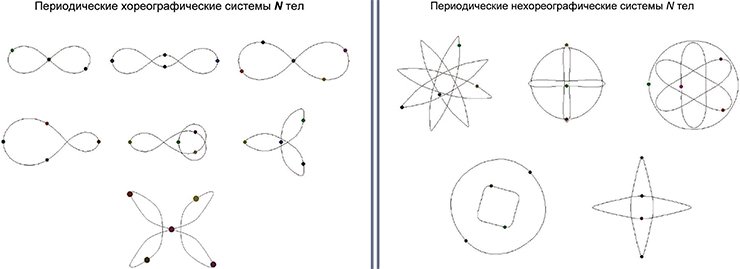
Формально во всех этих случаях тела будут повторять свой циклический путь бесконечно долго, но движение это очень неустойчивое: стоит чуть-чуть, на мизерную величину его нарушить, как система начнет разбалтываться и приведет к хаотическому движению. Даже ошибки компьютерного счета приводят к тому, что траектории начинают расходиться и через несколько периодов обращения система рассыпается. А устойчивого периодического движения тел, количество которых больше двух, не бывает.

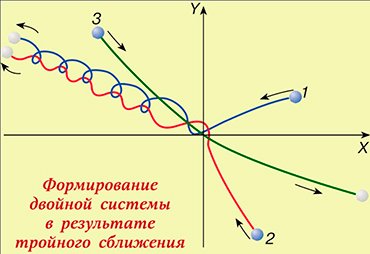В общем случае реализуется такая ситуация: возьмем три массивных тела и отпускаем навстречу друг другу. Сближаясь, они, естественно, сильнее притягиваются друг к другу и в небольшой окрестности бурно взаимодействуют. В большинстве случаев при этом два тела объединяются в двойную систему и начинают по стабильным эллиптическим орбитам летать бесконечно долго, а третье тело уносит избыток энергии – два тела связались, а потенциальная энергия связи перешла в виде кинетической к третьему телу, которое как из пушки вылетает из области взаимодействия. Это обычный результат гравитационного взаимодействия трех тел.

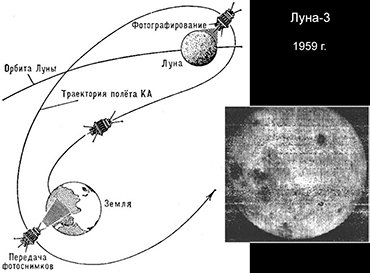Почему задача трех тел очень важна? Это задача жизненная: с Земли продолжают запускать космические аппараты на Луну (например, обратную сторону Луны фотографировать), и надо рассчитывать траекторию полета такого космического аппарата. Решают ее только численно, на компьютерах, шаг за шагом. Правда, очень часто можно сделать упрощающие предположения.

 Например, разумно предположить, что среди этих трех тел только два массивные, а третье по сравнению с ними невесомое, т.е. они его притягивает, а оно на них не влияет. Второе упрощение: пусть все они движутся в одной плоскости, то есть легкое тело летает в орбитальной плоскости первых двух. Третье упрощение: пусть массивные тела относительно своего центра массы движутся по круговым орбитам. И вот когда все эти упрощения мы принимаем во внимание, получается задача, которую уже можно решать аналитически, она называется ограниченной круговой задачей трех тел. Тогда можно перейти в систему координат, связанную с их вращением, чтобы они не бегали у нас на бумаге, а оба стояли на месте на одном и том же расстоянии друг от друга, а остальная Вселенная крутилась бы вокруг них.

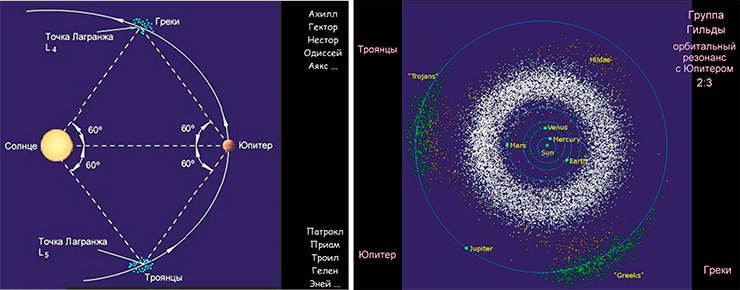
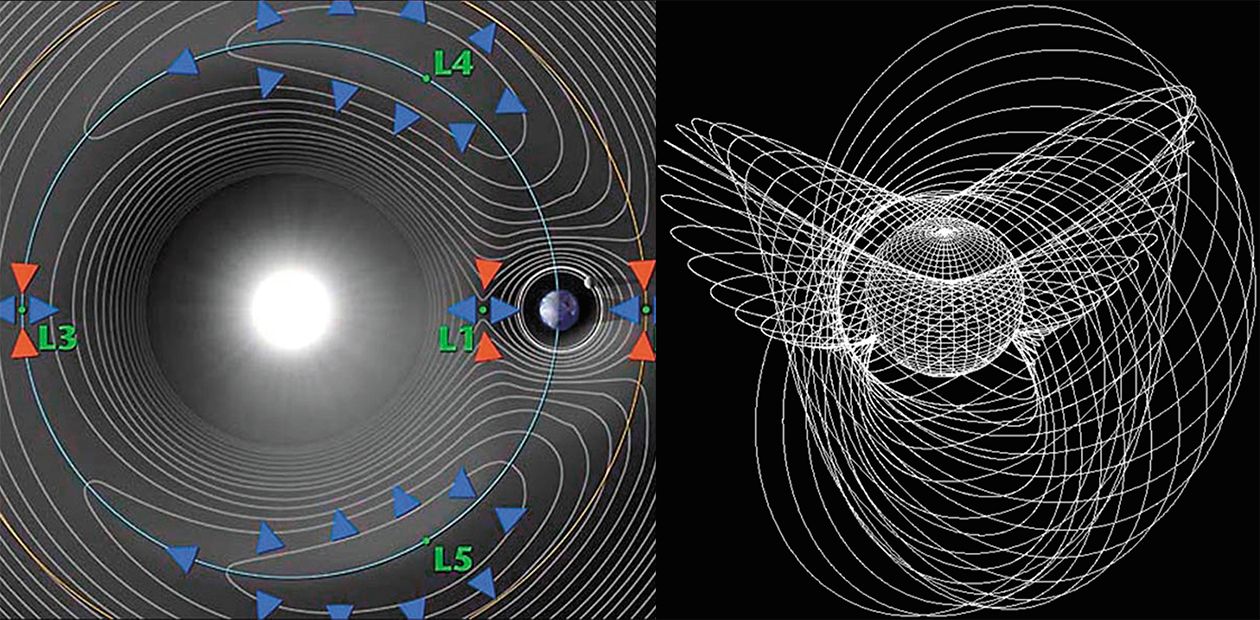
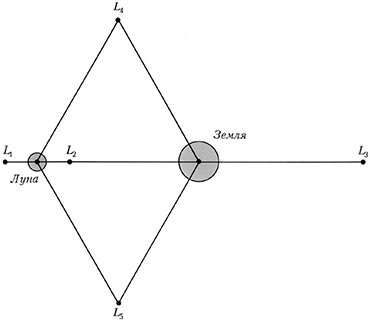Но если вращается система координат, то в ней появляются центробежная и кориолисова силы, их надо ввести в эту систему соответствующими слагаемыми в уравнениях. И оказывается, что в такой системе есть 5 точек, где третье легкое тело может оставаться неподвижным относительно двух массивных (это означает, что в обычной системе координат оно будет обращаться вокруг центра масс синхронно с ними). Три из этих точек – на соединяющей массивные тела линии – еще Эйлер обнаружил, а две другие – при вершинах равносторонних треугольников – Лагранж, но всех их называют точками Лагранжа и обозначают буквой L.

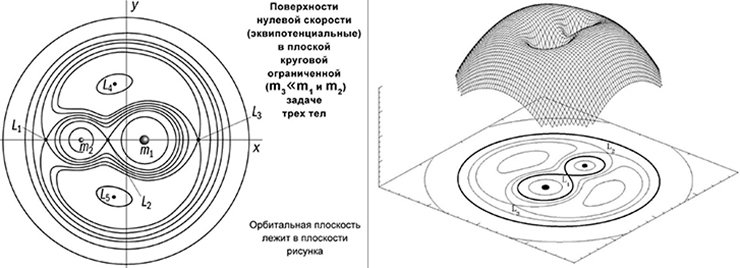
Если нанести на плоскость линии равного потенциала (гравитационного плюс центробежного), то на такой картине мы сразу увидим области контроля гравитации одного и другого тела, область их совместного «контроля», а также области всех пяти точек Лагранжа. Лучше на это смотреть в объемном эскизе, для этого надо построить эквипотенциальную поверхность, в которой будет две гравитационных ямы, вокруг которых центробежный потенциал дает нам скат по всем направлениям, потому что при отдалении от массивных тел центробежная сила тебя выкидывает из этой системы. На цветной иллюстрации это выглядит понятнее, пять локальных максимумов поверхности – это точки равновесия. Но, надо сказать, равновесие это совсем неустойчивое, поэтому зависнуть в этих точках довольно сложно: чуть-чуть отклонился в любую сторону – и сразу же начнет от них относить.

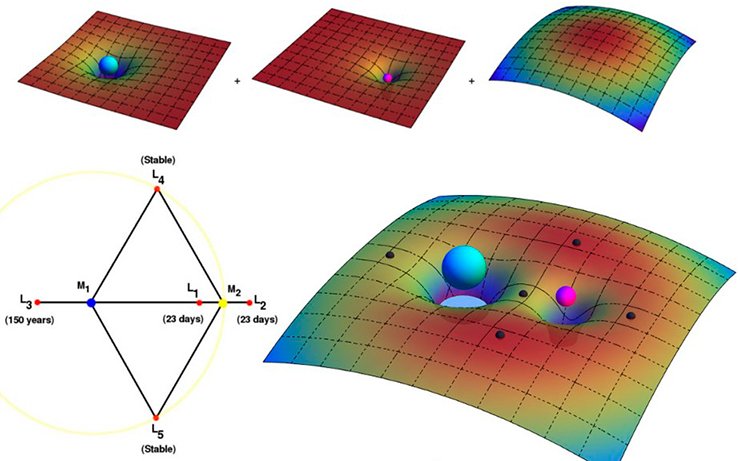
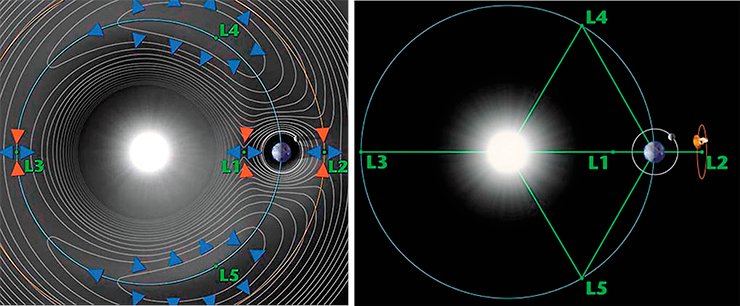
Тем не менее, в природе довольно часто, да и в технике тоже, определение точек Лагранжа играет большую роль. Луна движется внутри области гравитационного контроля Земли, но не очень далеко от пограничной линии, так что устойчивость Луны не слишком велика, она не очень сильно привязана к Земле. С другой стороны, космические аппараты часто запускают в разные точки Лагранжа, потому что там очень удобно «подвесить» аппарат. Так, в точке L₁ он будет всегда смотреть на Солнце, а антенна для связи с Землей при этом постоянно направлена на Землю, в точке L₄ он одновременно будет видеть и Солнце, и Землю с Луной и в то же время подальше от них находиться, т.е. разные точки играют разную роль. Единственная точка L₃ пока не используется, хотя она очень интересна: если туда спутник поместить, то он будет ту полусферу Солнца наблюдать, которую с Земли не видно. Но как с ним связываться? Радиосигнал сквозь Солнце не проходит, поэтому надо будет ретранслятор какой-то сделать.

Эквипотенциальная поверхность системы двух массивных тел, проходящая через точку L₁, ограничивает две области пространства, контролируемые соответствующим центром притяжения. Их называют полостями Роша, по имени французского математика, который сделал расчеты. Если легкое тело приближается к окрестности этой точки, то оно будет двигаться по довольно замысловатой траектории. Например, мы запустили спутник к Луне, он перескакивает в область контроля Луны, делает там несколько пируэтов, а затем снова оказывается спутником Земли. Но за границы эквипотенциальной поверхности он выйти не может, потому что энергии ему для этого не хватает, он заперт в совместном гравитационном поле двух тел.

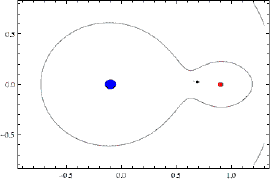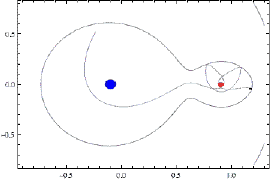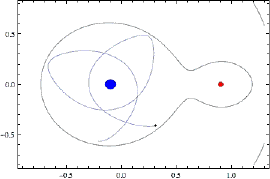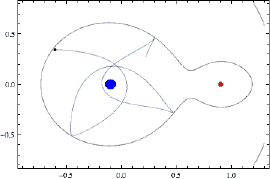
 В нашей планетной системе два самых массивных тела – это Солнце и Юпитер. В точках Лангранжа этой пары реализовалась интересная ситуация: там скопилось очень много астероидов. Попадая в эту область относительной устойчивости, астероиды остаются там надолго, на миллионы лет, а уходят они оттуда очень медленно и поэтому их концентрация там весьма высока. Эти две группы астероидов постоянно сопровождают Юпитер на его орбите, доказывая, что Лагранж правильно сделал свои вычисления: одна группа (условно названная «Греки») на 60° впереди Юпитера, другая («Троянцы») – на 60° позади него, и в каждой по нескольку тысяч астероидов.

Гравитационная праща

Есть еще одна важная вещь, связанная с задачей трех тел: гравитационный маневр, который часто используют для доразгона космических аппаратов. Например, чтобы забросить зонд к дальним планетам – Нептуну, Урану, Плутону и дальше, – используют гравитационное притяжение встречающейся по пути планеты. В принципе, идея та же, что и в обычной механике: если вы маленький мячик катнете навстречу катящемуся тяжелому, при отскоке скорость маленького увеличится – это следствие закона сохранения импульса. То же самое случается, когда планета летит вперед, а зонд приближаясь к ней, облетает планету и при этом приобретает дополнительный импульс. Чтобы осознать причину этого, можно рассуждать так: находясь на этой планете, мы увидим, что зонд приближается к нам на большой относительной скорости (равной скорости планеты плюс скорость зонда), потом он развернул свой вектор скорости и удаляется с таким же модулем относительной скорости. Но в неподвижной системе координат получается, что скорость планеты добавилась к нему два раза: сначала на встречном курсе, потом на уходящем.

Значит, при разумном планировании траектории можно увеличить скорость зонда в пределе на удвоенную орбитальную скорость планеты, хотя удается такое редко. Так, в 1977 году запустили два космических аппарата, «Вояджер-1» и «Вояджер-2», очень красивый был эксперимент. Оба зонда облетели Юпитер и Сатурн, получив от этих планет такие толчки (и, кстати, подходящие направления скорости), что и тот, и другой вылетели из Солнечной системы. Ракета их так разогнать не могла, именно влияние Юпитера и Сатурна позволило одному сразу покинуть Солнечную систему, а другому – по пути еще посетить Уран и Нептун. Вот такой грандиозный тур они сделали – а все благодаря точному расчету траектории полета.

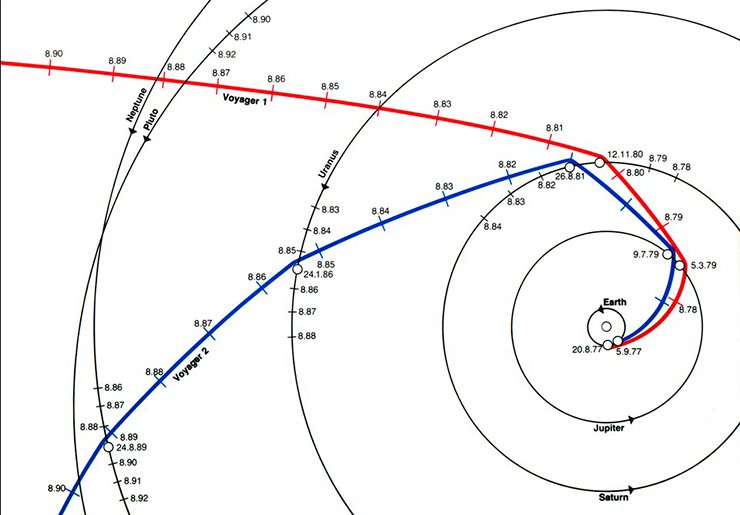
Кстати сказать, первый зонд запустили без надежды на точный расчет, он посетил только Юпитер и Сатурн, но к Урану и Нептуну не попал. А со вторым уже ясно стало, что можно рискнуть, просто его надо было круче завернуть. Чтобы сильнее повернуть вектор скорости, надо пролететь ближе к планете. И чтобы она сильнее притягивала, куда, вы думаете, его запустили? Его направили в щель между внутренним кольцом Сатурна и поверхностью планеты. Тогда еще не знали, что это место тоже заполнено веществом, думали, что там пустота. А теперь мы понимаем, что риск был огромный: он там запросто мог стукнуться обо что-нибудь. Но зонду повезло, он беспрепятственно проскочил в эту щель, под действием планеты разогнался, сильно повернул – и дальше полетел куда надо.

Траектория Луны

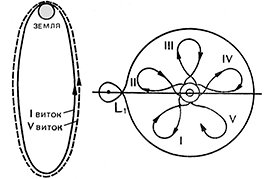
Обычно в учебниках говорится так: Луна обращается вокруг Земли, а Земля – вокруг Солнца, поэтому траектория Луны вдоль орбиты Земли выглядит вот так – и при этом рисуют циклоиду. Начинающий астроном именно так бы изобразил траекторию Луны, как она вокруг Земли ходит и петельки наворачивает. Но на самом деле это не так, и подобную картину мы можем легко опровергнуть, сделав простой расчет.

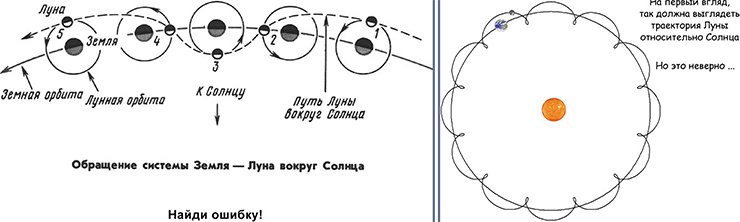
Для физиков не должно быть сомнений в том, что траектория любого тела всегда вогнута туда, куда его тянет равнодействующая (суммарный вектор) всех сил. Давайте проверим, что сильнее притягивает Луну – Земля или Солнце. Это очень просто: сравниваем две гравитационные силы, они равны отношению массы к квадрату расстояния (см. предыдущую лекцию). Луна примерно в 390 раз ближе к Земле, чем к Солнцу. А отношение масс Земли и Солнца – около 3∙10⁻⁶, т.е. Земля в 333 тыс. раз легче Солнца. Поставляем в формулу – и получаем, что сила притяжения Луны к Солнцу вдвое больше, чем к Земле. Факт неожиданный: ведь если Солнце притягивает сильнее, чем Земля, то Луна должна быть спутником Солнца, а не Земли, разве не так? Отчего ж тогда она вокруг нас бегает, если Солнце ее вдвое сильнее притягивает? С этим надо разобраться.

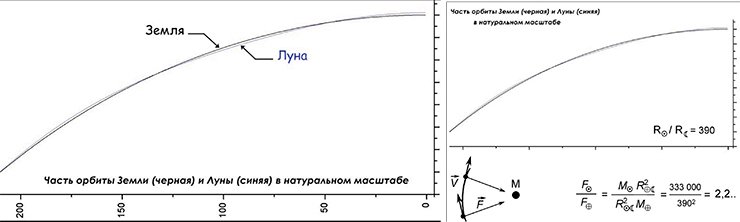
Если мы построим график движения Земли и Луны в реальном масштабе, то увидим, что знак кривизны траектории Луны никогда не меняется, кривая всегда вогнута вовнутрь, и равнодействующая сила всегда направлена внутрь орбиты, т.е. в сторону Солнца. Почему же Луна от Земли не отрывается и не становится спутником Солнца? А вот почему: и Земля, и Луна притягиваются Солнцем практически одинаково, но, чтобы оно было способно оторвать Луну от Земли, нужно, чтобы разница между ускорениями Земли и Луны к Солнцу была больше, чем ускорение Луны к Земле!

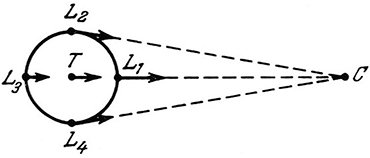Вот если бы радиус лунной орбиты был, скажем, всего лишь вчетверо меньше, чем радиус орбиты Земли, то Луна действительно выписывала бы «школьные» пируэты. А когда мы начнем увеличивать размеры земной орбиты, удалять Солнце, приближая отношение параметров к истинным, постепенно дело приходит к тому, что орбиты Луны и Земли становятся практически неразличимыми – обе они спутники Солнца. И лишь потому, что они находятся близко друг к другу, Земля не отпускает от себя Луну, обе эти планеты (Луна тоже планета; точнее, планета-спутник) практически одинаково «падают» на Солнце, т.е. почти с одинаковым ускорением движутся относительно Солнца, а разница этих ускорений так мала, что Земля способна контролировать положение Луны рядом с собой. 

В заключение рассказа хочу посоветовать вам книги для дополнительного чтения. Самые простые для понимания – это «Парадоксы космонавтики» вышеупомянутого А.А. Штернфельда и «Цели и пути покорения космоса» Р.Г. Перельмана (не Якова Исидоровича, который «Занимательную физику» написал, и не Григория Яковлевича – знаменитого математика, а другого Перельмана, Романа Григорьевича, инженера). Следующая пара книг – уже с математическими формулами: это «Механика космического полёта» В.И. Левантовского и «Основы космонавтики» М. Фертрегта. Далее идут серьёзные справочники по небесной механике – «Введение в астронавтику» Г. Руппе и «Космонавтика» Е.В. Тарасова. И, наконец, вышедший в двух изданиях бестселлер «Очерки о движении космических тел», автор которого, Владимир Васильевич Белецкий, – совершенно удивительный человек и фантастический лектор. Он абсолютно глухой, но, впервые побывав на его лекции, я об этом даже не догадался, настолько хорошо он рассказывал. И книгу написал потрясающую – ни о какой более захватывающей про небесную механику мне не известно.