Основы небесной механики

«Культурный человек лишь слегка обгрызает кости, а потом бросает их под стол»
(цитата из мыслей пёсика Фафика)

За одну лекцию изучить небесную механику – дело нереальное, поэтому знакомиться с ней мы будем на таком уровне, как подсказывает нам эпиграф. Он взят из замечательной книжки «Очерки о движении космических тел» Владимира Васильевича Белецкого, это один из наших сильнейших небесных механиков. Книжку я вам советую почитать, картинки там прекрасные, формулы тоже, и вообще от ее чтения получаешь наслаждение. Итак, сегодня мы будем знакомиться только с основными идеями и простейшими формулами.

Есть, к примеру, у нас планета (или любое другое небесное тело). Она движется и развивается под действием каких-то сил: гравитационных и негравитационных (светового давления, прямых ударов других тел). Есть также внутренние силы, которые вызывают деятельность вулканов, движение материков. Но сегодня мы будем говорить только о гравитации. И тему гравитации мы поделим пополам.

Первая часть представляет самый простой подход к изучению движения небесных тел. Поскольку большие небесные тела практически шарообразны (о причинах этого я скажу ниже), их притяжение друг к другу можно описать притяжением материальных точек, расположенных в центрах тел и содержащих всю их массу (это мы тоже сегодня докажем). В этом случае неплохо работает очень простой, известный даже школьникам закон Ньютона. Правда он не вполне правильный, общая теория относительности (ОТО) корректнее описывает гравитацию, но для нас это пока несущественно.

Есть более тонкий подход. Он учитывает, что тела являются протяженными, и каждая их конкретная точка находится на разных расстояниях от соседнего тела. Значит, в общем случае нельзя одно и то же расстояние в формулу для гравитационной силы подставлять, надо учитывать зависимость гравитационной силы от расстояния до притягивающего тела. Это уже второе приближение к истине, и называется оно теорией приливов. Приливы – вообще штука интересная и очень важная. Но об этом – на следующей лекции. А сегодня будем говорить только о небесной механике.

Самая слабая сила

Давайте посмотрим на запись закона всемирного тяготения Ньютона, связывающего силу притяжения F между двумя материальными точками, в которых сосредоточены массы M и m, разделяемые расстоянием R: F = G∙M∙m/R² – и осознаем одну неприятную вещь. А именно: значение коэффициента пропорциональности G = 6,672∙10⁻¹¹ H∙м²/кг², называемого гравитационной постоянной, очень маленькое в знакомых нам единицах измерения (метры, килограммы, ньютоны). Если сто грамм на ладошку положить (полстакана воды) – это будет сила тяжести в один ньютон.

Прикинем, каковы гравитационные силы. Пусть каждый из вас весит порядка ста килограммов (не хочу никого обидеть, просто округляю для простоты вычислений) и находитесь за партами друг от друга на расстоянии одного метра. Подставляем эти значения в формулу и находим силу нашего взаимного притяжения: F ∿ 10⁻¹⁰∙100∙100/1² = 10⁻⁶ (Н), это одна миллионная от ста граммов или одна десятая доля миллиграмма. Это притяжение друг к другу вы не ощущаете, хотя закон говорит, что оно есть. Т.е. гравитация – самая слабая из всех природных сил, она практически неощутима. Почему же мы чувствуем, что нас к сиденью притягивает?

Очень малое значение гравитационного коэффициента говорит о том, что только большие массы могут ощутимо взаимодействовать друг с другом. Например, масса всей Земли – она большая, поэтому мы ощущаем притяжение к ней. А сидя рядом друг с другом, даже и не догадываемся, что существует сила гравитации.

Есть и другая особенность. Если сравнить значение этой физической константы с другими, например, зарядом электрона e = 1,60217739∙10⁻¹⁹ Кл, что сразу бросается в глаза? Огромная разница в количестве значащих цифр. Естественно задать вопрос: электроном, значит, физики интересуются, измерили его заряд до десяти значащих цифр, а гравитацию почему-то проигнорировали? Почему они не хотят измерить точно?

Отнюдь – хотят, но не могут. Ведь в формулу наряду с G входит величина M, но откуда мы можем знать массу Земли, кто-то ее взвешивал? Ее ведь на весы не положишь. Ускорение свободного падения a = F/m, а значит, и произведение G∙M мы можем измерить точно. Но чтобы отделить их друг от друга, надо действовать как-то по-другому.

Например, можно сначала взвесить тело на весах, а потом посмотреть, как оно притягивает соседей. Для этого «древний» английский физик Дж. Мичелл (1793) придумал крутильные весы – очень чувствительный прибор, с помощью которого другой английский физик Г. Кавендиш (1798) впервые измерил силу гравитационного притяжения двух лабораторных тел и определил значение гравитационной постоянной Ньютона. В нашем институте (Государственный астрономический институт им. П.К. Штернберга, МГУ) сделали такую же и потом очень долго мучились, чтобы решить типичную для физиков проблему: отделить от изучаемого явления все паразитные эффекты.

Сначала в этой константе была уверенно известна только одна значащая цифра, в XIX веке узнали вторую, в середине XX века третий знак появился, совсем недавно – четвертый. Пятый еще пока пытаются выяснить: даже при использовании самых лучших методов он у всех разный определяется, большей точности достичь не получается.

Движение двух тел

Единственное тело в абсолютной пустоте будет лететь по прямой, потому что на него никакие внешние силы не действуют – этот случай тривиальный и неинтересный. А простейшей задачей небесной механики считается задача двух гравитационно взаимодействующих тел. Но ее можно еще упростить, если взять одно тело очень массивное, а другое очень маленькое. Малое тело движется под влиянием центростремительного ускорения, а большому безразлично, что там вокруг него бегает, фактически оно не чувствует чужого присутствия и поэтому неподвижно. Эта ситуация называется задачей одного тела в центральном гравитационном поле.

Если начало системы координат совместить с массивным телом, то вследствие его неподвижности такая система координат будет инерциальной. И это может оказаться очень полезным. Например, для космического аппарата мы можем записать, что действующее на него центростремительное ускорение равно отношению силы гравитационного притяжение к его массе. Если он обращается на достаточно дальней круговой орбите, то, сделав простое преобразование этой формулы, можно однозначно связать орбитальный период с массой притягивающего тела. Собственно говоря, это единственный надежный метод для определения массы планеты.

Но задача становится сложнее, когда спутник находится близко к планете – при этом уже нельзя пренебрегать ее размером и формой. Казалось бы, эта задача очень сложная, потому что для решения надо вычислить притяжение спутника к каждой точке планеты и сложить векторы сил. Также и для геофизика, который интересуется внутренностью планеты и хочет узнать, какова гравитация на нужной глубине: ему надо бы вычислить притяжение ко всем точкам внешней части и ко всем точкам внутренней части. К счастью, еще Ньютон доказал две простые, но очень полезные теоремы, значительно облегчающие вычисления, – и за это ему спасибо.

Первая теорема говорит о том, что если у вас есть однородная по плотности сферическая оболочка, то внутри нее гравитация отсутствует и ускорение везде равно нулю. Доказательство можно продемонстрировать на пальцах. Для этого помещаем в произвольное место полости пробный шарик и смотрим, какие силы на него действуют со стороны двух диаметрально противоположных сегментов. Площади и массы обоих сегментов прямо пропорциональны квадрату расстояния, а сила обратно пропорциональна квадрату расстояния, значит, оба оказывают одинаковое влияние на эту точку, но противоположно направленное, то есть силы уравновешиваются.

Таким образом, где бы ни находилось тело внутри оболочки, оно пребывает в состоянии невесомости. Даже лучше: когда вы свободно падаете без опоры, то вы тоже испытываете невесомость в течение короткого времени, пока не упали, а в полости вообще нет гравитационного поля и "падать" там можно бесконечно долго.

Теперь из последовательности таких оболочек мы можем собрать всю планету целиком и понять, что для вычисления ускорения свободного падения в какой-то внутренней точке достаточно учитывать только более глубокие слои. А принимать во внимание наружные по отношению к рассматриваемой точке слои, которые лежат поверх, т.е. ближе к поверхности, нет необходимости, потому что они никакого влияния не оказывают. В частности, это приближение верно для Земли, у которой плотность к центру растет, при этом на каждой выбранной глубине она под любой точкой поверхности почти одинакова. Геофизики молятся на эту теорему Ньютона, потому что она позволяет им легко вычислять гравитационное поле внутри шаровидных (сферически симметричных) космических тел. Но для тел другой формы это уже не справедливо.

Вторая теорема Ньютона касается притяжения однородной сферической оболочкой тела, расположенного снаружи. Оказывается, в этом случае оболочка на внешнее тело действует так же, как и материальная точка с той же массой в центре сферы. Для доказательства нужно рассчитать гравитационный потенциал в зависимости от расстояния от этой точки до кольца, вырезанного в сфере. При этом кроме теоремы косинусов ничего более сложного знать не обязательно.

Из серии сферических оболочек можно собрать массивную шаровидную планету или звезду, а, значит, в ее поле тяготения движение всех малых объектов – как спутников, так и мимо пролетающих тел – можно рассчитывать в приближении, будто вся масса шара сосредоточена в центральной точке. Этот факт очень важен для астрономов, потому что все достаточно крупные космические тела почти сферичны, если они не очень быстро вращаются (иначе они становятся эллипсоидами и эти теоремы перестают работать).

Теперь давайте представим себе мир, в котором гравитация не по Ньютону устроена. С помощью простенькой компьютерной программы интегрирования уравнений движения попробуем "поиграть" с законом гравитации, меняя показатель степени m при расстоянии (Rᵐ) в формуле Ньютона. В классическом случае m = 2. Запускаем пробное тело вокруг точечной массы и получаем ожидаемый результат: пробное тело бегает по одному и тому же эллипсу.

Если сделаем зависимость гравитации от расстояния более жесткой, увеличив показатель степени чуть-чуть, всего на 10%, то вот что получится: вроде бы движение тоже по эллипсу происходит, но он не остается неизменно ориентированным: его ось понемножечку поворачивается, происходит прецессия оси. Теперь возьмем зависимость F(R) немножко мягче ньютоновой, уменьшив m на 25%. При таком законе тоже вырисовывается похожий эллипс, только вращающийся в противоположном направлении. Интересно, что если задать совсем уж невообразимый вариант m = 1 (т.е. F ∿ 1/R), то угловая скорость прецессии оси становится близкой к угловой скорости обращения спутника.

Несмотря на то, что движение кажется хаотичным, можно заметить, что во всех рассмотренных случаях есть границы движения, за которые тело никогда не вылетает. Механики называют такое движение финитным, то есть ограниченным в пространстве. Если бы у нас, например, в законе Кулона показатель степени при расстоянии вдруг "поплыл", то электрон, по крайней мере, не убежал бы от ядра и не упал бы на него. Ну, двигался бы немного более хитро, чем в наши дни, но с этим жить можно. Главное – что атом остался бы стабилен, не распался бы.

Эти численные эксперименты – вовсе не блажь. Дело в том, что ньютонов закон действителен только в слабых гравитационных полях; он является, так сказать, лишь первым приближением к реальности. А если вы возьмете уравнения общей теории относительности и на их основе попытаетесь получить ньютоновское приближение, то к основному компоненту G∙M/R² добавятся поправки – слагаемые, растущие с увеличением потенциала гравитационного поля. То есть в общей теории относительности гравитация более круто зависит от расстояния, чем по Ньютону. Поэтому есть особенность приближения к объектам очень большой массы, но малого размера.

Вот как хитро будут кружить объекты в окрестности черной дыры: на каждом обороте (от апоцентра до апоцентра) эллипс разворачивается на 180°. При этом происходит не медленный дрейф оси, как в ранее рассмотренных случаях, а прыжки сразу на пол-оборота. Так что наши "игры" с законом притяжения имеют смысл: они позволяют моделировать реальное гравитационное поле вблизи массивных, плотных объектов, нейтронных звезд и черных дыр.

А вот теперь я на целую единицу увеличил показатель (m = 3), сделав еще более жесткую по сравнению с ньютоновой зависимость F ∿ 1/R³. Что мы видим: движение становится инфинитным, то есть пространственно неограниченным. Конечно, в принципе можно найти для частицы, находящейся на некотором расстоянии от тяготеющего центра, такую скорость, при которой частица пойдет по круговой орбите. Но это движение будет неустойчивым: стоит на какую-то мизерную долю изменить эту скорость, и частица, двигаясь по спирали, либо упадет на центр притяжения, либо навсегда уйдет от него. А в реальности какие-то случайные флуктуации всегда есть. Следовательно, в таком потенциальном поле ни атомов, ни планетных систем существовать не может.

Доказано (это довольно легко сделать), что в законах, описывающих силовые поля, показатель степени m связан с геометрической размерностью физического пространства: он во всех случаях на единицу меньше, чем размерность пространства. Отсюда следует, что из записи фактических законов Кулона и Ньютона мы можем сказать, что наше пространство трехмерное. И что четвертого пространственного измерения у нас нет, иначе бы все давно бы потеряло устойчивость, потому что атомы бы развалились.

Орбитальные параметры

Когда небесные механики интересуются движением тел, они используют специальную систему координат. В принципе, можно было бы ничего не изобретать и взять декартовы координаты. Что нам нужно задать для частицы, чтобы потом рассчитывать движение по орбите? Начальное положение частицы в пространстве и ее начальную скорость. Это векторные величины в пространстве, т.е. каждая их них имеет три компонента. Итого шесть чисел полностью описывают состояние частицы в пространстве. Больше ничего не требуется, у нас есть формула для вычисления гравитационной силы, действующей на небесное тело, и законы механики позволяют нам рассчитать, как она будет двигаться, т.е. положение и скорость в любой момент времени.

Но реально для небесной механики такой подход чаще всего не реализуется, он слишком сложный. Ведь если у нас есть только один тяготеющий центр, то любая отпущенная на свободу частица, какую бы скорость мы ей первоначально ни задали, под действием гравитации будет летать в плоскости и никуда из этой плоскости не выйдет.

Иными словами, у любой частицы есть своя орбитальная плоскость. Вот с ней и любят работать небесные механики, потому что она сразу уменьшает количество пространственных измерений. По крайней мере, на одно: если мы знаем, что тело движется в плоскости, то перпендикулярную ей компоненту скорости и расстояние можно отбросить. А чем меньше уравнений, тем легче решать.

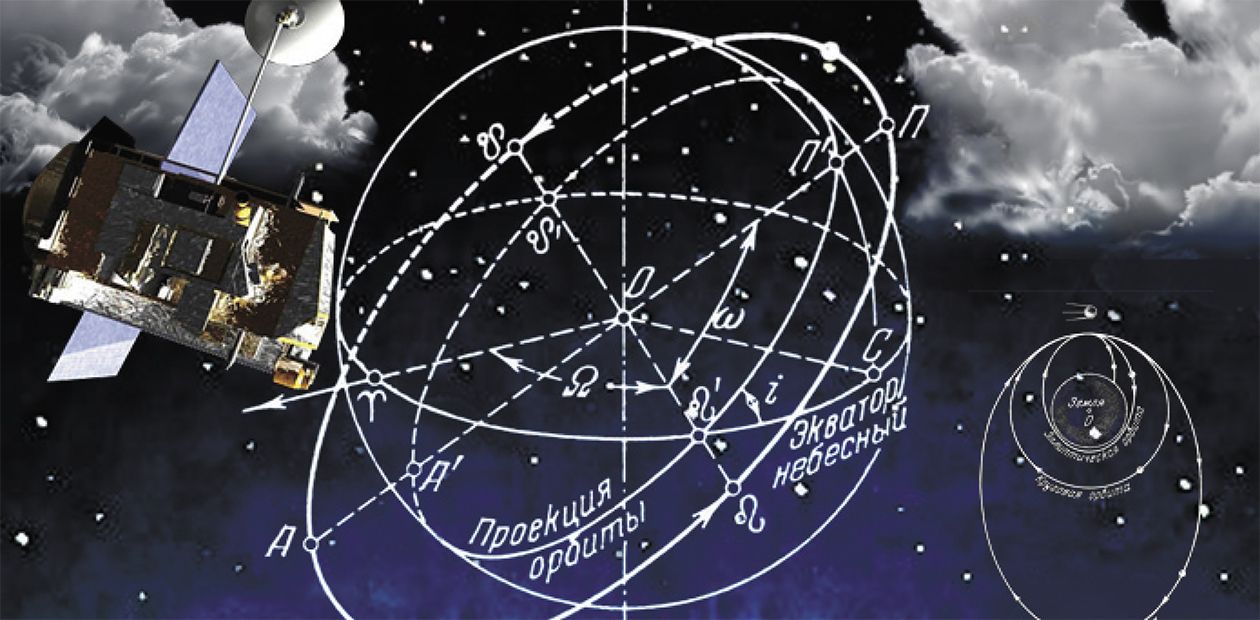
Но надо задать, как орбитальная плоскость рассматриваемого объекта располагается в пространстве. Для этого, естественно, сначала выбирается базовая координатная плоскость, от которой ведется отсчет (обычно это плоскость эклиптики Солнечной системы). Чтобы описать, как в пространстве располагается орбитальная плоскость относительно базовой, надо определить угол, под которым они пересекаются. Этот угол называется наклонение.

Важно не запутаться в терминах, потому что астрономы употребляют два похожих слова: «наклонение» и «наклон», которые означают вовсе не одно и то же. В отличие от наклонения, наклоном называют угол между осью собственного вращения планеты и ее орбитальной плоскости (например, наклон земной оси равен 23,5°).

Пересечение орбитальной и базовой плоскости называется линией узлов. Эта прямая проходит через два узла: восходящий и нисходящий. Восходящий узел – точка, где планета из южной полусферы неба переходит в северную, а нисходящая – где планета "ныряет" из северного полушария в южное. Обозначаются они, соответственно, символами ʆƪ и ƪʆ.

Второй параметр, который надо указать для небесных координат, определяет ориентацию линии узлов в пространстве. Базовое направление мы можем задать на точку весеннего равноденствия, Солнце каждый год через нее проходит. Угол Ω между линией узлов и базовым направлением называется долготой восходящего узла.

Итак, орбитальную плоскость, наклонение и ориентация мы определили. Теперь надо определить характер движения планеты в этой плоскости. В простейшем случае, когда система состоит из одной звезды и одной планеты, она движется по эллипсу. А у эллипса есть только две характеристики: размер и форма. Размер – это длина большой оси, а форму можно определить через параметр эксцентриситет.

Четыре параметра у нас есть, вроде бы достаточно? Ан нет, не достаточно! Сам-то эллипс в орбитальной плоскости как ориентирован? Значит, надо указать угол его ориентации – например, между линией узлов и направлением на перицентр Π (точку орбиты, ближайшую к центру притяжения).

Итак, пять параметров указали, можем ли, наконец, произвести расчет движения планеты в будущее и в прошлое? Нет, нам надо знать, где планета на этом эллипсе находится в начальный момент времени, чтобы начать вычисления. Например, можно задать момент времени, когда она проходит через перицентр или апоцентр, или через какую-то другую определяемую точку – это уже шестой параметр.

Значит, шесть величин задают полный набор начальных условий, ровно столько их было и в декартовых координатах. Но параметры в небесных координатах позволяют проще решать задачу, даже можно аналитически это сделать.

Как летают спутники

Если нам надо рассматривать движение искусственных спутников Земли, то определять базовую плоскость через эклиптику, т.е. брать в качестве базовой плоскость орбиты нашей планеты особого смысла нет. Ведь спутники всегда летают не очень далеко от Земли, им нет никакого дела до того, как она сама движется вокруг Солнца. Поэтому наклонение плоскости орбиты спутников обычно отсчитывают от экватора земного, а не небесного. Плоскость земного экватора в этом отношении очень полезная, потому что планета у нас довольно симметрична относительно экватора, и это упрощает математические расчеты. Остальные параметры определяют аналогично: например, направление линии узлов – как всегда, на точку весеннего равноденствия.

Теперь давайте посмотрим, как могут двигаться спутники после запуска. Берем и подвешиваем тело над Землей и сообщаем ему импульс. Например, по какой линии движется камень, брошенный под углом к вертикали? Школьный учебник утверждает, что по параболе. Но так ли это?

По этой кривой тела движутся в однородном поле гравитации, когда везде ускорение свободного падения одинаково направлено. Но наша Земля – не плоскость бесконечной протяженности (как ее в древности представляли, на слонах и китах лежащей), а шар. Т.е. она притягивает к своему центру как точка (выше мы говорили, что это следует из второй теоремы Ньютона). Поэтому, как бы мы тело ни кинули, оно полетит по эллипсу. Если с маленькой скоростью, то оно упадет, но все равно будет двигаться по дуге эллипса.

Давайте теперь будем бросать тело горизонтально со всё большей и большей скоростью. Сначала они будут ударяться о поверхность Земли, заканчивая свое эллиптическое движение, при этом точка старта будет апоцентром (наиболее удаленная от центра точка эллипса). При некоторой скорости мы, в конце концов, добиваемся, чтобы тело летало по круговой орбите. А если придать еще большую начальную скорость, то оно также полетит по эллипсу, только теперь точка старта станет не апо , а перицентром.

Кстати, в сообщениях ТАСС и других СМИ вам никогда не скажут, каково расстояние перицентра или апоцентра орбиты того или иного спутника до центра Земли. У них своя особенность языка, они говорят в других терминах – "высота полета космического тела", это расстояние от поверхности. На иллюстрации показана взаимосвязь этих величин. Но для физика важно знать истинные параметры эллипса – расстояние от центра тяготения, значит надо не забывать всегда прибавлять радиус Земли.

А что будет, если еще больше будем наращивать скорость? При некоторой скорости мы получим параболическое движение, тело при этом отрывается, уходит в бесконечность и там замирает, потому что в пределе на бесконечном расстоянии скорость будет нулевой. А если еще больше задать начальную скорость, тогда оно улетает по гиперболе и на бесконечности продолжает двигаться, потому что у него есть запас энергии. И, наконец, если мы метнули это тело с бесконечно большой скоростью, то оно уйдет по прямой линии, вообще «не ощущая» гравитации.

Теперь подсчитаем, с какой скоростью надо запустить тело, чтобы оно на круговую орбиту вышло. Если тело движется по кругу, то надо центростремительное ускорение приравнять к отношению силы гравитации к массе тела. Из этого уравнения получаем выражение для скорости, которая называется первой космической. Важно подчеркнуть, что это векторная величина, т.е. эту скорость надо сообщить спутнику обязательно в нужном направлении.

Однако в телерепортаже мы видим, что ракета стартует с космодрома всегда вертикально вверх, а потом говорят, что ракета набрала первую космическую скорость и вышла на круговую орбиту вокруг Земли. Что дальше было бы, если бы она набрала первую космическую в вертикальном направлении? Вышла бы она на круговую орбиту? Конечно, нет – она бы упала обратно.

Кстати, понятие первой космической скорости (называемой также круговой скоростью) v₁ определяют не только у поверхности планеты: поэтому всегда надо уточнять – в каком месте. В формулу входит расстояние до центра планеты; подставляйте сюда другие значения – и вы получите разные значения первой космической скорости. У поверхности Земли или на небольшой высоте (150 - 200 км), где уже почти нет воздуха, она около 8 км/с, но при удалении от Земли она уменьшается обратно пропорционально корню из расстояния.

Итак, если мы придали телу первую космическую скорость точно в направлении перпендикулярном вектору расстояния, то оно выйдет на круговую орбиту. Но если вы ошиблись с направлением, то получим никакой не круг, а эллипс, хотя и модуль скорости был правильный! Это очень большая проблема для инженеров, которые планируют космические запуски: малейшее отклонение – и привет: спутник может даже войти в атмосферу Земли и сгореть. Обратите внимание, когда запуск космической ракеты долго показывают: сначала она вертикально уходит в стратосферу, а потом постепенно поворачивает, поворачивает, поворачивает – и на высоте 50—70 км начинает двигаться уже параллельно поверхности Земли, и ей надо набрать соответствующую высоте первую космическую скорость, иначе она грохнется обратно на планету.

Для тела, равномерно движущегося по круговой орбите, можно легко записать выражения для его кинетической и потенциальной (гравитационной) энергии. Потенциальная энергия отрицательна, потому что это энергия связи двух тел. Полная энергия движущегося с первой космической скоростью тела в точности равна кинетической по модулю, но они имеют разные знаки. Мы эту формулу только для кругового движения вывели, но оказывается, она справедлива для любого движения и для любой системы гравитационно взаимодействующих точек – это называют теоремой о вириале. Это очень важная теорема, особенно для тех, кто занимается изучением одновременного движения многих тел, скажем, в звездном скоплении, содержащем миллионы звезд. Просчитать их движение по отдельности невозможно, разве что на суперкомпьютерах. Но даже не зная индивидуальных траекторий и скоростей, мы всегда можем быть уверенными, что полная и кинетическая энергии этой кучи звезд равны по модулю.

В сущности, вся небесная механика работает сейчас на космонавтику. Но об этом – в следующей лекции. 

Задать вопрос Владимиру Сурдину