IYPT-2012. Дифракция света на запотевшем стекле

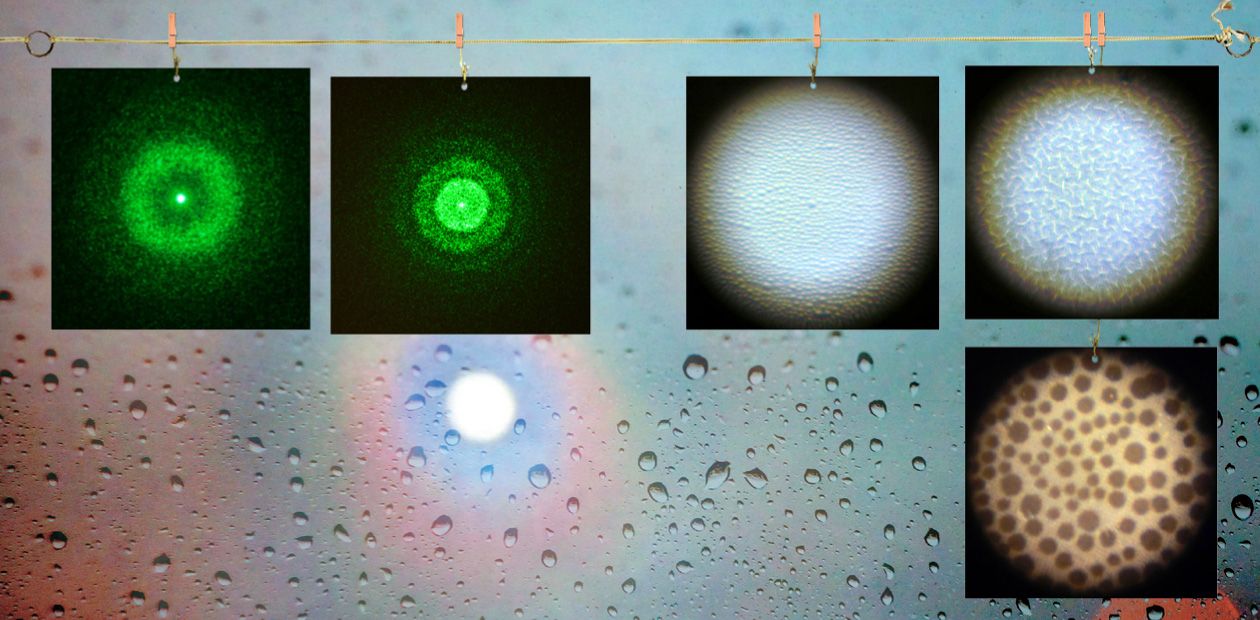
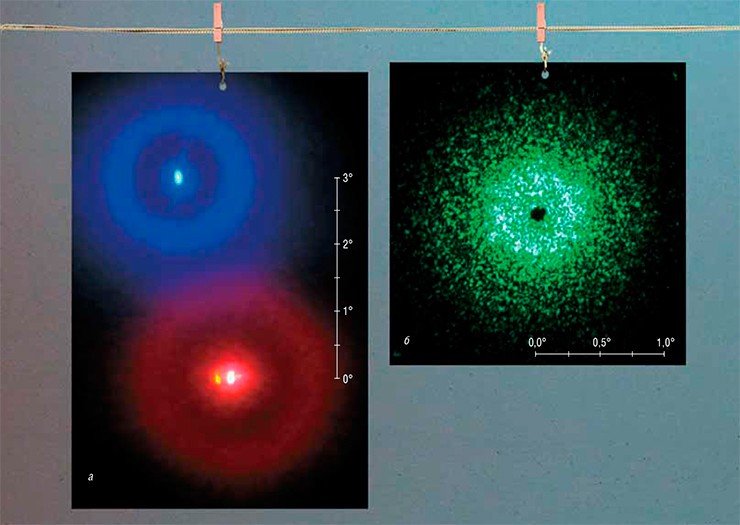
Белый лунный свет, как известно, складывается из лучей разного цвета, поэтому кольца вокруг луны получаются радужными. Чтобы упростить наблюдаемую картину, мы посветили на запотевшее стекло монохроматическим лучом лазера – и получили на экране за стеклом аналогичные кольца.

Похожее явление демонстрируется на лекциях по физике при описании дифракции Фраунгофера на непрозрачном диске. Для этого опыта на стеклянную пластинку наносится порошок ликоподия, который представляет собой сухие споры разных видов плаунов размером около 33 мкм. Если направить луч лазера на такую пластинку, то на экране за ней будут наблюдаться дифракционные кольца. Угловой размер темных колец приближенно определяется по формулы θ ≈ n λ/d (n — порядковый номер темного кольца от центра, λ — длина световой волны, d — размер спор). Если свет рассеивается на нескольких случайно расположенных неперекрывающихся дисках одинакового размера, то картина рассеяния будет в точности такой же, как и для одного диска (Борн, Вольф, 1973).

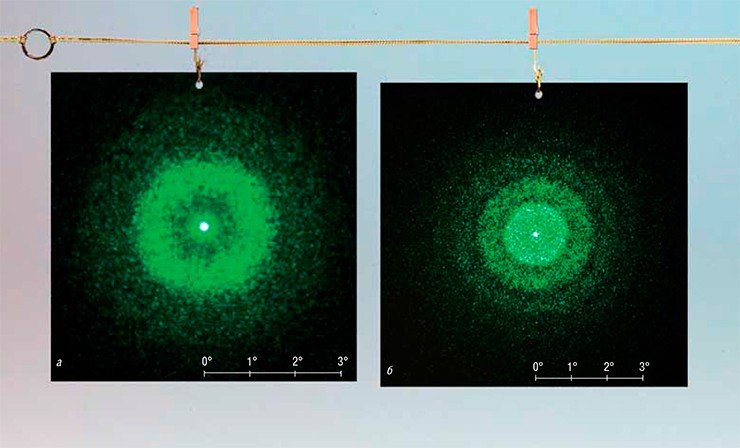
На дифракционной картине света, прошедшего сквозь пластинку со спорами, отчетливо выделяется крупное яркое пятно, которое окружено менее светлыми кольцами. Однако в опыте с запотевшим стеклом на месте этого пятна располагается темный круг, лишь в центре которого видна небольшая яркая точка — она создается лучами, прошедшими через стекло практически без рассеяния.

Задачи Международного турнира физиков IYPT предполагают, что команды сами определяют ход своего исследования. Мы решили, что ключевой частью нашего решения должно стать объяснение различий в двух случаях дифракционного рассеяния — на спорах и на каплях влаги из воздуха, покрывающих запотевшее стекло.

В соседском окружении

Сделав фотографию запотевшего стекла через микроскоп, нам удалось определить размер капель: он оказался в диапазоне 10—20 мкм. Согласно теории дифракции, для капель со средним диаметром (d ≈ 15 мкм) и для зеленого лазерного луча (длина волны λ = 0,55 мкм) характерный угловой размер внутреннего кольца должен быть θ ≈ λ/d = 0,037 рад, т. е. около 2 °. Внешний радиус первого светлого кольца на соответствующей дифракционной картине оказался действительно близок к этому значению.

Но чем отличается стекло с мелкими водяными каплями от стекла со спорами? Споры могут располагаться на стекле более хаотично: между положением отдельных частиц нет никакой связи, они могут перекрываться. Но соседние капли не могут налагаться друг на друга, между ними всегда имеется какой-то промежуток. Это означает, что в расположении капель на стекле обязательно присутствует ближний порядок, схожий с ближним порядком в расположении молекул и атомов в жидкостях и аморфных веществах (Китайгородский, 1952).

Между каплями и спорами имеется еще одно различие: споры непрозрачны, а капли — это маленькие прозрачные линзы. Чтобы показать, что особенности дифракционной картины определяются в первую очередь наличием ближнего порядка в расположении капель, а не их прозрачностью, мы поставили эксперимент, техническая сторона которого была заимствована из статьи Cowley et al. (2005).

Мы импортировали фотографию капель на стекле в графический редактор и обвели каждую каплю по окружности. Таким образом был получен квадратный блок, в котором помещалось около 400 окружностей. Затем его масштабировали и размножили так, чтобы лист размера А4 был весь заполнен окружностями с диаметром 0,5—1,0 мм. После окраски фона в черный цвет изображение распечатали на лазерном принтере.

Эту распечатку затем сфотографировали на черно-белую негативную пленку высокого разрешения, в результате чего белые круги на распечатке превратились в темные круги на фотопленке. Размеры кадра меньше размеров бумажного листа в десять раз, поэтому темные круги на фотопленке имели размер 50—100 мкм – в пять раз крупнее, чем диаметр исходных водяных капель.

Мы ожидали, что, посмотрев через эту фотопленку на источник света, увидим все ту же картину рассеяния, только угловые размеры дифракционных колец будут соответственно меньше по сравнению со случаем стекла с ликоподием.

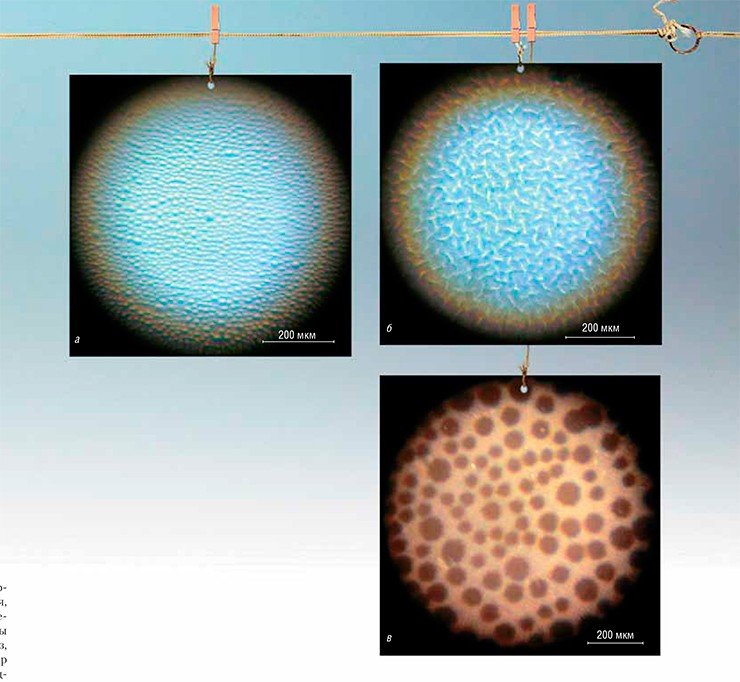
Здесь надо признаться, что правильно провести эксперимент редко удается с первого раза. Поэтому контрастность нашей первой проявленной пленки оказалась такой, что темных кружков на ней вообще не было видно. Но самое неожиданное произошло тогда, когда мы глянули через эту «испорченную» пленку на источник света: к своему удивлению, мы увидели вокруг них точно такие же кольца, как и прежде!

Исследовав эту пленку под микроскопом, мы обнаружили, что она была вся покрыта «червячками» шириной около 25 мкм. Оказалось, что при неправильной обработке желатиновый слой, нанесенный на пленку, может ретикулировать — на высохшем желатине образуется множество мелких трещин. Поскольку прозрачность трещин выше прозрачности желатина, пленка становится оптически неоднородной, и свет дифрагирует на этих неоднородностях. Они обладают ближним порядком, поэтому полученная дифракционная картина оказалась схожей с той, что была получена через запотевшее стекло.

При увеличении выдержки (времени экспозиции) и соблюдении всех условий проявки нам удалось получить хорошее контрастное изображение с четкими кругами. Ди­фракционная картина для такой пленки сохранила основные характерные особенности: центральный узкий нерассеянный пучок света был окружен темной круговой областью, а угловой размер первого светлого кольца (0,3°) также совпал с теоретической оценкой.

В дополнение к этому эксперименту мы создали компьютерную модель фраунгоферовского рассеяния света, которая позволяет получить зависимость интенсивности света от угла рассеяния. В этой модели рассеяние происходило на дифракционной решетке, в которой ширина прозрачных щелей и непрозрачных промежутков между ними случайно менялась в заданных пределах. Кстати, неравномерности интенсивности света, которые видны как на фотографиях картин рассеяния, так и в компьютерных экспериментах, — так называемые спеклы – появляются благодаря ограниченному числу рассеивающих неоднородностей (капелек, кружочков, дифракционных щелей), из-за чего суммирование фазы взаимодействующих световых волн может давать значительные статистические выбросы.

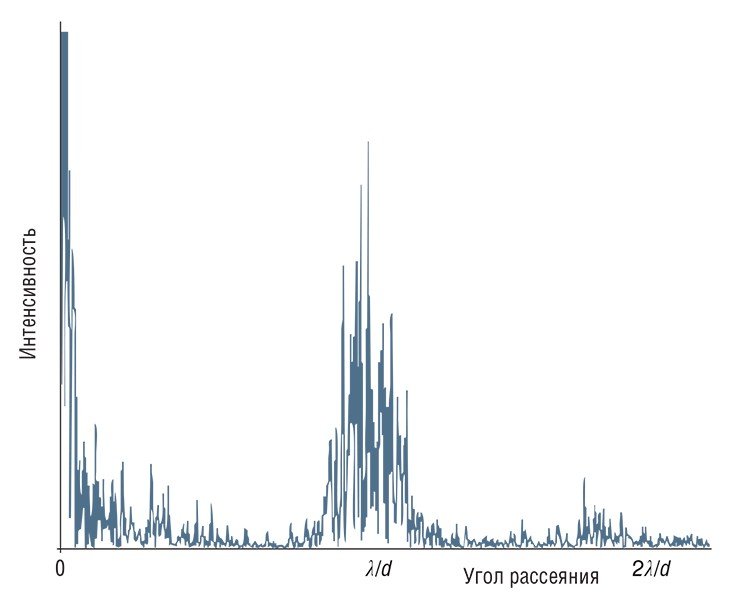
Таким образом, характерные особенности дифракционной картины, наблюдаемой в опытах с запотевшим стеклом, обуславливаются наличием ближнего порядка в расположении капель. В такой дифракционной картине обязательно имеется центральная темная область, в отличии от дифракции на случайно расположенных рассеивающих частицах.

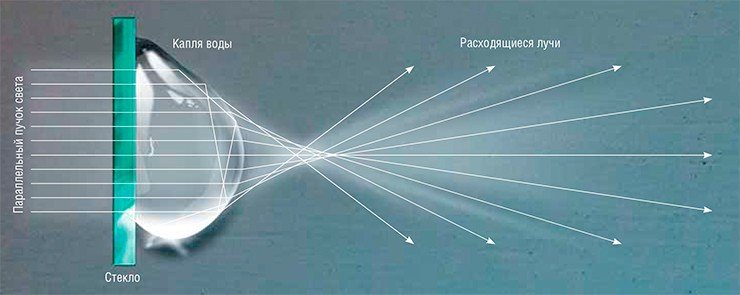
Надо сказать несколько слов о том, какую роль в исследуемом нами явлении играет прозрачность капель влаги на запотевшем стекле. Каждая капля — это собирающая линза. В приближении геометрической оптики такая линза превращает плоскопараллельный пучок света в световой конус, расходящийся за фокусом. Если линза является толстой и короткофокусной (а капли именно таковы), величина угла при вершине конуса будет велика в сравнении с относительно малыми углами дифракционного рассеяния. Поэтому такую линзу в нашей задаче вполне можно было заменить непрозрачным кружком, что мы и делали.

Литература

Cowley L., Laven P., Vollmer M. Rings around the sun and moon: coronae and diffraction // Physical Education. 2005. V. 40. P. 51—59.

Борн М., Вольф Э. Основы оптики. М.: Наука, 1973.

Китайгородский А. И. Рентгеноструктурный анализ мелкокристаллических и аморфных тел. М.: ГИТТЛ, 1952.

Миннарт М. Свет и цвет в природе. М.: Наука, 1969.

Авторы благодарят кинооператора С. Шуберта за техническую помощь в эксперименте с фотопленкой