IYPT-2013: «медовые кольца»
Совсем иная картина наблюдается, если воду заменить на достаточно вязкую жидкость, такую как мед, глицерин, шампунь или минеральное масло. Такая струя из-за высокой вязкости жидкости не успевает растечься, теряет устойчивость и начинает закручиваться в спираль. Это явление было предложено исследовать участникам Международного турнира юных физиков IYPT-2013 в задаче «Медовые кольца»
Исследователи, ранее изучавшие поведение струи вязкой жидкости при падении ее на горизонтальную поверхность, использовали силиконовое масло, инвертный сахарный сироп или полибутен (Mahadevan et al., 2000; Ribe et al., 2006). Во всех этих случаях вязкость жидкости была очень высока: примерно в 105 раз больше вязкости воды. В зависимости от условий наблюдалось несколько режимов образования колец: «вязкий», «гравитационный» и «инерционный».
 Наши основные эксперименты проводились с силиконовым маслом ПМС-10000, вязкость которого лишь в 104 раз больше вязкости воды. С десятикратным уменьшением вязкости связано важное различие в полученных нами результатах: оказалось, что в во всем доступном для наблюдений интервале скоростей реализуется только один режим образования колец, который заметно отличается от всех вышеперечисленных.
Наши основные эксперименты проводились с силиконовым маслом ПМС-10000, вязкость которого лишь в 104 раз больше вязкости воды. С десятикратным уменьшением вязкости связано важное различие в полученных нами результатах: оказалось, что в во всем доступном для наблюдений интервале скоростей реализуется только один режим образования колец, который заметно отличается от всех вышеперечисленных.
Первый этап – эксперимент
Наша экспериментальная установка представляла собой установленный на кронштейне открытый сверху сосуд, в который снизу была вставлена трубка с внутренним диаметром 4,5 мм. Вытекающая из сосуда вертикальная струя силиконового масла падала в нижнюю кювету, заполненную этой же жидкостью. Образующиеся при этом кольца снимали скоростной видеокамерой.
Высоту, на которой находился нижний обрез трубки над поверхностью масла в кювете, меняли в пределах от 0 до 20 см. Объемный расход жидкости во всех проведенных испытаниях составлял всего 0,06 см3/с, так что за время каждого испытания уровень жидкости в кювете и в сосуде оставался практически постоянным.
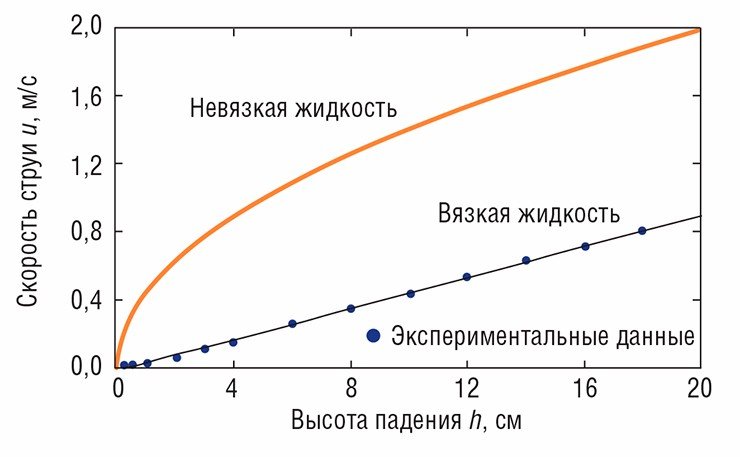
Определяющим параметром задачи является скорость, с которой струя налетает на поверхность. Чтобы узнать эту скорость, мы фотографировали струю, падающую с разной высоты, и измеряли ее диаметр. Затем, зная объемный расход жидкости Q и радиус струи a, рассчитали скорость u падающей струи по формуле u = Q/πa2 и проанализировали, как этот параметр меняется с высотой.
Эксперименты показали, что в интересующих нас пределах скорость струи растет пропорционально расстоянию от отверстия трубки. Это правило не работает на совсем маленьких (миллиметровых) расстояниях, но на этих высотах кольца на струе и не образуются. Линейная зависимость не будет работать и на больших расстояниях: ведь вязкая жидкость не может падать быстрее невязкой, а скорость падения невязкой жидкости растет с высотой по известному «корневому» закону свободного падения.
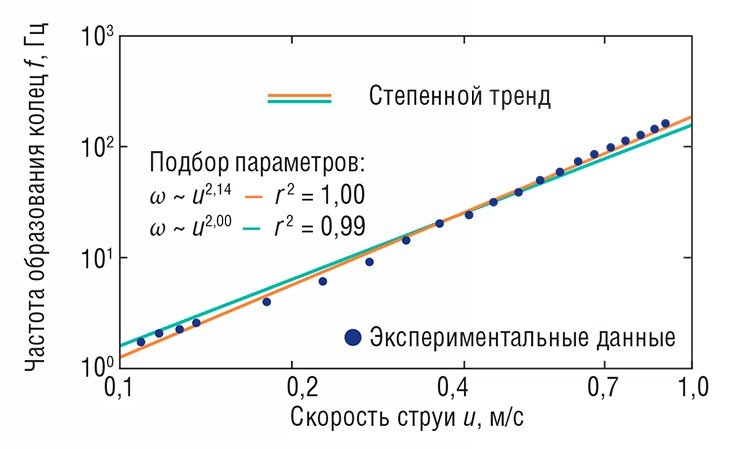
Чем больше скорость падения вязкой жидкости, тем с большей частотой закручиваются кольца и тем меньшие размеры они имеют. Оказалось, что полученную зависимость с хорошей степенью точности можно считать степенной с показателем степени 2,14. Теперь рискнем предположить, что в показателе степени должно стоять не дробное число, а целая двойка, и попробуем построить теоретическую модель, дающую такой скейлинг (степенную взаимозависимость двух величин).
Второй этап – теоретическая модель
Основная идея предложенной нами теоретической модели состоит в предположении, что вязкие силы, действующие в закручивающемся кольце, полностью гасят импульс струи до того, как она соприкоснется с подложкой.
Изложим ход наших рассуждений. Пусть струя вязкой жидкости на подлете к поверхности имеет радиус a и скорость u. Тогда объемный расход жидкости составит Q = S u = πa2u. Далее введем еще два параметра: радиус R и угловую частоту ω закручивающихся колец, которая будет равна ω = u/R.
Теперь запишем второй закон Ньютона для той части струи, которая укладывается в кольцо. «Вязкую силу» F, действующую на нижнюю часть струи со стороны подложки и направленную вертикально вверх, оценим как произведение динамической вязкости η, сечения струи S и градиента линейной скорости укладки кольца u/R = ω:
F ~ ηa2u/R ~ ηQ/R ~ ηQω/u.
Приравнивая эту силу к изменению импульса ρQu (ρ – плотность жидкости), получаем простое соотношение, связывающее частоту образования колец и скорость струи:
ω ~ ρu2/η.
Таким образом, в рамках наших теоретических предположений об укладке струи частота образования колец оказывается пропорциональна квадрату скорости струи. Эти теоретические выкладки хорошо согласуется с результатами нашего эксперимента.
Почему же при обработке экспериментальных данных мы получили столь странный дробный показатель степени? Ведь если при подборе параметров функциональной взаимосвязи экспериментальных величин принудительно задать целочисленное значение показателя степени, равное двум, то коэффициент корреляции между этими величинами останется очень близким к единице. Из этого следует, что квадратичная зависимость также является достаточно хорошим приближением.

Причина отклонения экспериментальной зависимости от квадратичного закона может быть связана, например, с погрешностями измерения малых значений толщины струи.
Кроме того, по мере укладки очередного кольца нижние под ним отчасти успевают расплываться, так что наложение кольца происходит, по сути, на наклонную поверхность. И сила, действующая при этом на укладывающуюся часть струи, направлена не строго вертикально. Наконец, свой вклад может вносить и влияние поверхностного натяжения жидкости. Возможность проверить эти и другие предположения предоставляются нашему любознательному читателю.
Литература
Barnes G., Woodcock R. Liquid rope-coil effect // Am. J. Phys. 1958. V. 26. P. 206—210.
Mahadevan L., Ryu W. S., Samuel A. D. T. Fluid rope trick investigated // Nature. 1998. V. 392. P. 140. Correction: 2000. V. 403. P. 502.
Ribe N. M. Coiling of viscous jets // Proc. R. Soc. Lond. A. 2004. V. 460. P. 3223—3239.
Ribe N. M., Huppert H. E., Hallworth M. A., et al. Multiple coexisting states of liquid rope coiling. // J. Fluid Mech. 2006. V. 555. P. 275—297.










