: 14 Dec 2013 , With cause all Russia fashions lays ABOUT BORODINO! , volume 36, N3

Some Elements of Quantum Informatics

The study of individual quantum systems, which became possible owing to the development and improvement of fine experimental methods, is a principally new and promising approach to the research of the nature. Experiments with individual ions and neutral atoms interacting with individual photons were awarded with the Nobel Prize in physics in 2012.

The quantum character of such objects is manifested as follows: these objects possess a discrete set of possible states, which can be “switched” by affecting them with electromagnetic radiation. Actually, they can act as a kind of logical elements, which can form a basis for creating a computational system.

Computing uncomputable

Why do we need quantum computers? It could seem that conventional computational systems are sufficiently powerful and the computation velocity can be increased by thousands of times owing to parallel computation methods.

Nevertheless, there are some problems that cannot be solved by the classical computers within reasonable times. First of all, these are all exact (nonempirical) quantum mechanics computations of atoms and molecules: if a molecule of interest for us contains N electrons, then the time necessary for sequential computations is proportional to a certain number raised to the power of N and becomes greater than the Universe existence period already for several dozens of electrons. These difficulties were discussed in 1981 by Richard Feynman in his lecture entitled “Simulating physics with computers.”

However, back in 1980, Yurii Manin in his pioneering publication entitled Computable and Uncomputable (Manin, 1980) put forward an idea of creating “quantum automata” for computing the process of unfolding of the DNA double helix: it was proposed to use a system possessing the quantum rather than classical properties for simulating quantum mechanics phenomena.

At the time when the papers of Manin and Feynman were published, the possibility of using quantum objects in computers was purely hypothetical. However, owing to the development of experimental methods, there appeared recent engineering prospects of creating computational systems that utilize the quantum properties of microscopic objects. Naturally, this idea arouses a tremendous interest of the scientific community.

It seems to be zero, but it is a little bit of unity as well

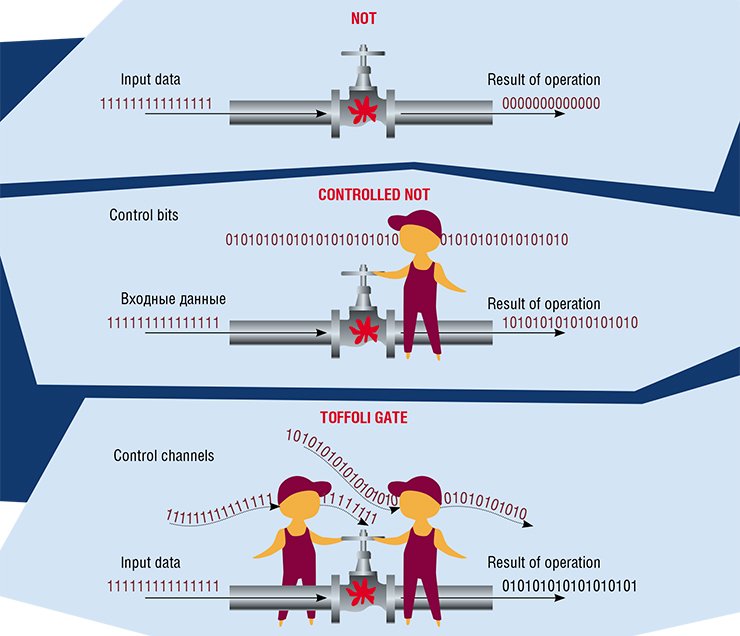
Usual computers perform mathematical operations over numbers presented in a binary form, i.e., as a sequence of zeroes and unities. The binary system is convenient from the viewpoint of hardware implementation: the memory cells where these numbers are stored should have only two states (yes/no): the voltage is or is not supplied, there is or there is no magnetization, etc. The binary computation process reduces to a sequence of operations over zeroes and unities or, actually, to changes in the states of the memory cells and registers containing the numbers in accordance with certain rules.

A quantum computer, like the classical computer, can be constructed on the basis of the binary calculus. Some microscopic objects displaying quantum properties possess two states, which can be used for encoding zeroes and unities.

For instance, it could be an atom possessing an intrinsic magnetic moment (spin). Being placed into a magnetic field, such an atom can have two orientations of the spin: along the field and opposite to the field.

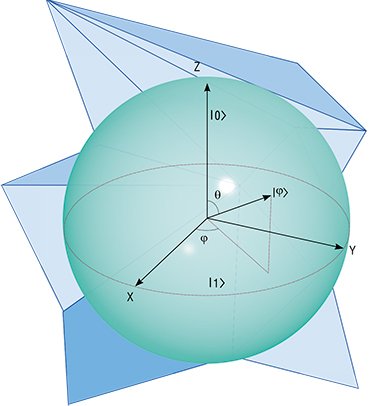
However, in contrast to the usual memory cell, which contains either a zero or a unity, the quantum object can be in a special state called a superposition. In this case, the measurement of the atom spin orientation in a magnetic field can yield both an upward-directed spin and a downward-directed spin. If such an object is used as a memory cell, the readout of information from this object will yield a zero with a certain probability or a unity with a certain probability.

Moreover, quantum memory cells, which are conventionally called qubits, can interact with each other and can be in a common (collective) quantum state. In this case, the state of several cells can be changed almost instantaneously by affecting only one of them. It is this collective behavior of interacting qubits (quantum register) that allows solving those computational problems that cannot be solved on usual computers.

The most important requirements to the quantum computer as a physical system are the possibility of controlling the state of each individual qubit and complete isolation from the ambient medium. The qubit is an atomic-scale object; for the qubit to remember its state for a sufficiently long time, it should be isolated from external actions or, in other words, its state should retain coherence. In any case, the time needed for quantum superpositions to fail should be large, at least, it should be greater than the time needed for one quantum logical operation to be performed by a factor of 10⁴.

For real computations, the qubits should be united into a quantum register. Individual qubits in the register should be discernable and controllable from outside. The qubits should have exactly two levels and should not pass spontaneously to a third level. Moreover, there should be a possibility of scaling the quantum register, i.e., adding new qubits if necessary. Interaction of qubits with each other should be controlled. It is the interaction of qubits, its form and characteristics that determine which logical operations can be performed by the quantum register.

The final state of the register should also be measured sufficiently rapidly. An important factor is the efficiency of this measurement: it is necessary to readout information from a microscopic object of an atomic size.

Photon qubits

Today, various physical systems are studied for the implementation of quantum computations (Ladd et al., 2010). For instance, the photon polarization direction, which is practically not prone to decoherence, can be used as the qubit states. Logical operations with the use of photons can be performed by using plates made of birefringent materials rotating the polarization of light. The main difficulty is to ensure interaction of individual photons, which requires optical media with extremely high nonlinearity. For this purpose, it is possible to use the effects of electromagnetically induced transparency or interaction of atoms with photons in a microwave cavity.

It was demonstrated in 2001 that quantum computations can be implemented on the basis of single-photon sources, as well as detectors and linear optical schemes with beam splitters and interfering single photons (Knill, 2001).

Information from photon qubits can be read out by using silicon single-photon detectors, which ensure a quantum efficiency of 70% at room temperature. The quantum efficiency of superconducting detectors can reach 95%, but they should be cooled down to 100 mK. The performance of superconducting detectors can be drastically increased by using nanowires.

However, the major drawback of quantum computational schemes based on polarization of photons is the high rate of photon losses, which is commensurable with the rate of decoherence in alternative implementations of the quantum computer.

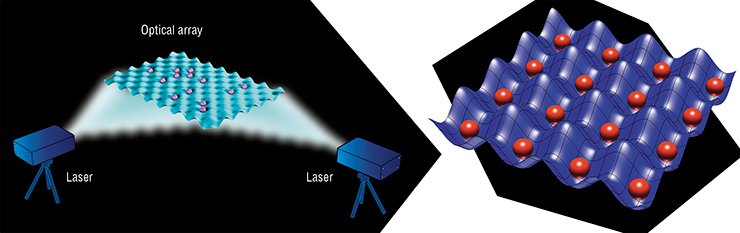
For writing quantum information, it is possible to use hyperfine states of neutral atoms whose lifetime is a few seconds. Long-range interactions between atoms allow two-qubit logical operations to be performed, and the accuracy of measuring the final state of the qubit is close to 100%.

For creating a quantum register, it is possible to trap neutral atoms into optical grids formed by standing light waves. The intersection of beams of two lasers generates a standing electromagnetic wave with atoms being attracted to the antinodes of this wave. Thus, spatially ordered structures can be formed from them.

In 2010, researchers from the University of Wisconsin-Madison (USA) managed to perform quantum logical operations with cold neutral atoms (Isenhower, 2010).

A similar approach is to use ions cooled down by laser radiation owing to resonant light pressure forces and confined by an electric field.

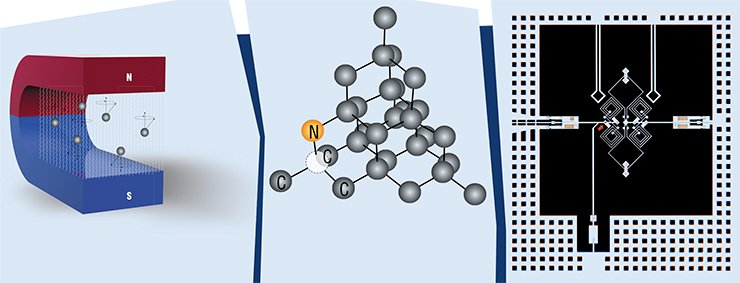
Quantum registers composed from several qubits were successfully implemented in molecules with the use of nuclear magnetic resonance (NMR). In a magnetic field, the nuclear spins start to precess and become aligned parallel or anti-parallel with respect to the magnetic field direction. These two possible directions correspond to logical states of qubits. In molecules, the precession frequency is different for different atoms. As a result, individual atoms in a molecule can be addressed by using resonant electromagnetic radiation. Simple quantum algorithms were demonstrated in quantum NMR computers on the basis of organic molecules, but scaling of such systems is still impossible.

Instead of arrays of neutral atoms confined by laser radiation, it is possible to use arrays of “artificial atoms,” e.g., quantum dots in semiconductors (Valiev, 2001). In this case, the logical states of the qubit are presented by two states of the electron spin in the quantum dot. For creating qubits, it is also possible to use donor atoms of phosphorus in semiconductors or nitrogen vacancies in diamonds. The spin states of such qubits are easily controlled by external electromagnetic fields, the lifetime of the spin state reaches several milliseconds, and spin-spin interactions allow obtaining coherent superpositions of the states and performing operations with two and more qubits.

A popular and fairly promising method of quantum computer implementation is the use of superconductors: in this case, individual qubits can have a mesoscopic character and contain up to ~10¹⁰ moving quantum-correlated electrons. The advantage of this approach is the large time of decoherence.

Many of these methods are now developed in particular, at the Rzhanov Institute of Semiconductor Physics of the Siberian Branch of the Russian Academy of Sciences, including the study of quantum dots, nitrogen vacancies in diamonds, and interaction of ultracold Rydberg atoms.

Quantum cryptography

The achievements in creating quantum logical elements make it possible to pass to the implementation of quantum informatics principles in practice. Though quantum computational systems potentially possess tremendous capabilities, they will not replace usual computers. Similarly, lasers did not make ordinary sources of light disappear, but provided a solution for new and specific problems.

For example, experiments in quantum optics made it possible to demonstrate fundamental physical phenomena, such as quantum entanglement: the measurement of the state of one quantum object may lead to a change in the state of another quantum object quantum-correlated with the first one. The quantum cryptography protocol described below does not require quantum entanglement: it is based on the impossibility of quantum state copying.

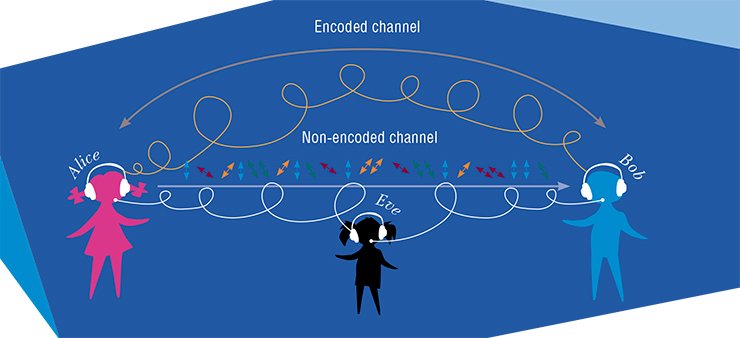
The transmitter (Alice) encodes information by setting this or that polarization of emitted photons, e.g., by transmitting them through the material that rotates the polarization plane. The vertical and horizontal polarizations mean “1” and “0,” respectively. The receiver (Bob) analyzes the received photon by a device that transmits only vertically polarized particles. Correspondingly, Bob receives “1” if the signal is captured and “0” if there is no signal.

Let Alice also transmit photons polarized in the diagonal direction: at an angle of 45 and 135° (in another basis). In this case, Bob captures the diagonally polarized photon by a vertically oriented analyzer and fails to obtain reliable values of zeroes and unities: there a certain probability of making a mistake, i.e., Bob receives “1” in 50% of cases and “0” in the other 50% of cases. To obtain reliable information, the receiver should know which type of polarization was used by the transmitter for encoding. This information is transferred by Alice to Bob through another (non-encoded) channel) by using this or that protocol.

If somebody tries to eavesdrop the data exchange channel (interceptor or Eve), she definitely does not know the basis. To remain unnoticed, Eve has to absorb the photon and emit the same light quantum back into the channel. However, she does not know which polarization basis was used (vertical or diagonal): she only received the signal “0” or “1.” Correspondingly, she cannot make an exact copy of the absorbed photon, thus, introducing an additional error into information received by Bob. Owing to this procedure, Alice and Bob notice that somebody tries to intercept their information.

Systems for secret data transfer on the basis of quantum cryptography methods are produced by ID Quantique and MagiQ Technologies. In addition, investigations in this field are performed in the interests of security agencies of some countries. Russian prototypes of quantum cryptography systems were created at the Rzhanov Institute of Semiconductor Physics.

References 

Isenhower L., Urban E., Zhang X. L., et al. // Phys. Rev. Let., 2010. V. 104.

Feynman R. P. Engineering and Science/ 1960. P. 22–36.http://www.nobelprize.org/nobel_prizes/physics/laureates/2012/

Feynman R. P. Simulating physics with computers // Int. J. Theor. Phys. 1982. V. 21. P. 467;

Feynman R. P. Quantum mechanical computers // Opt. News. 1985. V. 11. P. 11.

Knill E., Laflamme R., and Milburn G. J. // Nature. 2001. V. 409. P. 46–52.

Ladd T. D., Jelezko F., Laflamme R., et al. // Nature. 2010. V. 464. P. 45.

rabesinger A. (ed.) Nature Physics Insight // Quantum Simulation. 2012. V. 8. No 4.

Nielsen M. A., Chuang I. L. Quantum Computation and Quanum Information. Cambridge, UK: Cambridge University Press. 2010.

Vedral V., Plenio M. B. Basics of Quantum Computation, Progress in Quantum Electronics. Pergamon. 1998. V. 22. P. 1—39.

DiVincenzo D. P. Quantum computation // Science. 1995. V. 270. P. 255.

DiVincenzo D. P. The Physical Implementation of Quantum Computation // Fortschr. Phys. 2000. V. 48. P. 771.

Valiev K.A., Kokin A.A. Kvantovye komp’yutery: nadezhdy i real’nost’. Izhevsk: RKhD. 2001. 352 s.

Manin Yu. I. Vychislimoe i nevychislimoe. M.: Sov. radio, 1980. 128 s.

: 14 Dec 2013 , With cause all Russia fashions lays ABOUT BORODINO! , volume 36, N3