From Solid to Solid. Mechanics of Chemical Transformations

Academician V. V. Boldyrev, founder of the Siberian school of solid-state chemists, formulates three main constituents of this science in his first lecture on solid state chemistry (SSC) as follows: “defects + transfer processes + phase transformations.”

Using these concepts, it is possible to describe all SSC specific features and the area of its applications. Defects are arbitrary inhomogenities in an object; they are characteristic only of solids in contrast to liquids and gases. In solids migrating atoms have to “squeeze” through a densely packed network of atoms bonded to each other. Therefore, transfer of matter requires substantial energy consumption. As for phase transformations, these phenomena do not exist in gases or liquids. These three phenomena significantly affect the reactivity of solids.

As Russians say, “One cannot embrace the unembraceable.” Still, is it possible to single out one main specific feature of chemical reactions in solids? What is the foremost property that distinguishes “solids” from “non solids?”

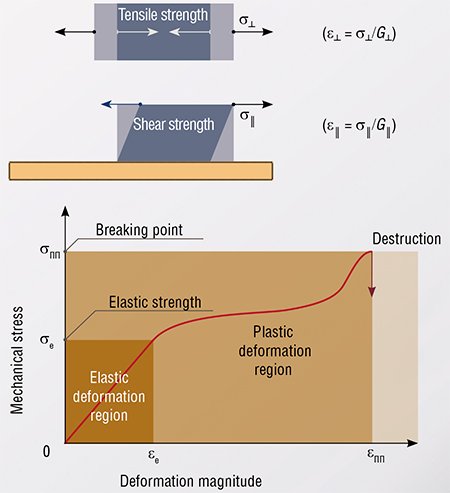
Of course, this is solidity. According to the high-school physics textbooks, it is the ability of solid bodies to retain their shape by resisting the action of deforming forces. The university physics calls this phenomenon existence of elastic properties.

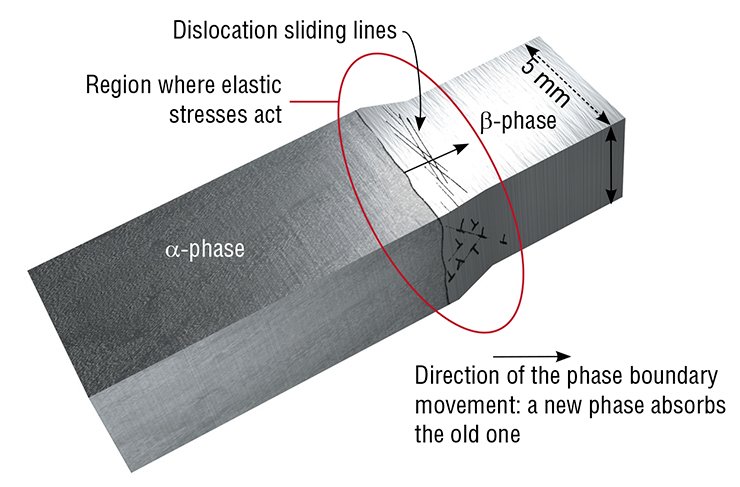
Beyond the elasticity limit

Any reaction of substances where at least one of the reactants and one of the products are solid and contact each other (we shall call such transformations solid state, SST) usually results in the change of the substance atomic structure accompanied by an increase or decrease of its volume. Expansion (or contraction) of the reacting material leads to the appearance of elastic mechanical stresses in the area of contact between the reacting substance and the newly formed substance. Obviously, the emerging stresses directly influence the reaction conditions by changing the local pressure. Furthermore, relaxation of these stresses generates defects in the crystalline structure, i.e. disruptions of the ordered structure, which, in turn, may also affect the conditions of the substance conversion.

Although no systematic experimental studies of the dynamics of elastic stresses during solid-phase transformations have been carried out, their relaxation has been extensively studied by a related field of science – solid state physics. Of course, physicists do not use a chemical reaction to create such stresses. Instead, they use physical methods, such as extension, compression, shear, non-uniform heating, etc.

DISLOCATION AS AN INSTRUMENT OF RECONSTRUCTION One of the simple models of a crystalline solid is an ideal crystal where atoms are arranged in strict order in all directions. However, “the world is not perfect .” The world of crystals is no exception to this rule: their perfection is disrupted by defects. There are three types of defects: surface defects such as crystal faces, grain boundaries, interface boundaries; linear defects (dislocations); and point defects (interstitial atoms, etc.).
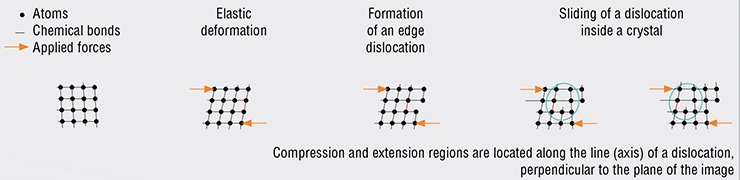
Plastic deformation of solids is caused by the movement of dislocations, which can be imagined as a broken edge of an atomic half-plane inside a crystal. The most efficient movement mechanism is dislocation sliding i.e. movement in the direction perpendicular to the half-plane. When a dislocation travels another interatomic distance, atoms adjoining the dislocation axis are subject to a collective shift.
As soon as the dislocation reaches the opposite face of the crystal, the stress is released; and the two faces of the crystal become “ideal” again. However, they are now shifted by one interatomic distance – a “step” is formed. This process results in the mass transfer of a large amount of substance because the dislocation axis penetrates the crystal all the way through. It is similar to turning over pages in a thick book: after the turning over is completed, the book will be located adjacently.
Another type of dislocation movement, climb, goes parallel to the broken atomic half-plane due to the one-by-one movement of atoms located on the dislocation line. In the end, atoms forming the excess half-plane go to vacancies or to the crystal surface, and the dislocation, as well as the stress, vanishes. Such a mechanism of mass transfer is called dislocation creep. Its implementation requires high diffusion mobility of atoms, which is reached at temperatures close to the melting point

So, what will happen if the stress applied to a body exceeds the elasticity limit of the material? This will lead to a plastic deformation of the body characterized by an irreversible shift of its one part relative to the other. Deformations of this type are caused by the movement of dislocations – linear crystal defects.

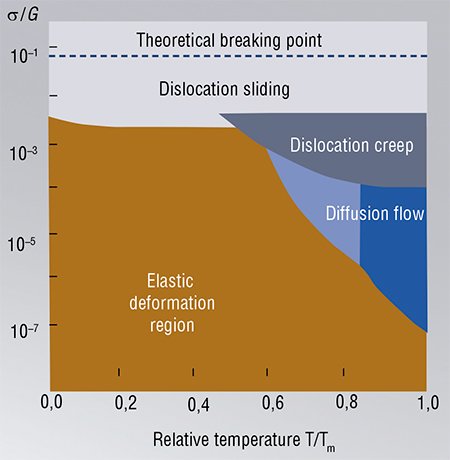Several types of dislocation movements are distinguished. The first one is sliding. It can be compared to the movement of a caterpillar, when it successively moves the parts of its body. Sliding of dislocations is characterized by the collective movement of atoms. This is different from other mechanisms of mass transfer such as creep, diffusion flow, which take place when the temperature approaches the melting point of the material.

It is interesting that mechanical properties of all solid materials have common features despite the variety of crystalline structures and types of bonds between atoms. Furthermore, regions corresponding to different types of deformations practically match for different substances in the diagrams built in the coordinates “temperature/melting temperature” vs. “mechanical stress/shear modulus.” This similarity allows one to predict the most probable mechanisms of stress relaxation under certain conditions.

Thus, internal mechanical stresses, which are generated during various solid-phase processes (phase transformations, chemical reactions of decomposition or exchange with participation of metals, ionic or ionic-covalent compounds), relax either by variants of plastic deformation, or by destruction, or by change of the shape.

For certain model transformations we managed to discover and describe quantitatively the mechanisms of how structural changes and stresses induced by them influence each other.

Self strain-hardening as a result of creep

Chemical reactions of solid substances include, at least, two stages: the chemical reaction proper, i.e. formation of a new substance, and structural stage, i.e. formation of a new solid phase. This complicates their investigation. Transformation of one chemical phase into another – polymorphous transformation of a substance without changing its chemical composition – can be analyzed as a model of the structural stage, not complicated by any “chemical specifics.”

The phase transformation in ammonium chloride β→α accompanied by a decrease of the substance density is a good model for investigation of the specific features of crystalline structure reconstruction. The transformation begins at 457 K (184°C) or at higher temperatures.

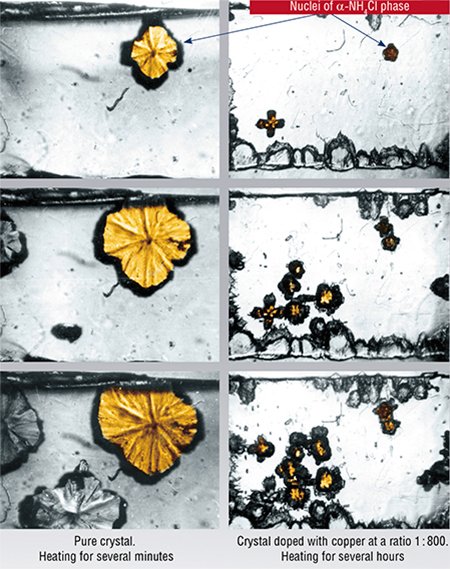The hydrostatic pressure created at the interface boundary by the nucleus of the α-phase estimated by the order of magnitude from the known shear modulus of β-NH₄Cl is about several thousand atmospheres. However, according to theNH₄Cl phase diagram, the minimum temperature necessary to begin the polymorphous transformation at such pressure has to exceed the actually observed value by hundreds of degrees.

In practice, phase transformation in thin lamellar β-NH₄Cl crystals occurs when crystals are overheated by just one degree. Such discrepancy is explained by the fact that the calculated pressure substantially exceeds the elasticity limit of this material. Relaxation of stresses takes place, the pressure decreases, and overheating becomes not necessary for the reaction to occur (Chupakhin et al., 1987). The ionic character of the crystal suggests that mechanical stresses caused by the volume increase are likely to relax via the dislocation sliding mechanism.

With time, the nuclei growth slows down until a complete stop. The deceleration results from the fact that dislocations form a thick “forest” where they start impeding each other’s movement. As a result, the stress relaxation by sliding becomes more and more difficult. Finally, the deformation mechanism changes to less efficient diffusion-dislocation creep (due to alternating diffusion of atoms along the dislocation axis). Essentially, this phenomenon is similar to strain-hardening (mechanical strengthening of a material due to plastic deformation). The only difference is that here it occurs due to internal rather than external forces. Therefore, it is called self strain-hardening (Sidelnikov et al., 1985).

SIZE MATTERS Doping is not the only method that is used to regulate the properties of materials. According to Saint-Venant’s principle the size of the region where elastic stresses act in a plate-shaped object is comparable with its thickness. Therefore, it is possible to affect the way in which stresses appearing in a solid relax by changing its geometry. The validity of this idea was demonstrated for the so-called tin plague, i. e. phase transformation of the metal white tin to the semiconductor grey tin that takes place at low (below 276 K) temperatures. (There is a hypothesis that tin buttons on the uniform of French soldiers disintegrated in severe frosts, which played an important role in Napoleon’s defeat in Russia. Indeed, it is hardly possible to wage war without buttons on pants…)
Common practice shows that a decrease of the particle size usually leads to an increase of their reactivity. However, the phase transformation of tin, produced an opposite effect: the transformation rate was found to decrease with the decrease of its thickness (Matvienko et al., 1997).
Why does it happen? The decrease of the sample thickness shortens the zone where stresses act and, consequently, the zone of plastic deformation. This was proven by visual observations. The size of the zone, where sliding lines are observed, decreases when the plate gets thinner. Since the number of dislocations generated per unit volume remains the same, in thin samples they have to “crowd” in a shorter zone, which increases their average density in front of the boundary. As a result, sliding of dislocations is hampered due to their intersecting and elastic interacting with the other dislocations. Hence, the movement rate of the phase boundary decreases as well

Alloying and doping

So, stresses forming during a solid-state transformation can substantially affect the transformation itself. The existence of such feedback allows one to regulate this process by changing purposefully the stress emergence and relaxation conditions. For example, one can hamper the dislocation sliding in the initial substance.

This approach is used in metal alloying, i. e. strengthening the metal by using special additives. For instance, iron is a relatively soft metal. This is why it is rarely used in pure form. However, addition of carbon and some other chemical elements in very small amounts substantially increase its hardness. The functioning mechanism of various alloying dopes can be different. Still, they frequently impede the sliding of dislocation in the metal, thus decreasing its elasticity and increasing hardness.

In the case of ionic crystals, ions with a different charge are efficient stoppers of the dislocation sliding. In particular, Cu²⁺ ions can be added to the above-mentioned ammonium salts. The experimental studies have shown that such doping (as alloying is called in “non-metal” chemistry) of NH₄Cl crystals actually impedes the dislocation sliding. Their path length becomes shorter, whereas the hardness of the crystal increases by an order of magnitude. Phase transformation of the crystal does not take place at the temperature typical of the pure substance; for it to occur the crystal should be overheated by tens of degrees.

Such changes occur even if only the subsurface layer of the crystal (no more than 10 μm deep) is doped. In this case the nuclei of the new phase appear only in the core of the crystal where the temperature at which the transformation starts is higher by 12—15 K than in pure undoped crystals. The doped surface layer, though, does not experience the transformation even after overheating by 70 K.

This is how changes in a mechanical property of a crystal, namely of its hardness, made it possible to increase the temperature of its phase transformation and alter its kinetics.

Glass metamorphosis

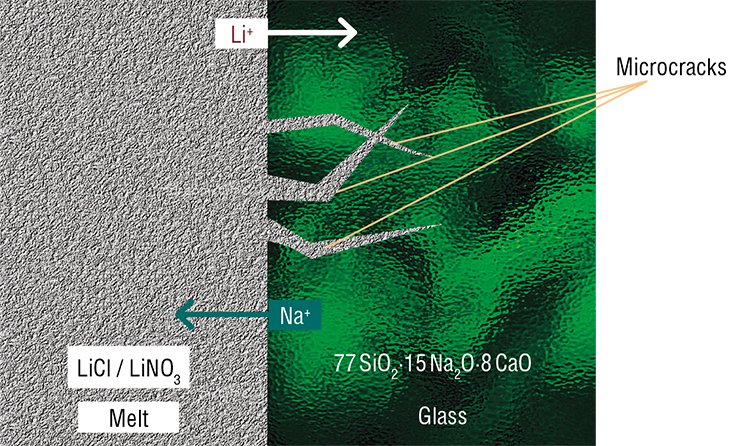
Phase transformations are an interesting and important subject that helps to understand how the “solid-state” world is arranged. Still, chemistry primarily deals with chemical reactions and the formation of new substances. The enormous effect of stresses on the kinetics of solid-state chemical transformations can be demonstrated with conventional glass where an ion-exchange reaction takes place.

The change of the volume after smaller lithium ions have substituted for sodium ions is not large – about 5 %. However, unlike crystalline ammonium chloride and tin, glass is an amorphous material. The orientation of chemical bonds and the lack of order in the location of ions make the formation of dislocations in it impossible. Hence, stresses must result in destruction. That is why glass is fragile!

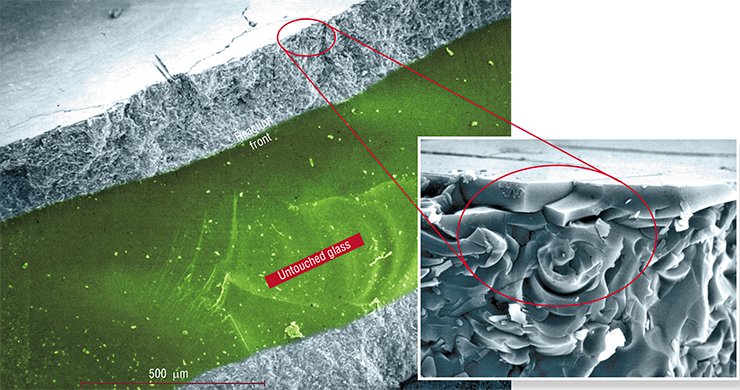
No wonder that glass substantially changes its appearance in the course of the reaction. After the reaction is completed, the material preserves its integrity but loses transparency, i.e. becomes opaque (Chizhik et al., 2007).

It is interesting to note that in this case the shape and typical size of the fragments resulted from destruction depend far more on the melt composition than on the reaction temperature.

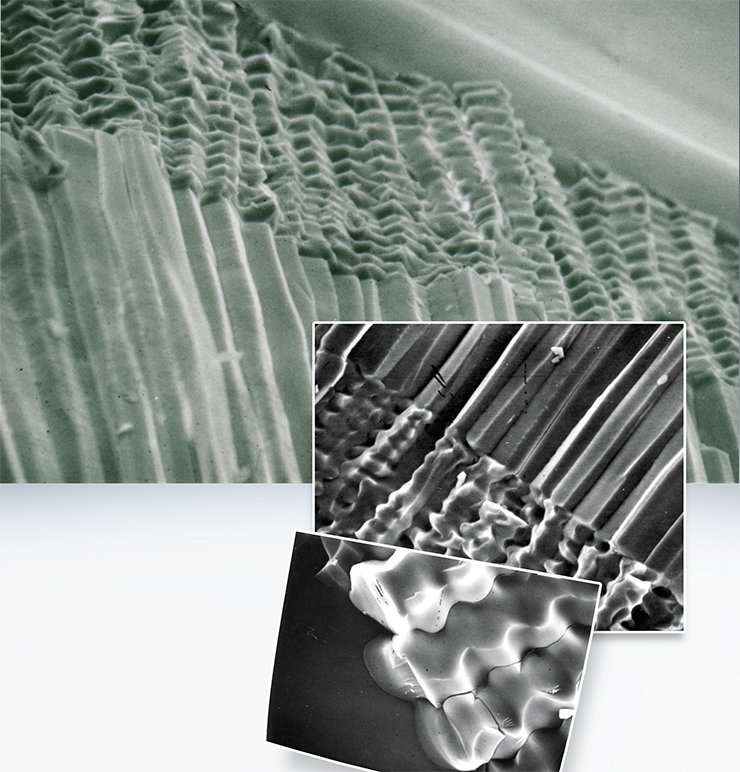
For instance, when glass reacts with a nitrate melt, fragments shaped as irregular platelets are chipped off. Glass reacting with a chloride melt, the cracks assemble into a network of almost regular hexagons. The movement of this network inside the glass, following the reaction front, results in the fragmentation of the glass into faceted columns (Chizhik et al., 2008).

The main reason for these differences is related to different phase diagrams of the systems “LiNO₃ – NaNO₃” and “LiCl – NaCl” or in other words, it is caused by the fact that the melting temperature of sodium chloride is significantly higher than that of nitrate. That is why solid inclusions are formed in chloride, rather than in nitrate, melts. The inclusions block the cracks used by the melt to reach the reaction zone. As a result, stresses in the reaction zone acquire a certain spatial configuration, in which cracks can steadily move only perpendicular to the front and get arranged into a regular hexagonal network. Stresses emerging during reaction in the nitrate melt do not allow the cracks to move so steadily – they constantly turn parallel to the reaction front.

These hypotheses were proven by an indirect experiment in mixed chloride-nitrate melts, which made it possible to realize intermediate modes between the ordered and the chaotic.

It should be noted that the phenomenon of spatial organization (self-organization) of a substance in physicochemical processes has been known for a long time. It includes hexagonal Benard cells formed by heating thin liquid films due to ordered convection; and Liesegang rings, which are a regular structure observed in products of some reactions. However, the formation of colonnades during ion exchange in glass, which that is initially an isotropic material, belongs to a new class of such processes.

Kuril Giant’s Causeway

Of course, it is funny and instructive to examine images of different types of cracking in chemically reacting glass. Still, is there any benefit to the national economy from such an occupation?

Actually, there is! A macrokinetic model was constructed on the basis of the concept of feedback between a chemical reaction and destruction of a solid. The most important parameter of this model is the characteristic that reflects the scale of minimum possible destruction. (Chizhik et al., 2007; 2008). This parameter appears as a result of the energy conservation law: work expended to form a new surface must be equal to the energy of mechanical stresses released during the formation of a crack (as in the above problem on the destruction of glass).

This model is applicable to describing of a wide range of thermal decomposition reactions АВ_s = А_s + В_g (e.g. dehydration of crystalline hydrates or hydroxides, conversion of carbonates to oxides, etc.). The solid-state product of such reactions A is generated as the so-called pseudomorphosis reproducing the shape of the initial crystal, which consists of separate fragments and contains voids.

The magnitude of mechanical stresses and, consequently, the size of fragments of the formed product are primarily determined by the magnitude of shrinkage, which is usually known. Despite the existing limitations, the model makes it possible to estimate the minimum possible fragmentation unit, i.e. to predict the size of fragments into which the crystal will be broken during the chemical reaction. This is important for predicting the properties of substances formed in such reactions (Sidelnikov, 2011).

And this is not all. This model appeared successful in describing the formation mechanism of a natural phenomenon many million years old. We are talking about one of natural wonders the “Giant’s Causeway” in Northern Ireland. This structure consists of basaltic columns reaching a meter in diameter and tens of meters in length. There are many similar colonnades in the world. There is even a special term for them: columnar joints. There also exist basaltic joints with chaotic cracks.

An adequate model that could quantitatively describe the formation of an ordered colonnade from a melt has not been developed yet, although there were many attempts to make it. If we use the above-described model of glass dispersion during ion exchange, heat dissipation will act as an analog of the diffusion of ions to the reaction front. Basalt solidification is accompanied by heat release. So, the more intense the heat dissipation, the faster the solidification front will move inside the melted basalt layer.

Mathematical equations used to describe diffusion and heat dissipation are similar. The specific volume of basalt is lower than that of its melt (as the volume of lithium glass is lower that that of the initial sodium glass). So, tensile stresses appear during solidification. The application of the model developed for describing the ion exchange in glass allowed us to predict the size of the basaltic columns and describe the kinetics of their growth depending on the conditions of heat dissipation during the lava solidification.

Chemistry of the 21st century favors a microscopic approach since chemical reactions are changes of the state of valence electrons. The studies of reactivity go into such “details” as specific features of femtosecond processes, positions of vibrational and rotational energy levels of molecules, etc. So, doesn’t it seem an anachronism to use a phenomenological approach where substances and reactions are distinguished not by their chemical nature but rather by purely macroscopic parameters, such as differences in specific volume, surface energy and other not chemical properties.

The progress in the theory of chemical kinetics in gases and liquids was supported by easy and direct control over the conditions of such reactions: it is always possible to set or measure temperature, pressure, and reactant concentrations in a reactor or reaction vessel. However, a solid-state reaction does not simply occur in a vessel; instead it takes place in the zone formed due to the reaction itself. It is this zone that is the “reactor” of a solid-state reaction, which exists as long as the reaction itself continues. Such structures are usually called dissipative structures. Their most interesting feature is the capacity for self-organization.

Before proceeding to describe the kinetics of solid-state reactions on a microscopic level, it is necessary to study the principles of self-organization in such a reactor. Naturally, the investigation of the reaction zone structure is hampered by its small size, usually of the order of nanometers, and by a multitude of interconnected physicochemical processes taking place in it. However, without this, it is impossible to develop the understanding of the mechanism of solid-state reactions.

References

Sidel’nikov A. A., Chupahin A. P., Boldyrev V. V. Vlijanie voznikajushhih pri tverdofaznyh prevrashhenijah mehanicheskih naprjazhenij na ih kinetiku. II. Regulirovanie temperatury polimorfnogo prevrashhenija NH4Cl gomofaznym i poverhnostnym uprochneniem // Izv. SO AN SSSR. Ser. him. nauk. 1985. № 17, vyp. 6. S. 39—49.

Chizhik S. A., Sidelnikov A. A. The kinetics of solid state reactions accompanied by fracture: I. Reaction of ion exchange in lime-soda glass; II. Model of stationary front with disordered fracture morphology; III. Model of stationary front with spatially ordered fracture morphology // Solid State Ionics. 2007. V. 178. P. 1344—1352; P. 1487—1492; 2008. V. 179. P. 1823—1834.

Chupakhin A. P., Sidel`nikov A. A., Boldyrev V. V. Control of the Reactivity of Solids by Changing their Mechanical Properties // Reactivity of Solids. 1987. V. 3, № 1. P. 1—19.

Matvienko A. A., Sidelnikov A. A. The influence of relaxation of stresses occurring during the β→α transformation of tin on the kinetics of the transformation // Solid State Ionics. 1997. V. 101—103. P. 641—646.

The photos used in the publication are the courtesy of authors and D. V. Kulakov