On the Way towards Personalized Medicine. Dynamic Modeling of Tumor Development
In one of the previous issues (SCIENCE First Hand №2 (38), 2011 (in Russian), # 2 (29), 2011 (in English)), the authors of the present paper introduced the readers to some of the problems and methods of personalization of drug therapy of cancer, one of the most complex problems in modern medicine. In this paper the authors present some achievements in oncogenic process modeling. Computer-based expert system developed within this modeling approach may in the nearest future become a valuable tool for oncologists helping to choose and optimize the individually selected patient treatment regimens
Today there are many different approaches to the modeling of tumor development resulting from the works of biochemists, system biologists, physicists and mathematicians. Unfortunately, despite the breadth and depth of the knowledge on the oncogenic processes at the cell and molecular levels, all the efforts made so far have not yielded an adequate model describing tumor development.
This is not surprising because even at the early stages of development, tumors contain millions of cells. If one attempts to describe tumor behavior starting from the cell level, using a few differential equations per each cell, none of the existing computers will be able to perform all the calculations needed to find a solution. Moreover, for the tumor development model to be useful, it must take into account the interaction of the tumor and of the applied drug. For example, adequate models must account for the drug action, drug concentration and drug excretion from the body, which in itself is quite complex. Also, they must account not only for the influence of the drug upon the tumor, but also for the influence of the tumor on the drug (for example, on its distribution in the tumor), which today is not done even in the most complex modeling systems.
But if the above “bottom up” approach – starting from the knowledge of details and moving towards more general features – is inadequate, may the “top down” approaches be will more helpful? The answer to this question is “Yes, they are.” For example, within the so-called phenomenological approach one starts from the well-known and experimentally proven general facts and relations, and moves deeper towards an understanding of more particular interrelations. Also, it is much more productive to start from a known mathematical model of some similar and already familiar phenomenon, and then to develop it further. Strangely enough, in the modeling of tumor development one can start from the model of the familiar phase transition “water-ice.”
This analogy is not superficial. It is well known that both water and ice are quite stable within corresponding temperature ranges, but near 0°C the properties of this system may change dramatically. Near the transition temperature, both phases – solid and liquid – having very different properties (for example apparent density) co-exist easily. Also the transition is reversible: cooling the water turns it into solid ice, and heating the ice turns it back into liquid water. Properties of this phase transition depend not only on the internal properties of the system, for example, the salinity of the water, but on the external ones such as atmospheric pressure.
One may wonder if it is feasible to speak about the “phase transition” in the system “normal tissue – tumor”? Oncologists are well aware of tumor stability – it is quite difficult to get rid of. At the same time, the normal “healthy” state of the tissue is also quite stable; our body is capable of combating almost everything that tries to shift this balance towards the “disease” state. A developed tumor has quite different properties as compared to healthy tissue, though it is originating from this same tissue, and is often co-existing with it for quite some time. Also, at certain conditions, for example, under successful treatment, tumors may regress and disappear (“melt”).
Of course one cannot directly use the models of phase transitions developed for non-living matter for the modeling of live matter. Nevertheless, modern science has already developed certain ways of applying models coming from mathematical physics to living systems. Here, prominent results have been achieved, for example, by the Italian school headed by Professor N. Bellomo, who has developed the kinetic theory of active particles (Bellomo et al., 2009; Bellomo, 2010).
Based on the results achieved by the Italian school and generalized theory of the phase transitions, the authors of the present paper have developed a concise mathematical model of tumor development (Mamontov, et al., 2006). It took four more years to connect all the formal parameters used in the model to the ones possible to measure experimentally.
On five postulates
The resulting mathematical model of tumor development is based on a very limited number of postulates.
• The tumor is a result of malfunctioning of natural regulatory processes. If the balance between the number of “born” and dying cells is disrupted, it means that the cell division process got out of control. If this control is lost completely, it leads to the growth of a tumor. And when the control is lost, the body cannot deal with the “malfunction” without external help. If proper treatment helps the internal regulation mechanisms, full control may be restored and the tumor will “disappear.”
• Solid tumors grow from so-called inflammatory infiltrates. It is known and experimentally proven that the inflammatory process is a part of the body’s “defense system,” but if this process goes beyond a certain threshold, it becomes dangerous.
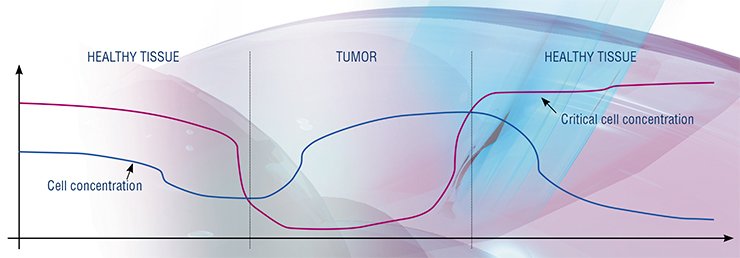
• Dynamics of the tumor development can be mathematically expressed using a single parameter, the cell concentration (number of cells in the unit volume). The following statements can be used for developing the corresponding equation systems. Firstly, both states, tumor and normal tissue, are asymptotically stable. Secondly, the mechanisms keeping the balance of cell numbers are biochemical and depend on the transport of certain “signaling molecules” towards the cells. (The last statement is not entirely correct for the tumors with developed blood vessel networks.) Thirdly, each tissue cell can follow either a “normal life” or an “uncontrolled division” pathway (mathematically we speak about the probability of choosing one or another path).
• For each space-point in our body, at each specific moment of time, there exists a “critical concentration” of cells, above which our regulatory systems cannot sustain the balance between the dividing and dying cells. If the cell concentration at this space-point is not decreased (for example by using therapy and killing some of them), or the critical concentration threshold itself is not shifted, cell division in the vicinity of this point will progress and a tumor will be formed.
• Therapeutic drug concentration in the tissue together with its space distribution and changes in time, are unbreakably coupled to the tumor dynamics in space and time. A good (adequate) model must take this into account. Unfortunately, all existing pharmacokinetic and pharmacodynamic models are not capable of doing this because of their origin (the first class models describe what the body does to the drug, and the second class models describe what the drug is doing to the body).
The above postulates have a very solid scientific foundation; so far, the authors have not found a single experimental fact contradicting them. Of course one should not forget that any model is limited and only approximates the reality within the boundaries of its applicability. For example, one of the already mentioned limitations is that such a model is hardly applicable to the tumors at late stages of development, when they have a developed blood vessel system.
When control is lost
Based on the above postulates, one can make a good model qualitatively describing the process of tumor development.
The cells in our tissue are not “floating free,” but are surrounded by a collagen matrix “scaffolding” and interstitial fluid filling all the volume. All life of the cells is governed by internal processes and external “controls” through “signaling” molecules, which are delivered to the cells from outside. These signaling molecules are moving in the interstitial fluid quite slowly; this motion is mainly controlled by diffusion. The therapeutic drugs, even when they are applied as injections or infusions, are moving with the blood flow only inside the blood vessels. After passing through the blood vessel walls their delivery is also diffusion-controlled.
If the cell concentration in the tissue is not too high, there is enough space occupied by the interstitial fluid, and the delivery of chemicals (including the signaling molecules) to the cells is efficient. The mechanisms of cell population control are also efficient. If in some place, at some point of time, the cell concentration increases, the volume occupied by the interstitial fluid becomes smaller and the efficiency of the chemical delivery mechanism decreases. Correspondingly, the regulatory systems must increase the number of produced signaling molecules to keep the proper number of them reaching the destination.
But each regulatory mechanism has its own limits, which may be, for example, determined by the “production rate” of the “factory” producing signaling molecules. Also this regulation is rather slow, as it is controlled by diffusion. Thus, at certain cell concentrations, the mechanism sustaining the cell number balance fails: the number of signaling molecules reaching the cells becomes inadequate and regulatory systems fail to prevent uncontrollable division of the cells. As a result, cell concentration at this point, and within its vicinity, continues to grow. With time this process can lead to another stable state, a solid tumor.
In the area where the concentration balance control is ineffective or is completely lost, the cell concentration is non-uniform. At the periphery of this zone, cell concentration is lower than in the middle, where control over the cell division was lost much earlier. But because control over the situation has already been lost, the dimensions of this zone increase, e.g. the tumor grows in size and simultaneously becomes denser in the middle.
When a therapy drug is injected into the bloodstream, it will work effectively only on the periphery of the tumor, because of the problems with its delivery to the areas with high cell concentrations. If, with the help of the drug, control over cell concentration on the periphery of the zone is restored and cell concentration becomes normal, the delivery of the drug and signaling molecules to the inner parts of the zone will also be improved. And as the cell concentration at the periphery of the zone falls below critical, drug therapy will slowly restore the proper cell concentration (and thus proper operation of natural control mechanisms) over the whole tissue, and the tumor will disappear.
Single equation
From the very beginning, authors have set the task to develop a “minimalistic” model, which would be capable of describing tumor development (including the case of drug therapy) still using a bare minimum of the parameters and relations absolutely necessary for the correct description of the phenomenon.
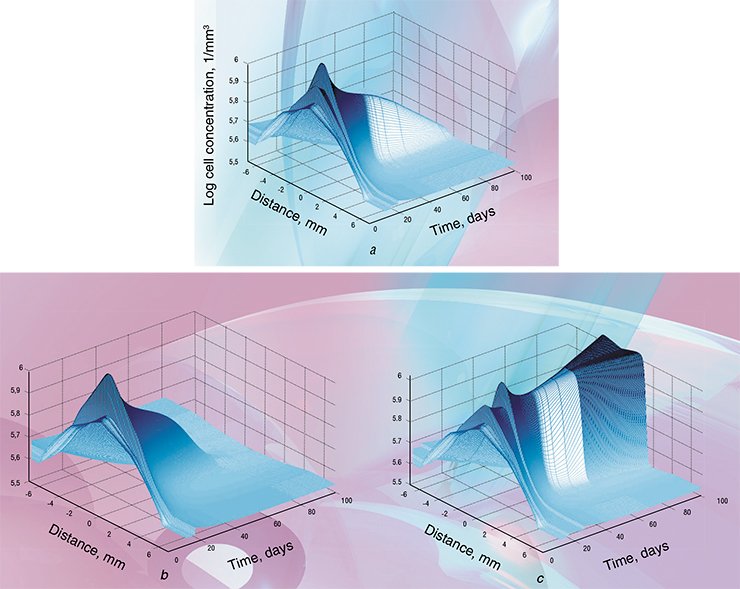
As a result of such minimization, a single (!) reaction-diffusion equation for cell concentration was left. This equation has only six major parameters: critical concentration (describing the threshold above which the internal cell concentration control mechanism fails), native cell concentration (the natural cell concentration kept by the regulatory mechanisms in the particular tissue), a diffusion coefficient, the cell cycle stage duration times and the cell death rate. Such equations are quite easily solved with the help of modern, and not even most powerful, computers.
The computer-based expert system PhasTraM (from Maintenance of the cell concentrations via Phase Transitions) allows for the individual optimization of the therapy regimens based on the results of clinical analysis. The program generates an individualized forecast of tumor development with or without the chosen therapy. If the forecast predicts that the tumor is not eradicated, adjustments of the therapy regimen can be continued.
Without any doubt, such programs cannot substitute a human being, and the decision on the particular therapy modality and regimen must be taken by a qualified specialist. But the main advantage of such systems is in the possibility of fast in silico assessment of multiple regimens resulting in a suggested optimized strategy. This assessment is carried out for the “virtual patient” without any risk for the real patient.
In the tumor initiation scenario discussed above, the process is triggered by cell concentration becoming higher than the “critical” value. On the one hand this can happen when the cell concentration is actually growing, for example because of the chronic inflammation process. On the other hand, even with a stable cell concentration, the same situation will occur if in some space-point the mechanism responsible for the maintenance of cell concentrations malfunctions. In terms of the model parameters, this means that the “critical concentration” value decreases significantly. This can happen, for example, with the lowering of general immunity, due to chronic stress, or when poisons or carcinogenic chemicals are getting into the body.
Interestingly, the present model can explain seemingly spontaneous tumor eradication cases. Although control over cell concentration was lost in some places of the human body, it does not necessarily mean that the corresponding natural regulation and control systems were “switched off” only that they became inefficient. And thus, everything that helps to increase the efficiency of our regulatory systems can help. So in some cases boosting our general immunity can actually help our body to eradicate the tumor. One can hardly expect this happening for every tumor, but boosting the immunity and raising a patient’s state of mind definitely help traditional tumor therapy.
How does it work?
Parameters needed for the operation of the PhasTraM expert system are split into two groups: the individual patient and tumor data, and the ones controlling the modeling process.
The first group is comprised of traditional patient data (weight, height, body temperature) and the results from the multi-pass biopsy test on the tumor. To get the information on the spatial parameters of the tumor tissue, samples are taken in a few spatial points inside the tumor and in the healthy tissue outside it.

Although multi-pass biopsy is more complex than an ordinary one, it yields a rather low rate of complications (even in case of such “delicate” organ as the liver). It should be noted here that the current version of the program only deals with spherically symmetric tumors. This restriction is practical and is not related to the modeling approach as such. To realistically model asymmetric tumors one needs the data of at least three multi-pass biopsies carried out in the orthogonal directions across the tumor. This would unnecessarily complicate the extraction of initial parameters, and undoubtedly increase the risks for the patient.
For each of the tissue samples, average cell concentrations, fractions of the volume occupied by the extracellular matrix and interstitial fluid, dynamic tissue viscosity and cell cycle duration times must be determined. These parameters are not extracted for the traditional biopsy, but the methods of their extraction are affordable and well known. There is only a problem with the dynamic viscosity of the tissue, which cannot be measured using traditional viscometers. This problem can be bypassed by calculating the viscosity from the diffusion coefficients (though it is not a direct measurement and introduces additional errors). For example, by using MRI tomography it is possible to non-invasively measure the diffusion coefficients of water molecules in the tissue with high spatial resolution (Schepkina et al., 2006). Gathered data can be used to calculate the tissue viscosity in each spatial point.
The second group of parameters includes (for the regimens with intravenous drug infusions): the name of the drug from the built-in library, dose, as well as the number and duration of the infusions. A similar list of parameters is used for the other forms of drug application, like peroral ones. Unfortunately modeling of drug action in peroral cases is much more complex because it must take into account everything that happens with the drug before it gets into the bloodstream.
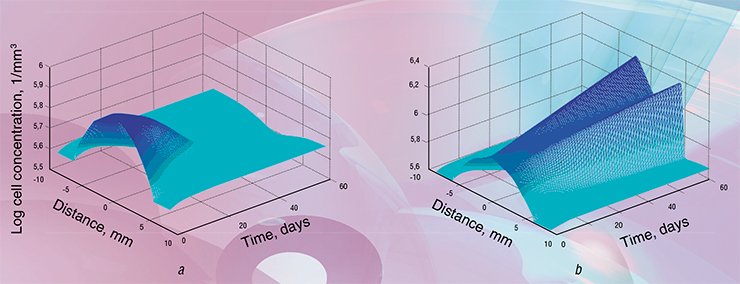
One of the known biomarkers of the chronic stress is Interleykin 6 (IL-6), protein molecules involved in the immune response reactions of our body. Experiments show that IL-6 concentration is elevating during the chronic stress. Elevated levels of IL-6 in the tumors are also confirmed by the results of histopathological tests.
Today it is assumed that hyperplastic lesions, one of the early stages of tumor development, are evolving from the chronic inflammations with the elevated levels of IL-6, which can be caused, in particular, by the chronic stress. Moreover, the presence of elevated levels of IL-6 in the tissue indicates that at least one of the autocrine signaling and regulatory mechanisms is malfunctioning.
Modeling of the tumor evolution for different IL-6 concentrations in the tissue has shown that with the normal IL-6 levels natural regulatory systems can successfully suppress and eradicate tumors at early stages of their development. But with the elevated IL-6 levels tumor growth is dramatically fast. Thus PhasTraM modeling supports the conclusion of the chronic stress influence upon the evolution of the tumors
For each of the drugs, the program must contain a separate module, describing its action in detail. It appears that, for the purpose of therapy individualization, one should select the drug by the trade name rather than by an active substance. It may seem strange, but in many cases the stated active substance is not the only one present in the drug, and also the active substance name in many cases is not equivalent to an exact chemical formula. An additional problem is the wide presence of so-called generic drugs, non-patented analogs of the original preparation. Such drugs in many cases are just bio-equivalent to the original ones, which means that they only have a statistically similar way of action (Le Corre, 2010). And statistical averaging appears to be one of the worst enemies of the treatment individualization.
Today, our expert system can make forecasts of tumor treatments with the cytotoxic drugs, for example radio-nuclide and chemotherapeutic ones. Recent modules allow for non-cytotoxic drugs, like monoclonal antibody-based ones and tyrosine kinase inhibitors. Another new module allows for the monitoring of the levels of some “signaling” molecules, like Interleykin 6. PhasTraM modeling approach also provides the possibility of individualizing radiation beam and photodynamic therapies, but corresponding modules have not yet been finalized.
Now all the initial parameters are loaded. After pressing “start” it takes about one minute or less to get the result (even when running on a relatively simple notebook computer). By the operator’s choice, the computer screen will present a set of graphs or surfaces illustrating the evolution of the tumor in space and time for the chosen therapy regimen.
For example, with the radionuclide therapy, the whole dose is often divided among a few infusions to decrease the adverse effects. Such fractionation, even in case of only two infusions has a very large number of options (different dose, different infusion time and infusion duration for each of two infusions). The selection task in the case of multiple small doses (for example to provide even “softer” regimens) is infinitely more complicated.
Without computer support, specialists often select equal doses in the fractions and equal intervals between infusions (varying infusion times is commonly not considered at all). With the help of a modeling program it is possible to vary all parameters of the fractionated regimen quickly assessing the forecasted result of the treatment. The task of parameter variation can also be delegated to the optimizing algorithm. Depending on the optimization task, the computer can suggest the regimens, which, for example, minimize the overall dose of the drug or treatment time, still achieving tumor eradication.
Many years of research and development have produced a mathematical model adequately describing tumor evolution in space and time. This model qualitatively agrees with all experimental data known. Early results of the quantitative comparison of model forecasts with the data from archives of Sahlgrenska Research Hospital (Göteborg, Sweden) and experiments conducted by the authors are also promising. Further laboratory animal experiments testing individualized modeling results with no statistical averaging of either input or output data are currently carried out with the help of the researchers from the Tyumen Branch of the Russian Academy of Sciences.
A careful choice of a small number of experimentally extracted input parameters has appeared to be extremely valuable: a research model has turned into an expert system for practical individualization of the tumor drug therapy regimens. It significantly simplifies the input data collection, reduces the cost of related analysis and the computation times. Today the work is focused on adding modules for new drugs into the system, modifying it for different operational systems and the development of a simplified version of the system for educational purposes.
One of the future versions of the system targeting the process of new cancer drug development will be able to assess the action of virtual drugs on virtual patients. The authors are hoping to present some of these systems to practical oncologists in the near future.
References
Basso A. M., Depiante-Depaoli M., and Molina V. A. Chronic variable stress facilitates tumoral growth: reversal by imipramine administration // Life Sciences. 1992. Vol. 50. P. 1789—1796.
Corre P. Le. Bio-équivalence et génériques de principes actifs à marge thérapeutique étroite (Narrow therapeutic index drugs: bioequivalence and generics) // Presse Medicale. Feb 2010. Vol. 39. No. 2. P. 169—176.
Koptioug A., Mamontov E., Myrberg T., Sukhovey Yu. Software for pretherapeutic design of tumor/patient-individual tumor-eradicating drug regimens // Communications in Applied and Industrial Mathematics. 2012 (in print).
Mamontov E., Koptioug A., and Psiuk-Maksymowicz K. The minimal, phase-transition model for the cell-number maintenance by the hyperplasia-extended homeorhesis // Acta Biotheoretica. 2006. Vol. 54. P. 61—101.
Schepkina V. D., Chenevert T. L., Kuszpit K., Lee K. C. et al. Sodium and proton diffusion MRI as biomarkers for early therapeutic response in subcutaneous tumors // Magnetic Resonance Imaging. 2006. Vol. 24. P. 273—278.