Future of Science: Discoveries – Expected and Unexpectable

The idea about the fundamental unpredictability of scientific discovery flourishes abundantly in the numerous articles and books on the essence of scientific creativity, with its roots going deep into the seemingly irrefutable experience of the many generations of scientists. How could Galileo have envisaged, when he was pointing his spyglass at the sky, that he would see mountains on the Moon and four satellites of Jupiter? How could Becquerel have foreseen what his forgetfulness would lead to when he accidentally left an undeveloped photographic plate next to radium salts? How could Mendel have known in advance the consequences of his experiments with peas? The answer seems obvious: no one of them could have known anything in advance since science moves forward by unbeaten tracks. This is why it is so fascinating to engage in science – ​you never know what discovery awaits around the bend…

There is a reason for this answer, but it only partly describes the real state of affairs. There are (still!) discoveries that are impossible, or at least extremely difficult, to predict. Let us call them discoveries of the first class. These include, for example, the above-­mentioned discovery by Becquerel of the radioactivity phenomenon.

DISCOVERIES OF THE 1ST CLASS are impossible to foresee. Examples include the discovery of electricity by Luigi Galvani, radioactivity by Henri Becquerel, the constancy of the speed of light by Albert Michelson and Edward Morley, accelerated expansion of the Universe by Saul Perlmutter, Brian Schmidt, and Adam Rees

Until the end of the 19th century, physicists rest assured that light, whether it be particles or waves (there had been an ongoing debate on this subject since the time of Newton and Huygens), conformed to the laws of physics, and specifically to the law of addition of speeds. However, the 1881 experiment by the US physicist Albert Michelson revealed no difference in the speed of light in different directions. That result proved to be unpredictable. The speed of light did not obey the law of addition of speeds. This, too, was a discovery of the first class.

There are discoveries one could have foreseen. They came unpredicted, however, because scientists had not taken the pain to scrutinize the research field in its entirety. Let us call them discoveries of the second class. One such example is the discovery of pulsars in 1967 by Jocelyn Bell, back then a 24‑year-old postgraduate student. Bell’s discovery came unexpected for many astrophysicists, but it was, nevertheless, quite predictable. The theory of neutron stars had been in place for three decades, and the fact that stars rotate, possess magnetic fields and are, therefore, capable of emitting narrow streams of particles could have been imagined without much effort (this is why scientists soon came up with a correct hypothesis about the nature of pulsars).

DISCOVERIES OF THE 2ND CLASS can be predicted. Examples are the discovery of X-rays, wave–particle duality, DNA structure, pulsars, and black holes

In the year of the discovery of pulsars, without knowing anything about them yet, we published an article together with Oktai Guseinov, the supervisor of my diploma thesis, on the capture of interstellar matter by a rotating magnetic neutron star. We wrote that the X-ray emission from such a star had to be periodic, with the period of emission being equal to the period of rotation. In fact, we predicted the existence of X-ray pulsars, which were discovered three years after our publication. That discovery also came unexpected for astrophysicists.

Discoveries of the third class are those predicted, but whose ultimate results could be different, to some extent, from the expectations.

DISCOVERIES OF THE 3RD CLASS were partly predicted. These include the discoveries made during the landing of Huygens on Titan; the discovery of dark matter by Fritz Zwicky and of dark energy by Albert Einstein; the discovery of a new planet in the Solar System by Michael Brown and Konstantin Batygin and the discoveries of exoplanets in multiple star systems

These are, for example, the discoveries made during the landing of the Huygens space probe on Titan, a satellite of Saturn. Scientists had expected its atmosphere to be dense and saturated with methane, hadn’t they? Of course, they had – ​and they had taken it into account when designing the spacecraft and calibrating the instruments. They could have expected methane rivers to flow across Titan’s surface, couldn’t they? Of course, they could – ​and they avoided talking about them before the mission not because they could not foresee them but because they did not want to be accused of having too wild an imagination.

Another example is the discovery of dark matter. In the 1930s, the US astrophysicist Fritz Zwicky (I will talk more about him later) stumbled upon a bizarre fact – ​some galaxies were rotating faster than they should have if their masses had been determined correctly (the masses were calculated from the luminosities, taking into account the distances to the galaxies). The galaxies turned out to be more massive than they were supposed to – ​as if they possessed some extra invisible mass. The scientific community was skeptical about Zwicky’s paper and considered his result to be an observational error. In the 1970s, US astronomers published several more papers on this subject, but they went unnoticed. Only two decades later, the problem of invisible dark mass became generally recognized, when it came to determining the mass of the entire visible Universe rather than individual galaxies

Finally, there are the fourth-­class discoveries, which are exactly as predicted. These discoveries emerge as corollaries from a theory proposed by someone to explain a previously discovered phenomenon.

DISCOVERIES OF THE THIRD CLASS: DARK ENERGY In 1917, Einstein was analyzing his own gravity equations to discover that they had no stationary solutions in the case of the Universe. The Universe must either be expanding or contracting. However, Einstein trusted “facts” more than equations. Back then, scientists did not yet know about the expansion of galaxies, and the galaxies themselves were regarded as gas clusters. Moreover, the attitude of physicists to mathematics has changed noticeably since those days. In order to obtain stationary solutions, Einstein introduced a linear term into his equations, which he called the cosmological constant.
If we introduce such a constant into the equation, we indeed obtain a stationary solution of the gravity equations for the Universe. In the physical sense, this constant meant the existence of some kind of pressure that acted against the forces of gravity. However, in 1922, the Soviet mathematician Alexander Fridman also solved these equations and published an article where mathematics was considered superior to “facts”. Fridman argued that the Universe must indeed be expanding. Einstein did not agree with the article, but in the late 1920s, the American scientist Edwin Hubble discovered the recession of galaxies and determined the approximate age of the Universe.

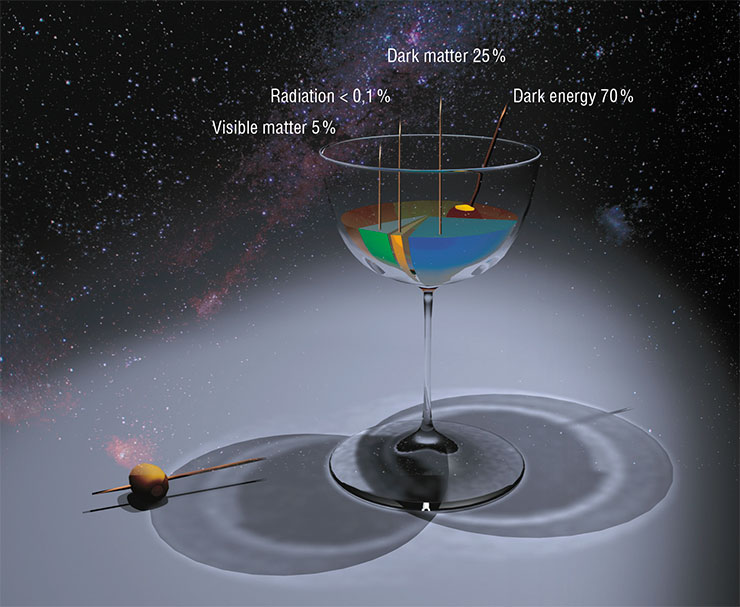
Hubble’s discovery came as a surprise to astrophysicists although it had actually been predicted a decade earlier. Einstein abandoned the cosmological constant, and since then the equations had long been solved without it. By the 1990s, scientists had been regarding the cosmological constant as a curiosity. But right at that time, it was discovered that the Universe was not merely expanding – it was doing so at an accelerated rate, contrary to Einstein’s equations. This is why scientists had to introduce some kind of energy that pushes the Universe apart. In fact, this is the return of that same cosmological constant

Speaking about the aforementioned discovery of pulsars, when the first theoretical works appeared on the physics of their radiation, it was easy to predict the discovery of neutron stars emitting in the optical and X-ray ranges. Both optical and X-ray pulsars were discovered several years later, which fully confirmed the conclusions of the theorists.

In 1965, Penzias and Wilson accidentally discovered background microwave radiation, thus proving that the Universe emerged in the Big Bang. In 1978, they received the Nobel Prize although they had only corroborated the result published by Gamow, Alpher, and Herman back in 1948.

DISCOVERIES OF THE THIRD CLASS: PLUTO AND THE MAJESTIC POWER OF FORTUITY The history of the discovery of Pluto began when Urbain Le Verrier had discovered Neptune with “the point of his pen,” as François Arago, the director of the Paris Observatory, aptly said. The Frenchman Le Verrier and, independently of him, the Englishman John Couch Adams calculated the celestial position of a planet whose gravity perturbed the motion of Uranus. Precisely at that point, astronomers discovered Neptune.
However, the gravity of Neptune could not fully explain all the anomalies in the motion of Uranus. This is why scientists came up with a hypothesis about the existence of another planet beyond the orbit of Neptune. In 1915, Percival Lowell, the founder of Lowell Observatory, completed his calculations and reported at a meeting of the American Academy of Arts and Sciences on where to look for Planet X. After a thorough search, the planet was discovered on March 13, 1930 by Clyde Tombaugh, an observer at Lowell Observatory, exactly where Lowell predicted.
However, when Pluto’s mass was measured, it proved to be less than Lowell’s estimate (the difference was so large that in 2006 Pluto was denied the right to be called a planet; now it is a dwarf planet). Pluto was moving in a completely different orbit than the one calculated for it. The calculations were formally correct; the error lied in the initial conditions because Lowell used the wrong mass. Nevertheless, Pluto was found where it was predicted. Scientists had to admit that discovery was an incredible event in terms of probabilities. Pluto fortuitously happened to be in the sky close to the point calculated by the scientist!

A similar story happened with the discovery of the Higgs boson. The British physicist Peter Higgs published in the 1960s an article where he described an elementary particle whose existence explains the origin of the mass of particles. In 2012, this particle was discovered in experiments at the Large Hadron Collider, and its properties turned out to be exactly as predicted by the theory.

Zwicky’s method of directed intuition

So, it follows from the above that not all discoveries are unpredictable. On the contrary, most of them not only could but also should have been predicted.

No theory exists yet about how to predict discoveries, but researchers can apply some rules-of-thumb in order to foresee, to some extent, the outcome of their experimental or theoretical work. These rules have been established and described, e. g., the use of morphological analysis to scrutinize all conceivable implications of a theory being proposed.

DISCOVERIES OF THE 4TH CLASS had been predicted. Examples are the discovery of background radiation, X-ray pulsars, the curvature of light rays near the Sun, gravitational radiation from the mergers of black holes, quantum entanglement, Higgs boson

In the early 1930s, Zwicky came up with a morphological method, which he called the method of directed intuition. This method forces the researcher to see not only the habitual path but also all possible options. Zwicky suggested the researcher should take a sheet of paper and draw a morphological table where one axis represents the main parameters of the future theory (mechanism, structure, or phenomenon) and the other one represents the possible values of these parameters.

Much later, he wrote about that in his book Morphological Astronomy, published in 1957. In 1971, Zwicky visited Moscow and gave a lecture at Moscow State University, where he spoke about the discovery of neutron stars:

“As the main parameter for one of the axes of the morphological box, I took the characteristic size of a star. This size is a combination of the world constants: the Planck constant, gravitational constant, speed of light, proton mass, electron mass and charge. Let’s assume the largest possible combination relates to giant stars. The second largest combination of the constants is twenty times smaller. Let’s assume it relates to dwarf stars such as our Sun. The next characteristic size is smaller by another three orders of magnitude. On a stellar scale, it relates to the size of white dwarfs, about ten thousand kilometers.

“As a rule, researchers stop right here. But let’s put aside the inertia. We need to get rid of the psychological inertia in our ideas about the size of stars. So, we overcome ourselves and move on. The next combination of the constants gives a characteristic size several hundred times smaller than the previous one. What is this, a star several kilometers in size?! The first thing I want to say, ‘That’s impossible!’ But we must make ourselves forget this word. Let it be possible. What is this star? Let’s calculate its density. Divide a mass equal to the solar mass by the volume of a sphere of one-kilometer radius. We get an incredible value: a hundred billion tons in one cubic centimeter!

This well-known anecdote is a great example of how psychological inertia may hinder one’s ability to see all possible variants of a phenomenon:
The famous German microbiologist Robert Koch was busy working in his laboratory near a vessel shrouded in steam and smoke. His assistant entered the room.
“Could you guess,” Koch asked him, “what’s being cooked here?”
The assistant named all the bacteria he knew, but Koch kept shaking his head. When the assistant gave up, Koch exclaimed laughingly:
“Those are sausages!”

“Ordinary matter of atomic nuclei and electrons cannot exist at such a density. Electric repulsive forces do not allow it. We need neutral particles. We know them: these are neutrons. The star is made of neutrons tightly pressed together. But in order to compress a star to such a huge density – ​our psychological inertia objects – ​it is necessary to do an enormous amount of work against the forces of gravity, to compensate for the potential energy of gravity. For a neutron star, this potential energy is about 10⁵³ erg. But… exactly this energy is released in a supernova explosion! Here is the solution. Yes, neutron stars can exist. Moreover, no other stars except neutron ones (giants, ordinary and white dwarfs) can explain such a huge release of energy in a burst.

“Fine. Now we can stop and think again over this idea, which we have obtained by the method of directed intuition. But… have we filled all the cells? No, there is yet another characteristic size, another combination of the world constants, eighteen orders of magnitude smaller than the previous one! This size relates to a star with a radius of… 10^–13 cm. The size of an electron. A star compressed almost to a point. Can we possibly call such objects stars? If they are stars, they are truly infernal ones…”

This was the first application of morphological analysis. Even a simplest box containing only one axis yielded two correct predictions. Two discoveries. But what if Zwicky and his colleague Baade had acted by trial-and-error?

A great example of combining trial-and-error with psychological inertia is Kepler’s law, i. e., the planets move in ellipses, with the Sun at one of the foci of the ellipse. A German mathematician, astronomer, and mechanic, born in the second half of the 16th century, Kepler was an immensely hardworking man and one of the most outstanding minds of his time. Back then, it took a man a lot of courage to be a supporter of Copernicus. Yes, Kepler was brave, but he could not renounce the inertia that arose from his aesthetic ideas about nature. Nature, as Kepler believed, seeks harmony (more precisely, God, who created nature, made it harmonious – ​that is beyond doubt). Therefore, the planets must also revolve around the Sun in circles, the most harmonious of all shapes.

Kepler could not step aside from this idea for years. Describing planetary orbits, he searched through all possible combinations of circles and spheres. But he did not obtain an agreement with the observations and realized that no combination of circles could explain the discrepancy of 8 arc minutes between the predicted and observed motion of Mars.

It took Kepler time and effort to get on the right track. It is unlikely that anyone in his place would have abandoned the idea of circles and would have dared to search in a different direction. Until the end of his life, Galileo did not accept Kepler’s idea that the planets’ orbits differ from the circle! But Kepler nevertheless overstepped the internal prohibition. If he had known the morphological method, he would have constructed an axis of possible geometric shapes with no angles, which would have included an ellipse. But Kepler tried and, of course, committed an error. At first, he decided that the planets move around the Sun in egg-like ovals. Only after realizing that he had made another mistake, he paid attention to the ellipse.

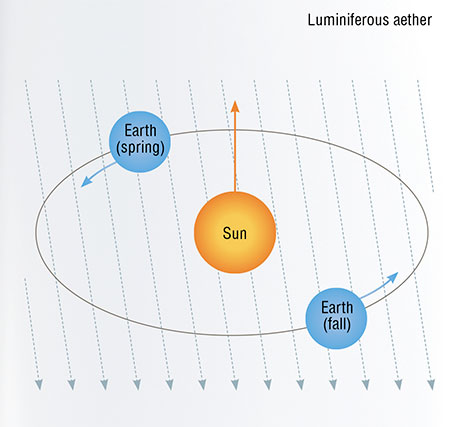Could morphological analysis have predicted the discovery made in 1881 by Michelson? Let’s construct a morphological table for light as an object. Michelson was specifically interested in the speed of an electromagnetic wave. He could, in fact, have drawn this single axis. Here are the options – ​the speed of light in a given reference frame is either constant or variable. But there are two reference frames here, one of which Michelson associated with the Earth and the other with the hypothetical ether. What options arise? The speed of light is different in the two frames of reference; it is the same in both frames; it is variable in one frame and constant in the other; it is variable in both frames. There are no other options. Among the options listed, you do see the result of Michelson’s experiment, i. e., the speed of light is the same in both frames of reference.

The options in real-life problems are not two or three in number; there are tens, even hundreds, of them, and sorting through them, even systematically, may take a lot of time and effort. Lastly, one cannot know in advance which particular cell of the morphological table contains the target prediction. The six fundamentally possible results of Michelson’s experiment could be foreseen through morphological analysis. Only one of the six options could be true, and it proved to be. But could Michelson say in advance which one?

Morphological analysis in its current form is only the first attempt at systematization. The main disadvantage of the method is that it leaves the selection of the right idea to chance. In order to find the right solution, you need to look through all the cells.

There is more to it. Of course, constructing morphological tables unchains one’s imagination and loosens psychological inertia, but not by much. In any case, there is no guarantee that the entire field of trial and error will not be covered by a network of cells. True, the researcher no longer has to rush around chaotically, grabbing at the nearest solution and exclaiming, “What if!” Nevertheless, even if the researcher has sorted through the options systematically, he or she may still let the goldfish, i. e., the discovery, slip through the net, because the latter is shorter and narrower than it should be.

Nevertheless, morphological analysis allowed Zwicky to predict the discovery of neutron stars and black holes. A similar analysis allowed me in 1971 to predict the discovery of background gravitational waves. At that time, the Big Bang theory had not appeared yet, and only a few years had passed since the discovery of the cosmic microwave background radiation (a second-­class discovery). The question arose: Is electromagnetic radiation the only type of radiation that could have arisen in the first years after the Big Bang? The morphological box in this case is very small, i. e., only one axis.

Here is a quote from my article published in the journal Znanie – ​sila (‘Knowledge Is Power’) in 1971: “Let us draw up the axis of the possible emitters. Let us put the Universe first. Yes, at an early stage of development, the superdense body of the Universe could have been emitting gravitational waves. Now these waves have stretched over many parsecs. And here is another prediction – ​we will discover BACKGROUND gravitational radiation, whose source was the Universe in the early periods of expansion.”

In reality, the Soviet physicist Leonid Grishchuk was the first to write (in 1977) about the possibility of existence of background gravitational waves.

Altshuller’s method of fantograms

Another method for predicting scientific discoveries, i. e., the so-called fantogram method (a development of morphological analysis), was proposed by the Soviet science fiction writer and inventor Genrikh Altshuller, the author of TRIZ (Theory of Inventive Problem Solving).

The fantogram is a morphological table supplemented by an axis of parameter changes. Morphological analysis allows one to generalize and systematize everything one knows about plants. Or about neutron stars. Or stars in general. A fantogram also describes what is possible but has not been realized. It also describes what does not exist in reality but emerges in imagination. And sometimes even what is difficult to imagine.

TRIZ recommends using fantograms to develop creative imagination. But the scientist’s subconscious mind has long mastered this method. The fantogram cells – ​is it not them that the scientist sees in a dream or on a walk, when he or she does not seem to be thinking about the problem at all? Isn’t that why the solutions that arise at the most unexpected times are so paradoxical and so very often absolutely correct?

The goal, however, is not to wait for an insight but to consciously change by known techniques the object of research, the law of nature, the phenomenon, the proof. As a rule, the same psychological inertia cuts in. The fantogram is a mixture of the real and the fantastic, and what scientist would choose to rely upon a fantastic idea rather than a proven logical scheme?

Recall Zwicky. He found neutron stars in his morphological table. In fact, it was one of the cells in a fantogram. Zwicky took one of the properties of a star – ​its size – ​and used the reduction technique.

However, one does not need to change all the cells in the morphological box, only those ones that create a contradiction. To find a contradiction means to set a scientific problem. To use a fantogram means to bring the solution much closer.

After all, Zwicky was changing not an arbitrary parameter of the star but the one containing a contradiction. A supernova explosion requires energy. An ordinary star does not have that energy. Here lies the contradiction; i. e., there is energy for supernova explosions (we see the bursts!) but not in ordinary stars. To resolve the contradiction, we need to know what energy goes into the energy of the burst. Gravitational energy, as Zwicky suggested. The gravitational energy of a star depends on its size. Then, the initial contradiction transforms into the following one: colossal gravitational energy is released in a supernova explosion (we see the burst), but there is no such energy in an ordinary star (the size is too large).

We have a contradiction between observation and interpretation. Zwicky changed the interpretation and predicted the discovery of neutron stars.

Einstein did not use morphological analysis; before he formulated the principle of equivalence, he did not publish a single erroneous work on the theory of gravity.

The end of the 19th and beginning of the 20th century saw many hypotheses proposed to save Newton’s theory of gravity. There were plenty of errors. Einstein set out to solve this problem and found a grain of truth. Did he find it straightaway? No, he did not. His discovery was preceded by years of reflection on the problem of gravity. By years of mental trials. And errors, of course.

The process of thinking resembles an iceberg, and the wiser the scientist, the deeper the underwater portion of that iceberg goes. What stays above the water – ​what the scientist himself calls the work of thought – ​is the work of the conscious mind. But deep down under the surface, secretly from everyone and even from the scientist himself, unconscious work is underway, i. e., subconscious enumeration of options or an unconscious process of solving the problem.

Psychological inertia, which we have not yet learned to overcome, does not allow our conscious mind to go crazy and keeps it within the boundaries of common sense. This is why it is so difficult for our mind to find a solution, which often looks impossible. It seems that the subconscious mind does not have this brake lever. It just plays with distant associations, with incredible allegories and analogies, and then a sudden association or analogy strikes into this invisible subconscious game and prompts a solution.

This is why insights so frequently arrive “in a dream” or “on a walk.” The illogicality of dreams has nothing to do with the logic of science. This is what distinguishes a brilliant idea from an ordinary one. Only later, having found the right solution, which has popped up as if from nowhere, you can build a bridge of logic, a road from the old idea to the new one. The subconscious mind tries different options, and the intuition selects the right one. The role of intuition lies with the choice, but in order to choose, you first need to have something to choose from.

Therefore, when we talk about Einstein, we do not refute the trial and error method. We stress the yet unexplored role of the subconscious mind.

The subconscious work is hidden from view, and the scientist himself often believes that he simply guessed the right law. The very method of predicting laws boils down to guessing correctly. The famous American physicist Richard Feynman wrote: “The method of guessing the equation seems to be a pretty effective way of guessing new laws.” And then he explained his thought: “In general we look for a new law by the following process. First we guess it… To guess what to keep and what to throw away takes considerable skill. Actually, it probably is merely a matter of luck. But it looks like it takes considerable skill.”

A weird thing to say, isn’t it? To say that new laws need to be guessed is to say that everything is decided by a lottery. If you do not guess, someone else will. If you try and fail, someone else will try too and hit the mark. Why then does a genius hit the mark more often?

We need to try and grope for a system. Morphological analysis is the first step towards the methodology of discoveries and scientific inventions. It allows you to consciously do what the subconscious mind usually does. But there must be some other method of choice! The subconscious is the source of the most interesting and promising ideas, which “emerge” from it. These ideas are often true. How can one consciously select such ideas from the morphological box? How can one consciously find the right idea from a much larger number of cells in a fantogram?

For inventions (including those related to science), this problem is now successfully solved by TRIZ. Its methods also help inventors make discoveries, but only those of the fourth and third class. For such discoveries, TRIZ offers a well-developed “research field,” i. e., the cells of morphological boxes and fantograms.

The situation with discoveries of the first and second class is much more difficult. To make such a discovery, a scientist must have an extremely developed creative imagination and a lack of psychological inertia. The methodology for developing creative fantasy exists and shows good results. But that is another story and a topic for another article.

References

Altshuller G. S. Tvorchestvo kak tochnaya nauka, Moscow: Sov. Radio, 1979 [in Russian]. – Altshuller G. S. Creativity as an Exact Science, CRC Press, 1984.

Altshuller G. S. Naiti ideyu (To Find an Idea), Novosibirsk: Nauka, 1986 [in Russian].

Amnuel P. R., Guseinov O. Kh. X-ray emission on accretion of interstellar matter by neutron stars // Izv. Akad. Nauk Azerb. SSR, Jan. 1968 [in Russsian].

Amnuel P. R. Discoveries that we choose // Znanie – sila. 1971. N. 8 [in Russian].

Amnuel P. R. Dalekie mayaki Vselennoi (Distant Beacons of the Universe), Fryazino: Vek-2, 2007; 2nd ed.: DMK+Vek-2, 2022 [in Russian].

Vilenkin A. Mir mnogikh mirov (A World of Many Worlds), Moscow: Astrel, 2009 [in Russian].

Shklovsky I. S. Supernovae (Physics & Astronomical Monograph), Wiley, 1968.

Baade W., Zwicky F. On Super-Novae // Proc. National Acad. Sci. 1934. V. 20(5). P. 254–259.

Feynman R. The Character of Physical Law. N. Y.: Modern Library, 1965.

Zwicky F. Morphological Astronomy. Berlin: Springer-Verlag, 1957.